오랫만에 자료구조 시간으로 돌아왔습니다. heap 자료구조는 다들 익숙하실 겁니다. 그리고 힙을 build 하는 연산을 힙 사이즈가 n이라면 O(n)에 할 수 있다는 이야기는 예전부터 들어왔어요. 그런데 어떤 원리로 그것을 할 수 있을까요? 자바에도 PriorityQueue가 있으니, 이 클래스의 내부 소스를 까보면서 이야기 해 보도록 하겠습니다.
문제 상황은 임의의 순서로 배열되어 있는 array를 heap 조건에 맞추어서 build 하는 것입니다.
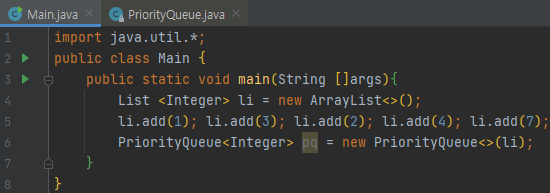
그에 맞게 코드를 짜 보았습니다. PriorityQueue에 list를 넘겨주었는데요. Collection을 받았기 때문에, 아래 메서드가 호출될 겁니다. 아래에 나와있는 코드를 보겠습니다.

여기서 보면 List는 SortedSet도 아니고, PriorityQueue도 아닙니다. 그냥 Collection일 뿐입니다. 따라서 201번째 줄의 else 절에 걸릴 겁니다. 그러면 아래의 메서드가 호출됩니다.

이 메서드는 2개의 메서드를 호출합니다. 하나는 initElementsFromCollection입니다. 다른 하나는 heapify인데요. 하나 하나 보겠습니다.

먼저, initElementsFromCollection은 별 게 없어 보입니다. 단지, len개 만큼의 loop가 돌아갈 뿐입니다. c의 초기 크기가 n이였다면, 시간 복잡도는 대략 O(n)이 됩니다.

다음에 heapify를 보면 size/2 - 1부터 0까지 siftdown을 돌리는 것을 볼 수 있어요.

Integer는 (comparator가 구현되어 있지 않았고) comparable 하기 때문에 689번째 줄이 호출되는데요.

k < half일 때 까지 while loop를 돌립니다. 정리하면 siftDown은 i번째에 있는 수를 heap의 성질을 만족하는 올바른 위치까지 내려버리는 함수라고 할 수 있어요. 이 while loop 하나 도는 것을 단위 연산 하나로 칩시다. 그러면, 제가 잡은 단위 연산은 무엇을 의미하나요?
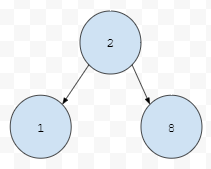
현재 기준 위치에 2가 있어요. 그리고 이들의 자식이 1, 8이라 해 보겠습니다. 우리는 최솟값의 우선 순위가 높은 우선순위 큐를 build 해야 해요. 그런데, 2가 1보다 우선 순위가 낮은데 부모에 있어요. 그러면 어떻게 해야 할까요?

자식들 중, 우선 순위가 높은 것은 1입니다. 1이 8보다는 작기 때문이에요. 따라서 1과 2를 비교하는데, 1이 2보다 우선 순위가 높아요.

따라서 1과 2를 바꿉니다. 즉, 부모와 자식들간의 우선 순위들을 계산해서 필요하면 down 시키는 것을 1 단위 연산이라고 합니다.
그러면, heapify 복잡도는 어떻게 될까요? 제대로 동작할까요? 결론적으로 말하면 O(n)이고 제대로 동작합니다. 제가 출제한 문제 중에서 heap을 쓰는 문제가 있었는데요. 문제 없이 돌아갔습니다.

siftDown은 최악의 경우에 O(log(n))이 됩니다. 그러면 heapify 함수는 최악의 경우에 O(nlog(n))이 될 거 같은데, 사실 O(n)이면 됩니다. 왜일까요? siftDown의 총 횟수를 계산해 보면 쉽게 알 수 있습니다. 총계 분석이라고도 하는 듯 합니다. 대충 n = 2^h이라 하겠습니다. 그리고 h = 4라고 해 보겠습니다.

그러면, 노란색 노드들에 있는 수들은 많아봤자 1번, 군청색은 2번, 주황색은 3번의 연산이 일어날 겁니다. 즉, 2^(h-1)개는 1번, 2^(h-2)개는 2번, ... , 2^(h-h)개는 h번의 연산이 일어나게 됩니다. 즉, 2^(h-i)개의 노드에 대해서, 단위 연산이 i번이 일어난다는 것입니다. 이를 다시 도식화를 시켜 보겠습니다.
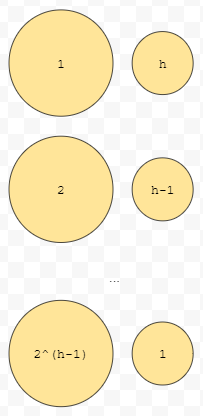
요런 식으로 나오는데요. 가로 방향의 1과 h, 2와 h-1 등은 두 수를 곱해야 한다는 의미이고요. 이 결과들을 합한 결과를 구하는 것이 목표입니다. 오른쪽에 있는 1, 2, ... , h를 잘 보면 어떻게 정리해야 하는지 힌트를 얻을 수 있어요.

결국, 저 상황은 (1 + ... + 2^(h-1))의 결과 값과, (1 + ... + 2^(h-2))의 결과 값과, ... , 1의 결과 값을 모두 더하는 것과 같아요. (1 + ... + 2^(h-1))은 2^h보다는 작고, (1 + ... + 2^(h-2))는 2^(h-1)보다 작고, ... , 1은 2보다 작습니다. 그리고 0은 1보다는 작으므로, 최종 결과값은 2^(h+1)보다는 작습니다. 우리는 n = 2^h라고 했으므로, 최종 결과값은 2n보다 작게 됩니다. 이 값은 최악의 경우에, 단위 연산이 몇 번 일어나는가였습니다.
그런데 단위 연산은 잘 보면 별 게 없었어요. 그냥 자식 둘을 비교한 다음에, 우선순위가 더 높은 쪽과 부모를 비교합니다. 만약에 자식이 우선순위가 더 높으면 바꿔버리면 되었습니다. compare 2번, 대입 연산 2 ~ 3번이 일어납니다. 이 둘을 상수로 칠 수 있으면, 단위 연산 또한 상수가 됩니다. 상수에 2n을 곱하면 O(n)이 됩니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| java linkedhashmap removeeldestentry 메소드에 대해 알아봅시다. (0) | 2023.04.04 |
|---|---|
| java stack 클래스와 대체해서 쓸 만한 arraydeque를 간단히 알아봅시다. (0) | 2023.02.28 |
| 펜윅 트리 (fenwick tree) : 구간합을 빠르게 구한다. (0) | 2021.03.14 |
| java map find key in value : 2개의 맵을 씁시다. (0) | 2021.01.28 |
| 스택계산기 구현 : 연산자 우선순위와 결합 순서만 생각해 봅시다. (2) | 2020.07.02 |


최근댓글