제가 개최한 2회 코딩 테스트는 1회 코딩 테스트와 비교했을 때 굉장히 어렵다는 의견이 많았습니다. 그 이유 중 하나는, 중간 정도였던 문제들의 까다로웠던 함정들 때문입니다. 가희와 btd5는 그런 면에서 골드 4였음에도 불구하고 상당히 까다로웠습니다. 체감 난이도는 1회 때의 가희와 로그 파일과 맞먹을 정도였으리라 추측됩니다만, 어디까지나 이건 제 추측일 뿐입니다. 거기에 5번은 철도 용어들이난무하다 보니 어질어질 했을 겁니다.
그러면 왜 체감 난이도가 높아졌는가에 대해 먼저 분석해 보겠습니다. 문제를 잘 읽어보시면 원점에서부터 공격 방향이 키워드임을 알 수 있습니다. 그리고 이것은 직선의 기울기와 매우 밀접한 관계가 있음을 알 수 있습니다. 여기까지 읽어보셨다면, 공격 방향의 x값과, 풍선 좌표의 x값이 0인 경우에만 예외 처리를 하면 되겠다. 라는 생각을 하실 수 있습니다. 즉, 기울기로만 처리를 합니다. 예를 들자면, 풍선 1의 좌표가 (2, 1)에 있고 풍선 2의 좌표가 (4, 2)에 있으면 원점과 풍선 1의 좌표를 잇는 직선의 기울기와 원점과 풍선 2를 잇는 직선의 기울기는 1/2로 같습니다.
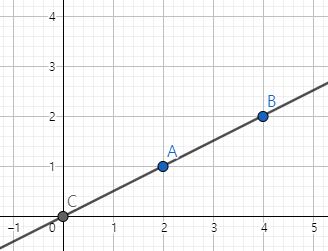
그래서, 다트 거너의 공격 방향이 (3, 6)이라면, 원점 (0, 0)과 (3, 6)을 잇는 직선의 기울기 또한 1/2이므로 A와 B가 모두 맞게 됩니다. 그런데, 만약에 방향이 (3, 6)이 아니라 (6, 5)였다면 어떨까요?
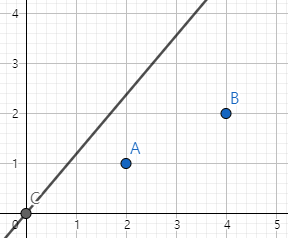
A와 B는 맞지 않습니다. 그래서, 공격 방향이 (x', y')이라면 y'/x'과 풍선들과 원점을 잇는 직선의 기울기가 y''/x''일 때, y''/x''과 y'/x'이 같은지 비교하는 로직을 작성하고, 케이스 처리만 잘 하시면 될 거라고 생각하실 수 있습니다. 문제는 y'', x'', y', x'이 모두 double형인 경우에 생길 수가 있어요.
풍선들의 좌표가 -10억 이상 10억 이하다라는 조건에서 간파를 하셨겠지만, y''/x''과 y'/x'의 차가 매우 작아지게끔 만들 수 있습니다. 대충 (n-1)/n 과 n/(n+1) 꼴인 데이터를 차례대로 넣어버리면 되는데요. 좌표의 절댓값 최대가 10억이므로, 풍선은 (10^9 - 2, 10^9 -1)에 있고 거너가 바라보고 있는 방향은 (10^9 - 1, 10^9) 이런 식으로 두면 차이가 매우 작아지게 만들 수 있습니다.
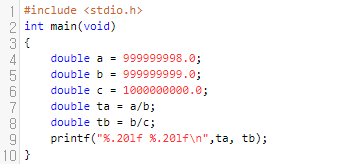
간단하게 프로그램을 작성해서 확인해 봅시다. a/b와 b/c의 값은 다릅니다. 그런데 출력 결과는 어떻게 될까요?
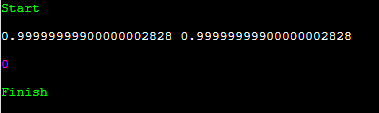
별로 다른 게 없어보입니다. 실제로 이 둘의 차이는 약 1/10^18 입니다.
그러면 double의 compare를 이용하면 소용이 없을까요? 네. 소용이 없습니다. 이펙티브 자바에서는 float나 double을 비교할 때에는 이 메서드를 이용하라고 하는데요? 그것은 정밀도를 어느 정도 포기했을 때 이야기입니다. 이 문제는 생각보다 정밀한 값을 요구하고 있습니다. double로도 처리가 안 되었다면, double로 처리할 수 있는 오차보다 더 세밀한 오차까지 컨트롤 할 수 있어야 한다는 의미입니다. 제가 말했던 테스트 케이스를 그대로 넣어보겠습니다.
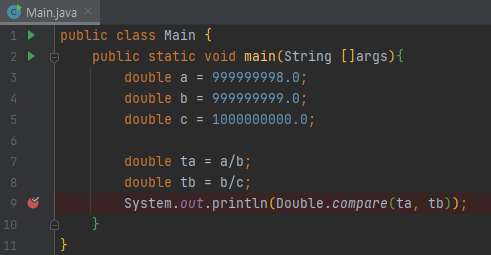
Double.compare로 a/b와 b/c의 값을 비교해 보겠습니다.
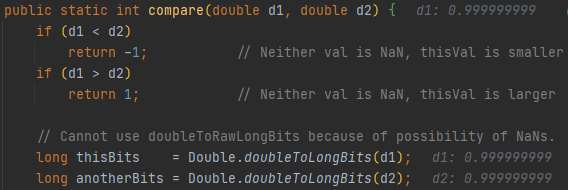
d1하고 d2가 같으면 thsiBits랑 anotherBits를 비교하게 되는데요.
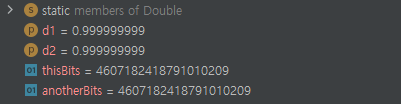
둘이 같네요? 같다고 판단해 버립니다. 실제로는 다른 값인 데도 말입니다. 그 이유 중 하나는 1/10^18은 1/2^52와 비교했을 때 한없이 작기 때문입니다. 어디서 얼핏 듣기로는 Java의 BigDecimal이 좋다고 하는데. 사실 이것도 답이 아닙니다. 왜냐하면 이것은 고정 소수점을 표현하기 위한 것이지, 순환 소수와 같은 것을 표현하는 것이 아니기 때문입니다.
그러면 어떻게 해야 할까요? 이 문제의 의도는 매우 간단합니다. 실수 오차에 대한 개념을 알고 벡터의 기본 연산인 정수배, 실수배 연산을 응용할 수 있는가였습니다. (1, 2)와 (2, 4)가 원점으로부터 같은 방향을 보고 있다는 거를 판단하기 위해서. 데이터 (2, 4)를 잘 봅시다. 2와 4의 최대 공약수인 2로 나누면 (1, 2)가 됩니다. (-1, -2)와 (-2, -4)는 어떨까요? -2와 -4의 절댓값은 각각 2와 4입니다. 2와 4의 최대 공약수는 2입니다. 따라서 -2를 2로 나누고 -4를 2로 나누면 (-1, -2)가 되는데 이것은 (-1, -2)와 같습니다. 로직을 보겠습니다.

먼저, gcd는 우리가 알고 있는 것과 크게 다르지 않습니다. x >= y >= 0이고 x, y 둘 다 0이 아닌 케이스만 들어온다면 y가 0일 때 x는 0보다 큰 정수이므로 gcd 값은 x를 리턴해 주면 됩니다. 문제는 x가 y의 배수일 때 왜 y를 리턴 안 해 주었냐는 건데요. x가 y의 배수라면 12번째 줄에서 y값이 들어가고 x%y가 0일 겁니다. gcd(y, 0)의 값은 y이므로 따로 넣지는 않았습니다.
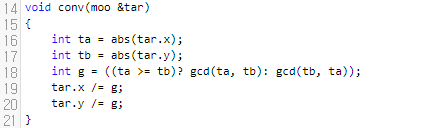
중요한 건 이 부분입니다. tar에는 풍선이나 거너의 공격 방향이 들어 있는데요. 16 ~ 17번째 줄을 보면, tar.x와 tar.y의 절댓값을 가지고 와서 이들의 최대 공약수를 18번째 줄에서 구하고 있어요. 다음에, 원래 들어온 공격 방향의 x값과 y값을 각각 g로 나누는데요. 이는 벡터에서 k배를 해 봤자 크기만 바뀌지 방향이 바뀌지는 않기 때문입니다.
방향이 같다면 벡터의 크기만 통일 시켜준다면 손쉽게 비교할 수 있다는 것을 역이용 한 것입니다.

그러면, 방향 비교는 어떻게 하면 될까요? 간단합니다. 같은 방향의 벡터에 대해서 크기가 통일되었기 때문에, conv를 한 결과를 가지고 x값과 y값이 같은지만 비교해 주면 됩니다.

테스트 케이스로 잘 동작하는지 확인해 봅시다. 각각 1, 1, 0, 0, 0이 나와야 합니다.

잘 나옴을 알 수 있습니다.
'구현' 카테고리의 다른 글
| 가희와 키워드 : equal 연산이 들어오면 hash 계열 구조를 이용해 봅시다. (0) | 2022.02.25 |
|---|---|
| 가희와 자원 놀이 : 자원 카드를 어떻게 관리할지 생각해 봅시다. (0) | 2022.02.14 |
| 하드 코딩을 이용해서 7 세그먼트 구현 응용 문제를 풀어봅시다. (0) | 2021.09.15 |
| 가희배 코테에 나온 수인분당선 문제를 세팅한 이야기 (5) | 2021.09.12 |
| bounding box를 이용해서 가희와 거북이 인형을 풀어봅시다. (0) | 2021.08.31 |


최근댓글