RSA 알고리즘은 어디선가 많이 들어보셨으리라 생각이 듭니다. 어떠한 메세지가 있습니다.

메세지 M을 a1이라는 key로 암호화 했습니다. 암호화 된 메세지를 E(M)이라고 하겠습니다.
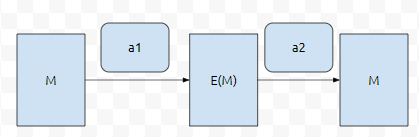
이를 a1과 다른 값을 가지는 a2로 복호화를 합니다. 예를 들어, 3으로 암호화를 시키고 5라는 키로 복호화를 시키는 식입니다. 비대칭키 알고리즘인 셈입니다.
이 포스팅에서는 과정만 보일 겁니다. 그러니 오일러 파이나, CRT와 같은 용어는, 천천히 알아가시는 것도 좋을 듯 싶습니다. 다만, 제가 중간 중간 보라색으로 칠한 부분은 심도 있게 생각해 보셔도 좋을 듯 싶습니다. 먼저, 두 소수의 곱으로 이루어진 합성수를 생각해 보도록 하겠습니다. 예를 들어 3과 5를 곱해서 나오는, 15라던지, 37과 41의 곱으로 이루어진 1517을 생각해 보겠습니다.
일단, 암호화 과정을 그림으로 그리면 아래와 같습니다.
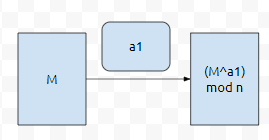
여기서 n은 서로 다른 두 소수를 곱한 pq입니다. p = 37, q = 41이라 하겠습니다. 그러면 n은 1517이 됩니다. 그러면, 암호화를 사용되는 데 이용할 키 a1은 어떻게 구하는 게 좋을까요? (p-1)(q-1)의 값인 1440과 서로소이면서 1보다 크고, (p-1)(q-1)보다 작은 값 중 하나를 선택해 보겠습니다. 대충 a1의 값을 31로 잡아보겠습니다.

다음에 a2 값을 구해야 하는데요. 이 값을 어떻게 잡을까요? 31과 a2를 곱한 값이, (p-1)(q-1)의 값인 1440으로 나누었을 때 나머지가 1이 나오는 값을 찾으면 됩니다.

이는 간단하게 프로그램으로 구현할 수 있습니다.

이 중에 하나인 1951로 복호화를 하면 되겠군요.
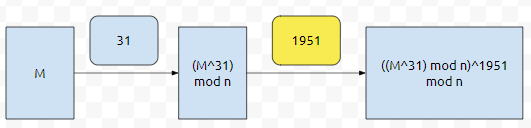
31로 암호화를 하고, 1951로 복호화를 하면, 신기하게도 M이 나옵니다. 일단 첫 번째 질문, a1을 알 때, a2를 어떻게 빨리 구할까요? 우리는 암호화를 할 때 쓰였던 키 값인 a1을 알고 있습니다. 단지 a2를 모르는 상황인데요. 이를 x라고 두겠습니다. 그러면, 아래와 같이 쓸 수 있습니다.

뭔가 익숙한 꼴이 보입니다. ax + by = C꼴입니다. 초록색으로 칠해진 것들은 이미 알려진 값들입니다. 이 꼴은 확장 유클리드 알고리즘을 이용하면 꽤 빠르게 구할 수 있습니다.
그러면 이것이 성립할까요? 우리는 아래를 증명해야 합니다. 암호화 할 때 e (=a1), 복호화 할 때 d (=a2)가 쓰였다고 하겠습니다. 그리고 M은 n보다는 작은 수라고 해 보겠습니다.

우리는 이것이 성립합을 증명해야 합니다. 우리가 알고 있는 사실은 ed를 (p-1)(q-1)으로 나눈 나머지는 1이라는 것입니다. 이 사실을 이용해서 수식을 변형해 보겠습니다.
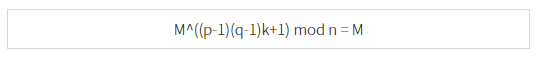
아직은 뭔가 보이지 않네요. 그런데 우리에게 알려진 정보가 몇 가지 더 있습니다. 바로 p와 q는 소수라는 것입니다. 그러면, 아래 두 개가 성립합니다.

p와 q가 소수이니 위 두 수식은 성립합니다. 이것을 이용해서 p에 대해서 모듈러를 취해 보고, q에 대해서 모듈러를 취해 보도록 하겠습니다.

먼저, M^(p-1)에 걸린 지수 부분을 보면, (q-1)k입니다. 제가 주황색으로 칠한 부분입니다. 그런데, M^(p-1)을 p로 나눈 나머지는 1입니다. 1을 100만번 곱해도 1입니다. 따라서, M^(ed)를 p로 나눈 나머지는 M을 p로 나눈 나머지와 같습니다.

마찬가지 방법으로 q에 대해서 모듈러를 취해도, M mod q와 같습니다. 어떠한 수 K가 있습니다. K가 있는데, K를 p로 나누었더니, r이 나오고, K를 q로 나누었더니, 이것도 r이 나왔습니다. 당연하게도, r은 p, q보다는 작은 수입니다. 그러면 K를 pq로 나눈 나머지는 어떻게 될까요? p와 q가 서로 다른 값을 가지는 소수임에 주목을 해 봅시다. 그러면, gcd(p,q)의 값은 1이 나옵니다.
그러면, px를 q로 나눈 나머지는 어떻게 나올까요? px를 q로 나눈 나머지가 r이라면, px = qy + r꼴로 표현할 수 있습니다. r은 1의 배수이므로, r이 q보다 작은 정수라면, px = qy + r을 만족하는 (x,y)쌍이 존재합니다.

어찌 되었던 해는 있다는 이야기입니다. 그리고, px를 q로 나눈 나머지가 0, 1, ... , q-1인 경우가 모두 존재하고, 0을 q로 나눈 나머지와 pq를 q로 나눈 나머지는 0입니다. 주기가 q가 아니라고 해 보겠습니다. 만약에, x가 (0,q)에 속하는 정수이고, px를 q로 나눈 나머지가 0이라고 해 봅시다. 그러면, 몇 개의 수는 방문을 하지 않았을 겁니다.

만약에 pt를 q로 나눈 나머지가 0이였습니다. t는 0보다 크고, q보다 작은 정수였습니다. q개보다는 적게 돌았기 때문에, 0, ... , q-1 중에서 방문하지 않은 것이 있을 겁니다. 그 중 하나가 1이였다고 해 봅시다. 이는 0에서 출발했을 때, 1로 가는 경로가 존재하지 않는다는 의미입니다.
px를 q로 나눈 나머지 값이 0부터 q-1까지 모두 나올 수 있다. 그리고 0과 pq를 q로 나눈 나머지가 0이라는 의미는 px mod q가 q를 주기로 돌고 있다는 것을 의미합니다. 어떤 수를 p로 나누었을 때 나머지가 a이고, q로 나누었을 때 나머지가 b였다고 해 보겠습니다. 그러면, (px + a) mod q가 q를 주기로 도느냐가 문제인 건데요. a mod q = (pq + a) mod q = a로 같습니다. (px + a) mod q의 값은 아래와 같이 따로 뺄 수 있습니다.

a mod q는 상수이므로, (px + a) mod q 또한 q를 주기로 돌아버립니다. 즉, p로 나누었을 때 나머지가 a이고, q로 나누었을 때 나머지가 b이면서, 0보다 크거나 같고 pq보다 작은 정수는 하나만 존재합니다. M을 p로 나눈 나머지는 M mod p, M을 q로 나눈 나머지는 M mod q입니다. M은 n = pq보다 작은 수입니다.
따라서, M^(de)를 n으로 나눈 나머지는 M입니다. 그러면, 이게 맞는지 프로그램으로 확인을 해 보겠습니다.
d값이 31, e값이 1951이였습니다. n이 1517이였고요. de의 값은 60481입니다. M의 값을 0부터 256까지 변화시키면서 M의 값과, M^60481을 1517로 나눈 값이 같은지 확인해 보겠습니다.

i값과 i^60481의 값이 다르면 !을 출력하겠습니다. N은 서로 다른 두 소수의 곱으로 이루어진 값입니다.

출력 결과는 아무것도 없습니다. 단지, 0이 리턴되었다는 것만 나왔을 뿐입니다. 다음 시간에 이어서 해 보도록 하겠습니다.
'네트워크' 카테고리의 다른 글
| path traversal 공격 : 사용자의 입력을 믿으면 어떻게 될까요? (2) | 2021.04.21 |
|---|---|
| 인증 인가에 대해서 알아봅시다. (2) | 2021.04.16 |
| ip 주소의 netmask는 무엇일까요? (0) | 2020.06.21 |
| telnet과 ssh가 어떻게 패킷을 날리는지 간단하게 실습해 봅시다. (6) | 2020.06.15 |
| redirect vs forward : 새로 요청을 보내는가? (2) | 2020.04.17 |


최근댓글