sqrt를 어떻게 계산하면 좋을까요? 사실 어셈블리 명령에 fsqrt가 있긴 합니다. 그리고 추후에, 오늘 설명한 방법하고 Compare를 해 볼 겁니다. 우리는 sqrt(k)의 값을 구하는 것이 목표입니다. 어떻게 하면 좋을까요?
2차 방정식을 생각해 봅시다.

위 그래프는 f(x) = x^2 - 2의 그래프입니다. f(x)와 x축이 만나는 두 점을 (a,0), (b,0)이라고 둡시다. a<b라면, a는 -sqrt(2)이고 b는 sqrt(2)일 겁니다. 잘 보면, f(x)와 x축이 만난다는 것은 f(x) = 0이라는 말과 같은데요. 방정식 x^2 - 2 = 0을 푸는 것과 같기 때문입니다. 그런가요? x^2 = 2인 두 근은 어떻게 나오나요? x의 값은 root(2)이거나, -root(2)일 겁니다.

그러면, f(x) = x^2 - 3이라면 어떨까요? x^2 - 3 = 0의 두 근은 +root(3), -root(3)일 겁니다.
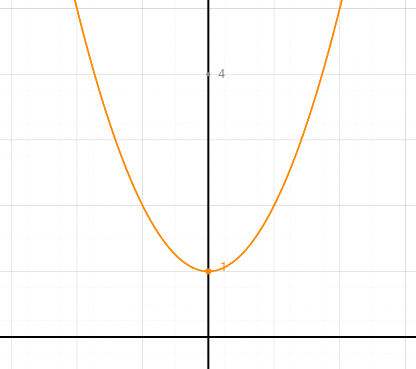
만약에 f(x) = x^2 + 1이라면 어떤가요? f(x)와 x축이 만나나요? 만나지 않습니다. x^2은 x가 R에 속해 있다면, 0보다 크거나 같기 때문에, x^2 + 1은 1보다 크거나 같을 겁니다. 1은 0보다 큽니다. 따라서, x^2 + 1 = 0을 만족하는 실근이 존재하지 않습니다. 허근 2개는 존재하겠죠. +i와 -i. 이 세 그래프를 왜 꺼냈을까요?
sqrt(k)는, f(x) = x^2 - k = 0의 근이 된다는 것입니다.
그러면, 이걸 어떻게 구할 건가요? 라고 물어보신다면, 아래와 같은 일을 계속 할 거에요. 먼저, 시작 x의 위치를 잡습니다. 예를 들어 root(3)을 구하기 위해서, f(x) = x^2 - 3을 그렸습니다. 그리고 x = 3에서부터 시작할 거에요. 그러면 먼저, y = f(x)와 점 (3, f(3))과 접하는 직선 L(1)을 구합니다.
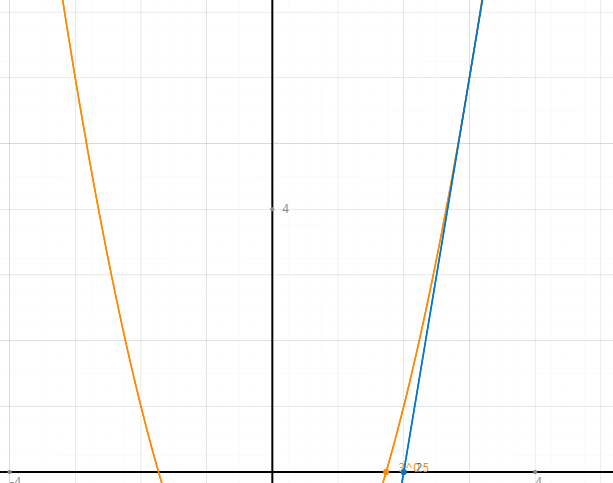
즉, 그림에서 파란 선을 구합니다. (3,6)을 지나고, x^2 - 3과 접한다. f(x)의 도함수 f'(x)는 2x이니까, (3,6)에서 접하는 직선의 식은 g(x) = 6(x-3) + 6 = 6x - 12가 됩니다. 여기서, 이 g(x)의 x절편을 구할 건데요. x 절편은 x축과 만나는 점과 관련이 있어요. 주황색 선을 지워보겠습니다.

그러면 x 절편이 2인가요? 네. 다음 x는 2입니다. 여기서 어떻게 해야 할까요? y = x^2 - 3과 (2, f(2))에서 접하는 직선을 찾아야 합니다. 이건 어떻게 찾으면 될까요?

초록색 선을 찾으면 되는데요. f(2)의 값은 2^2 - 3 = 1입니다. 즉, (2,1)에서 접하는 L(2)를 찾아야 하는데요. f'(x)가 2x라고 했으니까, 기울기는 4일 겁니다. 따라서 직선 L(2)를 h(x)라고 하면, h(x) = 4(x-2) + 1이 됩니다. 이 직선의 x절편을 찾아 볼까요?

1.75입니다. 다음 x는 1.75가 됩니다. 아까보다 sqrt(3)에 가까워 졌습니다. 이것을 언제까지 해야 할까요? 기준 x 값을 t라고 합시다. 그러면, (t, f(t))와 접하는 직선 L을 생각할 수 있을 겁니다. 이 L의 x절편의 값을 t'이라고 합시다. t'과 t의 차이가 매우 작아질 때 까지 반복하시면 됩니다.
이걸 수식으로 표현해 봅시다. root(k)를 구하기 위해서, 우리는 f(x) = x^2 - k를 가지고 왔습니다. 기준 x값을 t라고 합시다.

그러면, t'의 값은 노란색으로 칠한 값과 같을 겁니다. 우리는 기준 x값을 토대로 t'의 값을 구했을 때, t와 t'의 차이가 매우 작을 때 까지 loop를 돌리면 됩니다. 이 방법의 정당성을 보이기 위해서, 아래로 볼록한 함수의 특징을 이용하시면 좋습니다. 이것은 조금만 더 생각을 해 보세요.

제가 위에서 설명한 것을 그대로 코드로 옮겨 놓았습니다. eps는 0.000000001로 잡아놓았는데요. 이보다 더 작게 잡으셔도 무난합니다. x의 값이 구해질 때 까지, 단위 연산의 횟수는 op와 같은데요. 이것이 어떻게 변하는지 간략하게 보도록 하겠습니다. k가 1^20 - 1일 때, 1^22 - 1일 때, 1^24 - 1일때. 이 세 경우를 보도록 합시다.
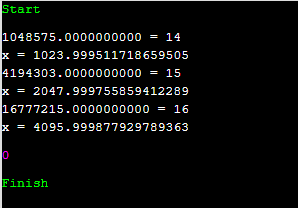
그러면 n이 4배로 커질 때 마다 대략, op의 횟수가 1씩 증가함을 볼 수 있어요. 2^20일 때 14번이면, 2^16일 때 12번, 2^12일 때에는 10번, 2^2일 때에는 5번. 그러면 대략 밑이 4인 log(n) + 5 정도로 볼 수 있습니다. 생각보다 빠르게 수렴한다는 것입니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| leetcode 898 bitwise ors of subarrays : 집합이 추가만 되는 상황을 생각해 봅시다. (8) | 2019.11.23 |
|---|---|
| leetcode 338 counting bits : 마지막 켜진 비트만 알면 된다. (6) | 2019.11.22 |
| 바이토닉 정렬 : 엇갈려 가면서 sorting 한다. (8) | 2019.11.02 |
| 피보나치 수열 : 왜 깡재귀로 구하면 지수 복잡도일까? (9) | 2019.10.30 |
| 그리디 알고리즘 : 매 순간 최적의 해를 선택한다. (6) | 2019.10.26 |


최근댓글