1년 6개월 전에 질문 글에 답변한 내용입니다. 그렇지만, java로 1325번 문제를 푸는 것과도 연관이 있으니, 잠깐 언급을 하도록 하겠습니다. 질문 글의 문제는, 많이 아시는 에라스토스 테네스 체의 구현체로 구현한 코드를 예제로 분석해 보겠습니다.

이 글의 흐름을 따라오기 위해서, 이 3가지만 쫓아오시면 충분합니다. (1) - (2)번은 링크의 Type of locality에 언급이 되어 있고, (3)은 spatical and temporal locality usage에 언급이 되어 있습니다. 그리고 그 주제의 2번째 단락에는, 해당 위치에 있는 데이터 값을 가지고 오면, 주변에 있는 것들도 cache에 같이 가져 온다는 언급이 되어 있습니다. 메모리의 계층도 같이 언급이 되어 있으니, 챙겨 보시면 도움이 될 듯 합니다.
제 컴퓨터에 장착되어있는 cpu에 대한 정보입니다.

L1은 6 x 32kbyte, L2는 6 x 256kbyte, L3은 9Mbyte입니다. L1, L2, L3에 대한 것을 모른다고 하더라도, 크기가 작다는 것을 알 수 있습니다. 당장 SDD도 TB 단위인데, L1을 보면 Kbyte 단위입니다. L2나 L3도 그렇게 크지 않습니다. 그런데, 이 문제를 풀려면, 대략 8M 정도의 수가 소수인지 아닌지에 대해서 저장을 해야 합니다. 이것을 홀수만 본다고 하면 4M개로 압축이 될 겁니다. 사실, 저는 이 방법으로 풀지는 않았고, 질문하신 분이 그렇게 푸셨습니다.

같은 알고리즘입니다. 맨 위는 long long형을, 중간은 int를, 아래는 bool형을 이용해서 4M개의 수가 소수인지 아닌지에 대해서 저장하였습니다. 이 3개의 자료형에 대해서 size는 잘 모르겠습니다만, 이 경우, 채점 결과를 보았을 때 크기는 bool < int < long long임을 알 수 있습니다.
이게 왜 시간 차이가 났을까요?
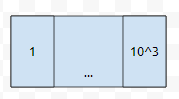
long long형으로 소수인지 아닌지를 관리했을 때, 한 번에 1000개의 원소를 긁어 온다고 해 보겠습니다. 이 단위를 블록이라 하겠습니다. 만약에 long long형 원소의 크기가 8byte라면, 4개의 블록을 저장할 수 있습니다.
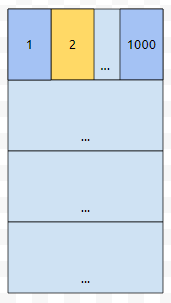
처음에 2에 접근했을 때, 1부터 1000까지를 올렸다고 해 보겠습니다. 이를 블록 1이라고 하겠습니다. 4에 접근할 때도, 6에 접근할 때도, 998에 접근할 때도, 이들은 블록 1에 속합니다. 블록 1은 캐시에 있습니다. 그러니, 그냥 cache에서 긁어오기만 하면 됩니다. 그런데, 1002에 접근하려고 하면 어떨까요?
이것은 블록 1에 속하지 않습니다. 2에 속합니다. 그러면 2에 있는지 봐야 겠는데. 없습니다. miss가 난 셈입니다.
그러면 어딘가에서 긁어 와야 합니다. 이 상황을 비유하면, 서류가 없어서 가까운 주민센터에 갔다 온 상황이 되어 버렸습니다. 여기까지 상황을 그림으로 정리해 보겠습니다.
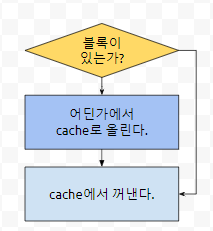
캐시 안에 해당 데이터가 있으면 그냥 꺼내오면 됩니다. 그게 없으면 군청색 부분을 추가로 수행하게 되는데, 기존에 캐시에 있는 것을 쓰는 것 보다는 오버헤드가 더 듭니다. 어딘가에서 가져 와야 하기 때문입니다.
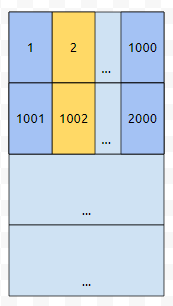
그런데, 하나 더 중요한 것은 cache의 크기가 그렇게 크지 않다는 것입니다. 그렇다면, 더 들어갈 자리가 없는 상황에서 cache miss가 난 경우에 없어져야 하는 블록이 생긴다는 의미입니다. 5002에 접근했다고 해 보겠습니다.
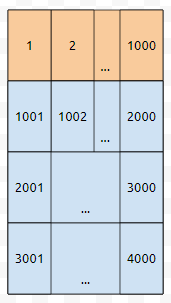
여기에서는 가장 오랫동안 접근하지 않은 블록을 제거하는 걸로 해 봅시다. 그러면 주황색으로 칠한 부분이 제거될 겁니다.

그리고 새로운 블록 5가 들어갈 겁니다. 한 블록 당 1000개의 데이터가 들어갔고, 400만개의 데이터를 저장해야 한다면, 우리는 1번부터 4000개의 블록을 써야 합니다. 2의 배수에 대해서만 소수가 아닌 것들을 마킹하는 과정에서는, 4000번 cache miss가 날 겁니다. 이는 당연한 것이, 처음에 캐시는 빈 상태였고, 2번부터 400만까지 2씩 건너 뛰면서 주루룩 보았기 때문입니다.

이 상황에서, 3부터, 3씩 건너 뛴다면 어떨까요? 1번 블록이 없는 상태이니 cache miss가 나올 거고, 순차적으로 보는데 2, 3, 4번 블록도 없으므로, 어디에선가 가져와야 합니다.

여기까지 언급한 내용을 그림 하나로 요약하면 위와 같습니다.
사용하는 메모리 공간이 줄었다는 이야기는, 단위 크기당 들어갈 수 있는 원소가 많아졌다는 이야기입니다. 예를 들자면, 한 블록에 1000개가 들어갔던 게 8000개나 들어간다던지. 그러면 어떻게 바뀔까요? 2의 배수만 돌릴 때만 보도록 하겠습니다.

처음에 2에 접근할 때, 1번부터 8000까지 저장되어 있는 블록을 올렸다고 해 보겠습니다. 8000도 블록 1에 속해있습니다. 그렇기 때문에, 8000에 저장되어 있는 값은 그냥 cache에 접근하면 됩니다. 하나 주목해야 할 점은 400만개의 수가 소수인지 아닌지 판단하기 위해서, 블록이 이전에는 4000개가 필요했다면, 지금은 단 500개만 필요하다는 것입니다.

즉 2의 배수에 대해서만 2부터 400만까지 돌았을 때, 이전에는 4000번의 miss가 났다면 지금은 단 500번밖에 안 난다는 것입니다. 이 말은 제 집에서 4000번 주민센터에 갔다 오느냐와, 500번 갔다 오느냐의 차이로 비유할 수 있습니다.

이 코드는, 한 블록당 BLOCK개의 수가 들어갔을 때, 얼마나 많이 캐시 미스가 나는지 출력합니다. 11번째 줄의 for loop는 에라스토스 테네스의 체 비슷하게 돌아가고 있고요. access 함수를 봅시다.

이것도 다른 것 없습니다. 블록은 최대 5000일 것이니, 블럭이 cache에 있는지 판단하기 위한 자료구조로 배열을 택해도 됩니다. 그리고, 그리고 가장 오래된 블록을 처리하기 위해서, cache라는 것을 queue로 구현하였습니다. 물론, lru 말고도 여러가지 알고리즘이 있습니다만, 코테에서도 나왔던 lru를 들고 왔습니다.
실행 결과는 어떨까요? 하나의 블록에 들어가는 원소 갯수가 1000일 때는 6767117, 8000일때는 999500이 나왔습니다. 800만까지 보아야 할 때에는 block에 들어가는 원소 갯수가 8000개일 때에는 2827000, 1000일 때에는 16305090이 나왔습니다. 이 차이가 얼마나 큰지, 다시 해당 문제에 대해서 제출해 보았습니다.

위에는 800만개짜리를 저장하기 위해서 long long을, 밑에는 char를 썼을 때 결과입니다. 260ms vs 92ms. 생각보다 꽤 크다는 것을 알 수 있습니다. 이는 배열의 덩치가 커짐으로 인해서, cache miss가 더 많이 일어났기 때문입니다.
'OS > 이론' 카테고리의 다른 글
| java arrayblockingqueue : 고정 크기를 가지는 생산자 소비자 문제에 써 봅시다. (2) | 2021.02.13 |
|---|---|
| java volatile : 변수의 가시성과 최적화 (2) | 2020.12.16 |
| java notify 메서드와 deadlock (0) | 2020.11.24 |
| 왜 wait 메서드는 반복문 안에서 써야 할까요? (0) | 2020.11.14 |
| race condition : 둘 이상이 같은 자원을 가지고 경쟁한다. (0) | 2020.07.24 |


최근댓글