비교 기반 정렬은, 키 2개를 가지고 비교를 하는 것들을 말합니다. 예를 들어서, 우리가 sort 함수를 호출할 때 이런 식으로 compare 함수를 재작성을 합니다.
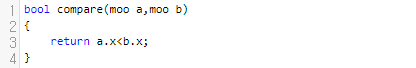
그러면 이것은 key a와, b를 비교한 것입니다. 대다수의 정렬은 이 키 값 2개를 비교해서 순서를 ordering 한다고 보시면 됩니다. 물론 예외가 몇 개 있는데요. 카운트, 버킷, 기수 정렬 등이 예외입니다.
크기가 n인 배열이 있습니다. 물론, 이 n개의 수는 서로 다른 수라고 합시다. 보통 그렇게들 많이 주어지니까요. 그러면, 서로 다른 수 n개를 순서 고려해서 배열하는 가짓수는 n!입니다. 즉, 길이가 n인 순열이 n!개가 나온다는 것입니다.
예를 들어서 n = 4라고 해 봅시다. 그러면 1번째 칸에는 4개 중 하나만 들어가면 됩니다.
그러면, 두 번째 칸에는 2를 제외한 나머지 3개가 들어가면 될 거에요. 이런 식으로 경우의 수를 계산하면 n = 4인 경우 4!이 나옵니다. n = k인 경우 k!이 나올 거고요. 그러면 우리는 a가 b보다 앞선다. 라는 정보를 최소한 몇 개를 가지고 있어야, 어떠한 순열이던지, 유일하게 결정이 될 수 있는지 보아야 할 거 같네요.
잘 보면, 우리는 a가 b보다 크다는 조건이 맞냐? 아니냐만 가지고 후보해를 좁히고 있어요.
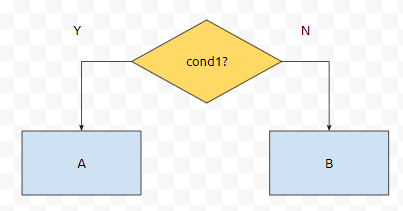
cond1을 수행하고 나서 후보해가 A개, B개가 있어요. 최적의 경우는 cond가 수행되면 거의 절반에 가깝게 나누어 지는 게 좋아요. 왜 그런 특성을 보이는지 귀납법으로 보이도록 합시다. 일단 순열의 갯수가 1개일 때, 비교에 필요한 최소 횟수인, f(1) = 0이에요. 순열이 유일하기 때문입니다.

2개일 때에는 어떤가요? 최소한 1번은 비교해야 합니다. 즉, f(2) = 1입니다. 3개일 때는 어떤가요? 1/2로 나눠지는 경우랑 2/1로 나누어 지는 경우가 있을 거에요. 이 둘은 위상이 같으니까 1/2인 경우만 해 보도록 합시다.
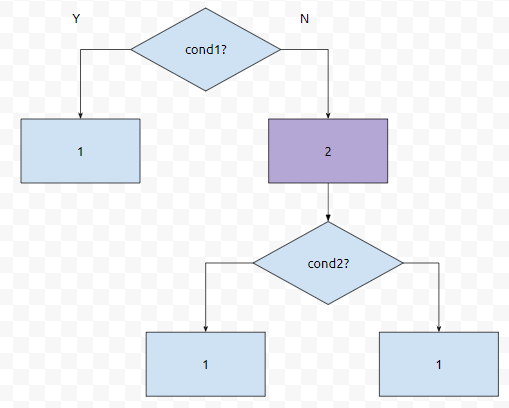
그러면 f(3)은 2입니다. 순열 집합이 3인 경우, 유일한 해를 결정짓기 위해서 최소 2번을 비교해야 하기 때문입니다. 즉, f(2)는 f(1)보다 크거나 같고, f(3)은 f(2)보다 크거나 같습니다. 우리는 0<i<n에 대해서, f(i+1)의 값이 f(i)보다 크거나 같다고 해 봅시다. 그러면, f(n+1)은 f(n)보다 크거나 같을까요?

일단 n+1개의 후보해를 결정 트리로 나눠서 유일하게 해를 결정지어야 하는 경우를 생각해 봅시다. 왼쪽에 1개, 오른쪽에 n개 이런 식으로 나누면 어떤가요? f(1)<=...<=f(n)이라고 했어요. 1로 나눠진 경우는 바로 끝나는데, 그렇지 않은 경우는, 보라색 상태로 가기 때문에 f(n-1)번 만큼 수행해야 합니다.

이 경우는 어떤가요? f(ceil(n/2)) + 1회만 수행하면 됩니다. n>=4라면, ceil(n/2) < n-1이기 때문에, f(ceil(n/2)) <= f(n-1)입니다. 따라서, f(n) = 1 + f(ceil(n/2))가 성립합니다. 최소한 1 + f(ceil(n/2))회 만큼 비교해야 한다는 겁니다. 그러면, f(n+1)의 값은 1+f(ceil((n+1)/2))인가요? a<=b라면 f(a)<=f(b)이므로, 우리는 ceil(n/2) <= ceil((n+1)/2)인지만 보면 됩니다.
먼저, n = 2k (단 k는 자연수) 꼴로 나타내어지는 경우, ceil(2k/2)의 값은 k입니다. 그런데, (2k+1)/2는 k + 0.5이기 때문에, 이것과 가장 가까운 정수는 k+1입니다. 두 번째, n = 2k+1꼴로 나타내어 지는 경우, ceil((2k+1)/2)의 값은 k + 0.5입니다. 이것과 가장 가까운 정수는 k+1입니다. 그런데, (n+1)/2의 값은 (2k+2)/2이니까, k+1입니다. 이것과 가장 가까운 정수는 k+1이기 때문에 ceil(n/2) <= ceil((n+1)/2)입니다.

그러면 대충 이런 식으로 나누는 게 최적이겠군요. 그러면 제가 연두색으로 칠한 것의 크기가 1이 되려면 얼마나 많은 조건을 검사해야 할까요?

대략적으로 log(n)/log(2)회 만큼 검사해야 할 겁니다. 만약에 후보해, 순열의 수가 n!개라면 최소한 log(n!)/log(2)회 검사해야 할 거에요.
log(n^n)은 nlogn입니다. n이 커진다면, n! < n^n인 것은 자명한 사실일 거에요. 일단 n!에 자연 로그인 ln을 씌워 봅시다. 그러면 ln(n!) = ln1 + ln2 + ... + ln(n)이 될 겁니다. 이를 그림으로 나타내 보면 아래와 같습니다.

그러면 ln(1) + ... + ln(n)의 값은 직사각형 넓이의 합입니다. 이 f(x)를 y축 방향으로 -1만큼 평행 이동을 시켜 봅시다.

이 때 우리가 궁금한 것은 x>2일 때, f(x)>g(x+1)이냐는 겁니다. 단 x>2일 때, f(x)>g(x+1)이라면, ln(x) > ln(x+1) - 1이여야 합니다. 이를 잘 정리하면, ln((x+1)/x) < 1인 범위를 구하는 것과 같은데, (x+1)/x < e입니다. 1 + 1/x < e이고요. 그러면, 1/x < e-1이 되는데, x가 양수이므로, 1<x(e-1)이 됩니다. 즉, 1/(e-1)보다 크면, f(x)>g(x+1)이 되는데요. 자연 로그가 대략 2.717xxx 이므로, x>0.58... 어쩌고이면 f(x)>g(x+1)이네요.
그러면 직사각형들의 넓이의 합은, 3부터 n+1까지 g(x)를 적분한 값보다도 크겠네요. f(x) = ln(x)를 부분 적분법으로 적분하면 xln(x) - x가 나옵니다. 그리고 -1을 부분 적분하면 -x가 나오기 때문에, 3부터 n+1까지 g(x)를 부분 적분한 값은 (n+1)ln(n+1) - 2(n+1) - 상수 꼴이 나옵니다.
ln(n!)은 밑이 2인 로그(n!)에 log2/loge를 곱한 거니까, (n+1)ln(n+1) - 2(n+1) - 상수에다가, loge/log2를 곱하면, 배열의 크기가 n일 때, 최적의 방법으로 비교했을 때 비교 횟수가 대략적으로 나오겠군요. 여기서, nln(n)이 2n보다는, n이 커질수록 수가 월등히 커지므로, 상수하고 2(n+1)은 무시합니다. 따라서, 비교 기반 정렬의 복잡도는 하한이 nlogn이 나온다고 보시면 되겠습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 퀵 정렬 : bad partition이 발생할 경우 문제가 된다. (4) | 2019.08.15 |
|---|---|
| 슬립 정렬 : 아이디어는 좋은 거 같은데.. (8) | 2019.08.13 |
| 최대공약수 최소공배수 알고리즘 : 짧은 코드 이해해 봅시다. (2) | 2019.08.07 |
| 약수 구하기 알고리즘 : n^0.5만 보고도 구할 수 있다. (6) | 2019.08.04 |
| 기수 정렬 (radix sort) : 버킷만 있으면 된다. (2) | 2019.08.02 |


최근댓글