ps를 하시다 보면, 이런 말은 한 번쯤 들어보셨을 겁니다. 트리를 일렬로 펴기, 트리를 구간으로 바꿔서 풀기. 자동차 공장 트릭. 이들의 기반이 되는 것은 dfs ordering입니다. 그리고 이를 응용해서, HLD, LCA와 같은 것에도 쓸 수 있습니다. 이 글에서는 HLD, LCA는 다루지 않을 겁니다. 대신에, 트리를 구간으로 바꾸기 위해서 사용하는 전처리에 대해서 알아보도록 하겠습니다.
먼저, 예시로 쓰이는 트리는 아래와 같습니다.

여기서, 이런 쿼리들이 들어온다고 생각해 보겠습니다. 3을 root로 하는 서브 트리에 속한 노드들에 +3을 더한다. 혹은 xor 3을 한다. 이런 것들이 들어올 수 있어요. 트리를 구간으로 어떻게 펴는 것이 가능할까요?

해당 쿼리에서 중요한 것은 부모와 거기에 딸려 있는 자식들입니다. 그러면, 이 자식들은 부모보다 number가 크던지, 아니면 작아야 할 겁니다. 즉, Root, L, R 순으로 탐색을 하거나, 혹은 L, R, Root 순으로 탐색해야 합니다. 보통, 저는 이 둘 중에서 전자의 방법으로 오더링을 합니다.

그렇게 하면, 보라색 부분 정점들의 번호들이, 군청색 부분 번호들보다 작고, 노란색 부분은 보라색, 군청색보다 번호가 작음을 알 수 있습니다. 그러면, 이걸로 어떻게 구간이 만들어 질까요? 해당 방법을 전위 순회라고 하는데요. L[x]는 x를 탐색한 순서가 들어갑니다. R[x]는 어떤 값이 들어가면 좋을까요? x를 루트로 하는 서브 트리에 속한 노드들 중에서 탐색 순서가 가장 큰 값이 들어가면 좋을 겁니다.
탐색 순서는 order 라는 변수가 관여합니다.

1을 기준으로 보면, 자기 자신과 자식들을 다 탐색하고 나서 order의 값이, R[1]의 값이라고 보면 될 겁니다. 이 order의 값은 언제 증가하면 좋을까요? 당연하게도, dfs 과정에서 노드를 새로 방문했을 때입니다.

예를 들어, 7을 방문하고 있는 상태라고 해 보겠습니다. 7은 자식이 없으니, dfs를 수행하지 못하고 빠져 나올 겁니다. 그러면, dfs(5) 함수 내부에 있을 겁니다.
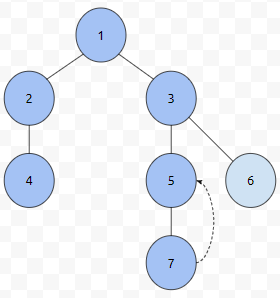
여기서 문제는, 이미 5는 방문했다는 것입니다. 그렇기 때문에 order가 증가하지 않습니다. 그런데 5도 이미 자신의 자식인 7을 탐색했으므로, dfs(5)도 함수 호출을 끝내게 됩니다.

그런데, 이미 3은 방문한 상태인데, 아직 자식들을 모두 방문하지 않은 상태입니다. 즉, 3은 자식들을 탐색하는 과정이였던 셈입니다. 이 때, order의 값은 증가하지 않습니다. 3 입장에서 보면, 3은 visit를 했기 때문입니다.

대신에, 6을 방문할 때 order가 증가합니다. 이 과정을 코드로 옮기면 아래와 같습니다.

dfs는 현재 노드와 parent를 받습니다. root인 경우에, 부모의 값은 -1입니다. 21번째 줄에서만 order가 증가했다는 특징을 잡아낼 수 있습니다.
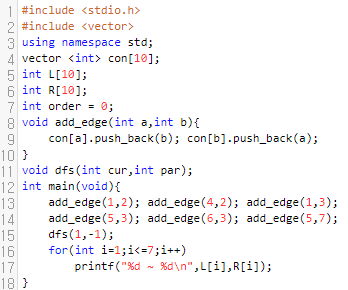
해당 그래프를 생성하고, L과 R의 값을 출력해 보았습니다.
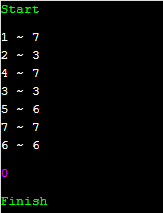
다음과 같이 나옴을 알 수 있습니다. 이것을 씀으로 인해서, 트리에서 탐색 순서가 구간으로 변했다는 것이 핵심입니다. 사람들이 흔히 말하는 트리를 일렬로 펴는 트릭이 이를 의미합니다.
sparse table을 배웠다면, LCA를 구할 때 굳이 이런 전처리가 이용할 필요가 있냐고 생각하실 수도 있습니다. 사실, sparse 테이블 만으로도 해결되기 때문입니다. 그럼에도 불구하고, 의미가 없는 것은 아닙니다. 트리에서 구간을 써야 할 일이 적지 않은 편이기도 하고, LCA를 구하기 위해서는 해당 노드의 부모 노드를 알아야 하는데요.

이 때 부모를 먼저 탐색하고, 자식을 탐색하는 탐색법을 써서, 노드의 부모를 나타내는 pp 배열을 채울 수 있습니다. 생각보다 많이 쓰이는 전처리인 셈입니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 백준 배열 돌리기 5 : 전략적인 브루트 포스로 풀어봅시다. (0) | 2021.04.04 |
|---|---|
| 알고리즘 시간 복잡도 대강 분석하는 방법을 예제를 통해 알아봅시다. (0) | 2021.04.03 |
| 백준 최소 환승 경로 : 허브와 노드를 생각하자. (0) | 2021.02.07 |
| functional graph 에서 사이클을 어떻게 묶어낼까요? (0) | 2021.01.26 |
| 많이 언급되는 오프라인 쿼리 간단하게 훑어봅시다. (0) | 2021.01.04 |


최근댓글