우리가 흔히 말하는 TSP, 외판원 문제는, 어떠한 도시에서 출발해서, 모든 도시를 방문하고 다시 출발점으로 돌아왔을 때, 최단 경로의 길이를 구하는 문제입니다. 이것을 단순하게, 모든 경우를 따져가면서 푼다면 n! 의 가짓수를 모두 따져야 할 겁니다. n이 12만 되어도 4억이 넘어갑니다.
이렇게 비효율적인, 팩토리얼급을 어떻게 지수급으로 낮추느냐가 핵심인데요. 중복된 상태를 memoi 하는 방법으로, O(n^2*2^n)으로 줄일 수 있습니다.
dp를 다음과 같이 정의합시다. 시작점과 끝점은 0이라고 가정합시다.
dp[state][s] : 현재 s에 있고, state 상태일 때 최단 거리.
그러면, 이 state가 무엇인지 궁금하실 텐데요. s에서 출발하였을 때, 방문한 도시들의 집합을 나타낸 겁니다. 방문을 하거나, 안 하거나는 0과 1로 표현할 수 있습니다. 16개의 yes or no. 이는 비트 연산자로 표현할 수 있습니다. 아직, 이 부분에 대해서 익숙하지 않으시다면 다음 두 개의 글을 보고 오셔도 좋겠습니다.
[관련글]
기저 조건을 먼저 생각해 봅시다. n개의 도시를 모두 방문했고, 현재 s라는 위치에 있을 때부터 생각해 봅시다. 이 경우, state는 (1<<n) - 1이 될 겁니다. 당연한 겁니다.
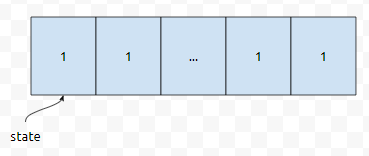
여기에 1을 더하면, 2^n이 되기 때문입니다. 흔히 mask라고 이야기를 합니다. 예를 들어서 255의 경우에, 255에 1을 더하면 256이 됩니다. 255는 이진수로 11111111입니다. 하위 8비트가 모두 1입니다. 65535는 하위 16비트가 모두 1이에요. 65535에 1을 더하면 65536이 되는데, 이는 2^16과 같습니다. 즉, dp[(1<<n)-1][s]는, 도시를 모두 방문한 상태이고, 현재 s 위치에 있다는 건데요. 이때에는 그리 어렵지 않아요. 우리가 0번 도시에서부터 출발해서 0번 도시로 돌아와야 한다고 해 봅시다. 그러면 도시를 모두 방문한 상태에서, s 위치로 왔다면, s에서 0까지 다시 가야 하지 않을까요?
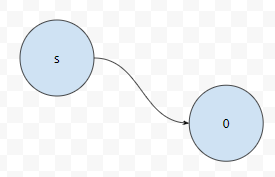
따라서, dp[(1<<n)-1][s]는 dist[s][0]과 같습니다. 이것이 기저 조건입니다. 예를 들어, state가 5이라고 해 봅시다. 그리고, s는 2라고 해 볼까요? 그러면, 상태가 5이고, 현재 2의 위치에 있다는 이야기입니다.
그러면 dp[state][s]는 어떻게 채우면 될까요? 물론 state는 (1<<n) - 1이 아닙니다. state가 5고, 현재 2의 위치에 있다.
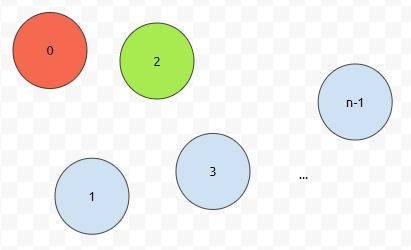
그러면 이런 상태일 거예요. 이 때, 방문을 한 도시는 0과 2입니다. 아직 방문하지 않은 도시는 1, 3, 4, ... , n-1입니다. 이것은 어떻게 판단하면 될까요? 현재 state에서 어떠한 도시가 집합에 속해있지 않은지를 검사하면 됩니다. 그 다음에 어떻게 하면 될까요?
2에서 3을 택했다고 해 봅시다. 그러면 상황이 이렇게 그려질 거에요.

먼저 3을 선택합니다. 그러면 일단 2에서 3으로 가는 비용, 즉 dist[2][3]이 추가될 겁니다.
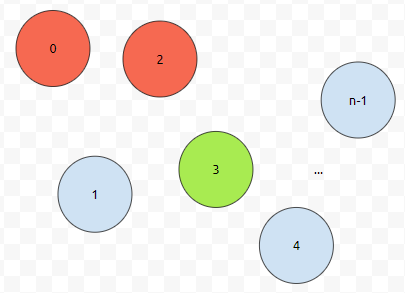
그다음에 어떻게 될까요? 상태는 0, 2, 3번 도시가 켜진 상태인, 8 + 4 + 1 = 13이 될 겁니다. 즉 0.. 01101로 표현이 됩니다. 그리고, 이때, 마지막으로 방문한 위치가 3인가요? 따라서, dp[13][3]의 값을 끌어오면 될 겁니다. 1을 택한 경우에는 어떨까요?

일단 2에서 1로 가야 하기 때문에, dist[2][1]을 끌어와야 할 겁니다.

그다음에 dp[7][1]의 값을 끌어오면 될 겁니다. 이미 방문한 도시는 0, 1, 2이니까 상태 값은 7이고, 마지막으로 방문한 위치가 1이기 때문입니다. 즉, 이미 어떠한 도시가 방문이 되어 있는지를 검사를 하고, 방문을 하지 않았다면, s에서 그 도시까지 가는 비용에다가 dp[state + (1<<to)][to]를 더한 값들이 후보 해가 될 거예요. 그들 중 최소치를 구하면 됩니다. 어렵지 않으니, 이 부분은 코드를 보면서 이야기해 보도록 합시다.

먼저, 우리가 구해야 하는 값은 TSP(1,0)입니다. 이것은 이미 방문한 도시가 0이고, 마지막으로 방문한 도시가 0이라는 의미입니다. 사실 출발지는 반드시 방문했을 수밖에 없습니다.

따라서 상태는 2^0인 1이 되고, 마지막으로 방문한 도시 또한 0입니다. 따라서 TSP(1,0)을 구하면 됩니다.
이제 외판원 순회를 구하는 내부 소스 코드를 봅시다.
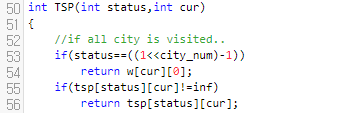
먼저 status가 (1<<city_num) - 1일 때, 즉 모든 도시를 방문했을 때에는, cur에서 0으로 가는 경로의 비용만 리턴합니다. 왜냐하면, 마지막으로 방문한 도시가 cur였고, 결론적으로는 0에 다시 도달해야 하기 때문에 w[cur][0]이 답이 됩니다. 기저 조건에서 이야기를 했었어요.
그리고 55번째 줄에 memoi 한 값이 inf가 아니면 바로 리턴을 시켰는데요. 초기에 tsp[상태][위치]의 값은 inf로 초기화되어있습니다. 어떻게 경로를 돌아도, inf를 초과하지 않는 게 자명하다면, tsp[status][cur]가 inf가 아닌 경우, 이미 이전에 구해놓았다는 겁니다. 따라서, 그냥 그 값을 리턴하면 됩니다.
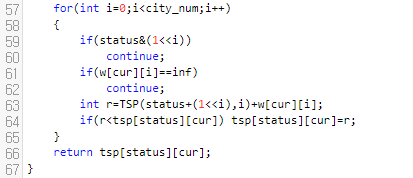
그렇지 않다면, 돌아야 되는데요. status&(1<<i)의 값이 0이 아니라는 이야기는 이미 방문을 했다는 소리입니다. 그렇기 때문에 continue를 시킵니다. 만약에 i를 방문하지 않았다면, status에 i를 더합니다. (status|(1<<i))를 하셔도 됩니다. 사실, (status&(1<<i))의 값이 0이라는 소리는. 결론적으로 말하면 하위 i번째 bit가 0이라는 소리입니다.

그러면 state에 (1<<i)를 더한다면, 하위 i번째 bit가 1이 된 효과가 나타날 겁니다. 그리고, 63번째 줄을 또 보면, w[cur][i]를 더하는데요. 방문하지 않은 도시들 중에서 i를 먼저 방문합니다. 즉 cur에서 i를 방문하기 때문에, w[cur][i]를 더하는 것입니다.
64번째 줄은 후 보해들 중 최솟값을 계속 갱신하는 것이고요.

그런데, 57번째 for문이 도는 횟수가 city_num이 16일 때 3931936번이었습니다. 20일 때에는 1억 번입니다. 이걸 줄이는 방법이 없을까요? 사실, 1/2로 줄어도 빨라질 텐데 말입니다.
팬윅 트리 기법 중에서 1이 켜진, 마지막 bit를 찾기 위해서 쓰는 기법이 하나 있습니다. x&(-x). 여기에서는 아직 안 방문한 마지막 bit를 찾으면 되므로, 일단 state를 뒤집습니다. 이것은 ~state로 할 수 있긴 하지만, 도시가 city_num개가 있기 때문에, (1<<city_num) - 1 - state로 하는 게 조금 더 적절해 보입니다. 예를 들어 도시가 5개라고 해 봅시다.

그러면 이 상태에서 0과 1을 뒤집으면 아래와 같을 겁니다.

이 둘을 더하면 (1<<5) - 1입니다. 즉, (1<<city_num) - 1과 같은 셈입니다.
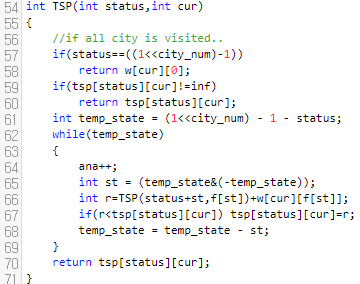
바뀐 TSP 함수입니다. 크게 어려울 건 없고요. f[st]는 다음과 같습니다.
f[st] : 상태 st가 비트 1개만 켜졌을 때, 어떤 비트가 켜졌는가?
예를 들어 f[2]는 1이고, f[4]는 2, f[32]는 5입니다. 이렇게 처리했을 때, 수행 횟수는 n = 16일 때 170만 회, n = 20일 때, 4400만 회 정도였습니다. 이전에 비해 45% 정도만 loop를 돌뿐입니다. 실행 시간은 극적으로 줄지는 않습니다. 백준에서 채점했을 때, 24ms에서 20ms 정도로 줄었습니다. 그렇지만 무의미한 변화는 아닙니다. loop가 45% 정도만 돈 것은, 생각보다 상당히 큰 차이로 나타난 셈입니다.
오늘은 state랑 loc, 이렇게 2차원 dp를 쓰는 외판원 순회 문제를 풀어보았습니다. c언어에서 배운 비트 연산자를 가지고 돌린다는 것이 뭔가 새로웠습니다. 이 기법은 생각보다 ps에서 많이 쓰이기 때문에 익혀두시면 도움이 많이 될 거예요.
'자료알고 > 알고리즘' 카테고리의 다른 글
| stable sort : 우선 순위가 같은 데이터들은 어떻게 정렬될까요? (4) | 2019.07.14 |
|---|---|
| 삽입 정렬 알고리즘 : 원소가 들어갈 위치는 어디인가? (2) | 2019.07.11 |
| 대우 명제 : 언제 이 도구를 증명하기 위해 쓸까요? (0) | 2019.07.06 |
| 냅색 알고리즘 문제 : 가방에 어떻게 넣어야 이득이 최대일까? (0) | 2019.07.03 |
| dfs 심화편 : 깊이 우선 탐색의 단점을 어떻게 보완하는가? (0) | 2019.06.28 |


최근댓글