A(x)을 x의 약수 갯수라고 해 봅시다. 이 때, A(1) + ... + A(n)의 값은 어디에 근접할까요? 이 간단한 질문에서, 오늘의 주제를 이야기 해 보도록 하겠습니다. a가 b의 배수라면, b는 a의 약수입니다. 이 점을 이용해 봅시다.

예를 들어 4의 약수는 1, 2, 4입니다. 그러면, 4는 1의 배수이면서 2의 배수이고, 4의 배수이기도 합니다.
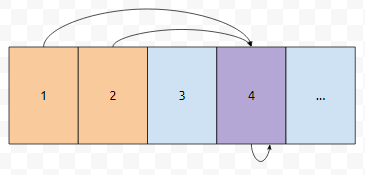
그러면 1에서 출발해서, 1만큼 건너 뛸 때, 2에서부터 출발해서 2만큼 건너 뛰었을 때, 4에서부터 출발해서 4만큼 건너 뛰었을 때, 4를 visit 할 수 있게 됩니다. 그러면 1부터 n까지의 약수의 갯수의 합을 구하는 건 어떻게 하면 좋을까요? 역시 거꾸로 생각하시면 됩니다.

예를 들어서, 약수가 1인 수들을 찾는다고 해 봅시다. 그러면 1, 2, 3, ... , n까지 보면 될 겁니다. n+1은 어떤가요? n보다는 크기 때문에 count를 하지 않아도 됩니다. 약수가 2인 수들은요? [1,n] 범위 내에서요. 마찬가지입니다.
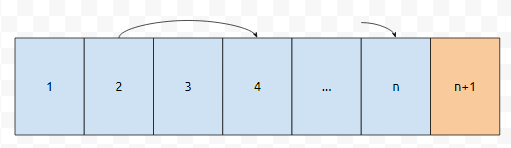
이것도 [1,n]에 속해있는 수들 중, 2의 배수인 것들의 갯수만 찾으면 됩니다. 그러면 대략 [n/2]개인가요? 이는 n/2보다 작거나 같습니다. 이런 식으로 쭉 돌리면, [1,n]에 속하는 자연수들의 약수 갯수의 총 합은 n + [n/2] + ... + [n/n]임을 알 수 있는데요. 이는 n + n/2 + ... + n/n보다 작다고 할 수 있습니다.
위에서 언급한 수식은 n(1/1+1/2+...+1/n)으로 묶을 수 있습니다. 그러면 1/1 + ... + 1/n이 대략적으로 어느 복잡도를 가지는가가 문제가 될 수 있어요. 일단 1/1 + ... + 1/n 은 유명한 조화 급수입니다. ps에서도 간혹 가다 나오는데요. 알아 두시면 좋겠습니다. 이 값을 그림으로 표현해 보면 아래와 같습니다.

이것은 1/x를 1부터 n+1까지 적분한 값 보다는 큽니다. 이 값은 ln(n+1)이 됩니다.

이 값은 보라색 + 초록색으로 칠한 부분의 합으로도 표현이 될 수 있는데요. 보라색의 넓이는 1입니다. f(1)의 값이 1이기 때문입니다. total 넓이에서 보라색 부분만 빼 봅시다.

이제 초록색 사각형들을 x축 방향으로 1칸씩 왼쪽으로 이동해 보겠습니다.

이 값은 1/x를 1부터 n까지 정적분한 값보다는 작습니다. 즉, 문제의 값 T는 ln(n+1)보다는 크고, T-1은 ln(n)보다는 작다는 소리가 됩니다. 즉, ln(n+1) < T < ln(n) + 1이 성립하겠군요. 이 n의 값은 1 + 1/2 + ... + 1/n인데요. 제가 구하려고 하는 문제의 값은 n + [n/2] + ... + [n/n]이였습니다. 이 값은 n + n/2 + ... + n/n보다 작거나 같기 때문에, nln(n) + 1보다 작거나 같을 겁니다. 즉, (1+1/2+...+1/n)은 대략, ln(n)으로 봐도 됩니다.
따라서, 구간 [1,n]에 속하는 자연수들의 약수의 갯수의 합은 대략 nln(n)에 근사하다고 보셔도 좋습니다.
그러면, AB = C이면서 abs(A-a) + abs(B-b) + abs(C-c)의 값을 최소화 하는, 백준 14279번 문제는 어떻게 풀면 좋을까요? A, B, C는 양의 정수여야 합니다. 단, a, b, c의 값은 1보다 크고 100만보다 작거나 같은 자연수입니다. 이것을 그냥 보면 굉장히 어려워 보입니다.
일단 abs(A-a) + abs(B-b) + abs(C-c)의 값이 300만보다 작거나 같은 경우가 있다는 것을 보여 봅시다. A = 1이고, B = 1이면 C = 1입니다. 이 때, abs(1-a) + abs(1-b) + abs(1-c)의 값을 구해야 하는데요. f(x) = abs(1-x)라고 하면 f(x)는 다음과 같이 그릴 수 있습니다.

그러면, f(x)의 값은 [0, 100만] 범위에서는 f(100만)일 때가 가장 클 겁니다. 이 때 f(x)의 값은 100만보다 작습니다. 따라서, abs(A-a) + abs(B-b) + abs(C-c)의 값이 300만보다 작거나 같은 경우가 존재합니다. 그렇다면, A, B, C는 어느 범위까지 보면 좋을까요? A>a이고 B>b이고 C>c라고 합시다. 그러면 A-a가 300만 이하일 때 까지 보면 될 겁니다. B-b도 마찬가지이고요. C-c도 마찬가지입니다. 이 셋을 동시에 만족하려면, A<a+300만, B<b+300만, C<c+300만이 됩니다. a와 b와 c의 최댓값은 100만이기 때문에, A도 400만 이하, B도 400만 이하, C도 400만 이하일 때 까지 보면 됩니다.

저는 그냥 적당하게 600만까지 보게끔 선언을 해 놓았습니다. 그런데 AB = C를 만족해야 합니다. 그러면 어떻게 처리해야 할까요? 간단합니다. A는 1부터 sz까지 탐색합니다.

이 때 B는 A*B의 값이 sz보다 작거나 같을 때 까지만 탐색하면 됩니다. 즉, 구간 [1,sz]에 속하는 자연수들의 약수 갯수의 총 합만큼 loop가 돕니다. 시간 복잡도는 szln(sz)가 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 팬 케이크 정렬 : 위에서부터 k개를 뒤집는다. (10) | 2019.09.17 |
|---|---|
| 라빈 카프 알고리즘 : 그래도 비벼볼 만한 문제가 있다. (6) | 2019.09.06 |
| 에라토스테네스의 체 : 소수가 아닌 것들을 지운다. (7) | 2019.09.02 |
| 중복 조합 : 어떻게 ps에서 쓰일까요? (3) | 2019.08.24 |
| 왜 유클리드 알고리즘 함수는 최악의 경우 O(log)일까? (2) | 2019.08.21 |


최근댓글