Quick sort, selection을 할 때 pivot을 선택하는 전략을 찾아보면 꽤 많이 나온다는 것을 알 수 있습니다. 이번 시간에는 median of median을 해 보도록 하겠습니다. 중간값의 중간값? sort 구현체를 찾아보면 Median of Median으로 하는 거 같지 않은데, 이건 또 왜 그럴까요?
중앙값부터 보겠습니다.
[5, 3, 6, 4, 7]의 중앙값은 무엇인가요? 5입니다. 왜냐하면, 이것을 sort를 하면 [3, 4, 5, 6, 7]입니다. 5가 딱 중간에 있기 때문입니다. 크기가 n인 배열을 생각해 보겠습니다.

이것을 우리는 5등분을 하겠습니다. 예를 들어, 배열이 [2, 5, 3, 2, 7, 2, 7, 3, 6, 4, 7, 5, 7, 2, 3, 6, 6, 4, 35, 37, 7, 33, 45, 36, 1] 이렇게 있다고 해 보겠습니다.

그러면 이것을 [2, 5, 3, 2, 7], [2, 7, 3, 6, 4], [7, 5, 7, 2, 3], [6, 6, 4, 35, 37], [7, 33, 45, 36, 1] 이런 식으로 나눌 수 있습니다.

구간의 길이가 15 이하일 때에는, 삽입 정렬을 이용해서 median 값을 구하면 됩니다. 그렇지 않으면, 어떻게 하면 좋을까요? 먼저, 각 구간별로 중앙값을 구합니다. 이것은 보라색으로 표시해 놓았습니다.
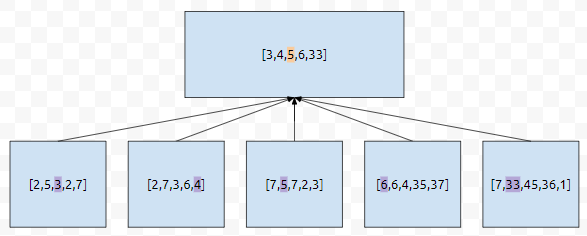
그러면, 작은 문제들의 대표값은 3, 4, 5, 6, 33이 됩니다. 이것을 큰 문제에 반영합니다. 즉, 길이가 25인 배열에서의 문제에서, 힌트 5개인 3, 4, 5, 6, 33을 얻어냈습니다. 여기서 하나 문제를 드리겠습니다. 큰 문제에서, 5라는 값을 중앙값으로 취하면 어떨까요? 즉, 구간 A가 a, b, c, d, e로 나누어 졌다고 합시다. a, b, c, d, e에서 구한 값들의 중앙값을 A에 반영하면 어떨까요? 이것을 슈도 코드로 표현하면 아래와 같습니다.

그리고 길이가 n인 배열에 대해서 위 함수를 재귀적으로 호출해서 나온 결과를 pivot으로 취하려고 합니다. 현명한 방법일까요?
인위적으로 데이터를 만들어 보면 그렇게 하면 안 된다는 것을 알 수 있습니다. 작은 구간 5개 중에서, 3개는 정렬했을 때, 같다고 해 보겠습니다. 나머지 2개는 3개의 구간 안에 있는 제일 큰 수보다 크다고 해 보겠습니다. 그러면, 작은 구간 5개가 합쳐진 큰 구간 하나는 아래와 같이 그려질 겁니다.
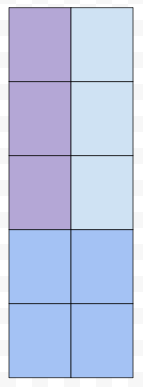
군청색 부분은, 보라색과 하늘색보다 큽니다. 제가 그린 구간들의 M of M은 보라색들보다는 확실히 크거나 같지만, 하늘색과 군청색보다는 최악의 경우, 작습니다. 제가 그린 구간 내에서 M of M 값은 보라색 안에 있을 겁니다. 보라색은 전체의 3/10을 차지합니다.

똑같은 방법으로 확장해 보겠습니다. 작은 구간의 미디안 값은 보라색, 보라색, 보라색, 노란색, 노란색입니다. 위에서, 보라색 < 하늘색 < 군청색이라고 했습니다. 그리고 군청색 < 노란색이라고 해 봅시다. 제가 구한 방법에서 Median 값은 전체의 9/25보다는 크거나 같지만, 나머지 16/25보다는 작습니다. 9/25를 주목해 봅시다.
9/25는 3/10에다가 3/5를 곱해야 나옵니다. 당연하게도, 구간이 5^k배가 커지면, 제가 뽑은 pivot보다 작거나 같은 수의 갯수는 3^k배 만큼 커질 겁니다. 퍼센테이지로 따지면 (3/5)^k만큼이 곱해지는 것인데요. k가 무한대로 가면, 당연하게도 이 값은 0에 가까워 집니다. 사실 k가 10만 되어도, 0.006이 곱해집니다. 0.006은 0.6%와 같습니다. 10000개의 데이터가 있다면 60개만 피벗 왼쪽에 있고, 나머지 9940개는 피벗 오른쪽에 있다. 별로 좋지 않은 상황입니다. skew가 된 셈이죠. 그러면, 이 아이디어는 쓸모가 없는 것일까요?

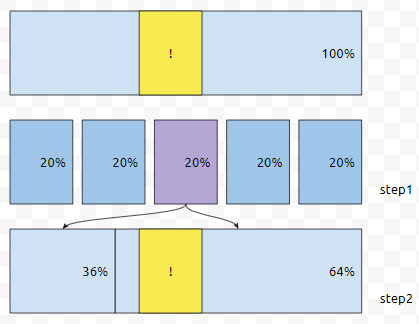
11이라는 값을 우리는 Median of Median으로 재귀적으로 리턴하는 것은, 제가 테스트 케이스를 들어서 안 된다고 하였습니다. 관점을 바꿔 봅시다. 25개짜리 배열의 Median of Median을 구할 때, 11을 피벗으로 삼으면 어떨까요? 그러면 최소한 1, 2, 3, 6, 7, 8, 9, 10, 11 이렇게 9개는 25개짜리 배열의 M of M을 구하기 위해서 설정한 피벗 11보다 작거나 같음을 알 수 있습니다. 이 비율은 9/25. 36%입니다. 이것을 잘 써먹는 방법은 11을 그대로 리턴하는 게 아니라, 11을 피벗으로 이용해서, 큰 문제에서의 중간값을 찾는 것입니다.
문제를 이렇게 바꾸어 보겠습니다. 크기 n짜리 배열에서, n/2번째로 큰 수를 찾아라. 그리고 작은 문제들도, 작은 배열에서의 median을 찾아라.

문제의 !을 찾을 때, 최악의 경우라도 0.64배율씩 줄고 있음을 알 수 있습니다. 이분 탐색이 반씩 줄여나간다면, 이것은 최악의 경우라도 0.64배씩 줄여나가는 셈입니다. (0.99)^x와, (0.64)^x는 0에 가까워지는 속도 자체가 다른데요. 아래 그래프를 보아도 알 수 있습니다.

이는, 효율성과도 연결되는 부분입니다.

이를 간단하게 슈도 코드로 나타내면 위와 같습니다. 당연하게도, findkth는 pivot 값인 tempM[2]을 가지고 구간을 좁혀 나갈 겁니다. pivot을 기준으로 왼쪽에 있다 싶으면 왼쪽 array만 취하고, 우측에 있다 싶으면 우측 array만 취하는 것은 Quick selection이나, quick sort를 구현해 보셨다면 대략적으로 이해하실 거라 생각합니다.
이제, 시간 복잡도를 구하기 위한 관계식을 만들어 보겠습니다. 길이가 n인 배열에서 Median of median을 구하기 위해서는, 작은 덩어리 5개로 쪼개서, 같은 일을 해야 합니다. 이것은 5T(n/5)로 표현할 수 있습니다. 다음에 피벗에 따라서 36%짜리로 가느냐, 64%짜리로 가느냐가 나누어 지는데요. 계속 64%에만 걸렸다고 가정하겠습니다.
즉, T(n) = 5T(n/5) + T(0.64n)입니다. 게다가 우리는, 5개의 길이가 똑같은 배열로 나누었으니, 이에 대한 복잡도 n도 추가해야 겠네요. 즉 T(n) = 5T(n/5) + T(0.64n) + n입니다. 이걸 마스터 정리로 계산을 할 수 있지만, 우리는 코드를 작성할 수 있으니, 간단하게 코드를 작성해서 돌려보도록 하겠습니다.

10배가 늘어날 때 마다 몇 배로 뻥튀기가 되는지 보겠습니다.
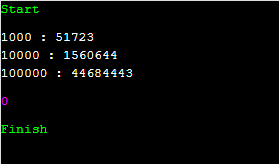
n의 크기가 10배 늘어날 때 마다 T(n)값은 30배씩 뻥튀기가 된다는 것을 볼 수 있습니다. 즉, 10^a = 30에서 a는 log(30)입니다. 뭔가 익숙한 거 같은 log(3). log(30)은 1+log(3)과 같습니다. 이걸 상용로그표를 보고 계산하면 1.4771입니다. 복잡도가 O(n^1.4771)인 셈입니다. 앞에 붙는 상수는 1.83. 쓸 만하지 않아 보이는군요.
그러면 이 아이디어가 쓸모가 없는 걸까요?
후보해를 1/5로 나눠서 5번 수행하기 보다는, 5개씩 나눠서 그것들의 중앙값들만 다시 새로운 배열에 넣고, 거기서 또 중앙값을 뽑으면 어떨까요?
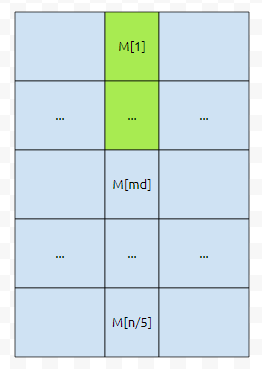
n이 매우 크다면, 중앙에 있는 M[1], ... , M[n/5] 중에 초록색으로 칠한 부분은 전체 대비 1/2에 가까울 겁니다. 여기서 원소가 1개가 추가된다고 그 비율이 크게 바뀌지는 않습니다. 즉 초록색 부분은 전체의 1/2에 가깝다고 해석해도 됩니다.
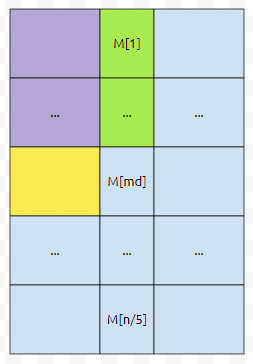
보라색 + 초록색 + 하늘색 열에서, 보라색 + 초록색이 차지하는 비중은 3/5입니다. 노란색 + 하늘색으로 이루어진 하나의 열에서는 노란색이 차지하는 비율은 2/5입니다만, 보라색 + 초록색이 압도적으로 많습니다. 5개씩 쪼갠 작은 배열을 M이라 합시다. M의 중앙값은, 전체의 3/10보다는 최소한 클 겁니다.

즉, 우리는 1/5씩 줄여가면서 피벗값을 찾고, 그것을 토대로 k번째 값을 찾아나가는 겁니다. 이 때, T(n)의 관계식은 최악의 경우에, T(n) = T(n/5) + T(0.7n) + 3n이 됩니다. 이 관계식을 풀어 보겠습니다.

이렇게 들어갔을 때, n이 1만, 10만, 100만일 때 차례대로 봅시다. n^1.477일 때와 비교하면 효율적임을 알 수 있어요. 다만, 상수가 생각보다 크다는 것은 무시하지 못합니다. 앞에 상수가 21, 24, 26. 여기에 피벗을 뽑고 난 다음에 부분 문제에 들어가는 것도 고려를 한다면, 꽤 무겁다고 할 수 있습니다. 이건 최악이라서 그럴 수도 있을 듯 싶습니다. T(n) 관계식에서 3n 자체도 무시할 만한 factor는 아닙니다. median들의 median을 pivot으로 뽑았을 때, 이것이 정확하게 딱 중간값인 경우가 최적일 건데, 그 경우에도 3n이 붙으면 가볍지는 않습니다.
T(n) = 2T(n/2) + 3n 이 전략을 그대로 Quick sort의 피벗 전략으로 넣었을 때 Quick sort의 수행 시간을 구하기 위한 재귀 관계식입니다. 여담이지만, 링크에 따르면 이것의 상수값을 2.95로 줄일 수 있다고 합니다. 24n, 9.9n과 2.95n은 상당한 차이가 있습니다. 상당히 매력적인 듯 싶습니다. 그런데, 사실 2.95n짜리 피벗 전략을 구현하느니, merge나 heap을 쓸 듯 싶습니다. 그럼에도 불구하고 한 번 정도는 배워보고, 구현해 볼 만한 가치는 있습니다. 왜 이 방법이 안 되는지, 왜 이렇게 해야 하는지, 분할 정복은 어떨 때 쓰면 안 되는 건지, 어떨 때 써야 하는지 삽질하면서 배워가기에는 좋기 때문입니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 슬라이딩 윈도우 알고리즘 : 2개의 커서가 중요하다. (2) | 2020.07.29 |
|---|---|
| amortized 복잡도 : average complexity와 뭐가 다른가요? (2) | 2020.07.16 |
| lis 알고리즘 : lower_bound 이용해서 그리디하게 해결해 봅시다. (0) | 2020.06.17 |
| 카카오 호텔 방 배정 : map 을 이용해서 깔끔하게 처리합시다. (0) | 2020.05.09 |
| event driven : ps 문제에서 간단하게 활용해 봅시다. (0) | 2020.05.01 |


최근댓글