안녕하세요. 백준에서 chogahui05로 활동하고 있는 조경완입니다. 트라이에서 x진법으로 쪼갠다. 무슨 소리일까요? 사실 Trie가 어떤 것을 처리하기 위한 자료구조인지는, 카카오 문제에 출제되어서 익숙하신 분들이 많으실 거라고 생각합니다. 여기서 한 단계 더 깊이 들어가 보도록 하겠습니다.
공간을 줄이기 위해서는 어떻게 잘 쪼개야 할까요?
먼저 소문자로만 이루어진 문자열들을 Trie에 넣었을 때 상황을 생각해 보겠습니다. 문자열들의 길이 합은 10만을 넘지 않는다고 해 보겠습니다. 그리고 소문자만 나온다고 해 보겠습니다.

그러면, 다음과 같이 정적 Trie를 구축할 수 있을 겁니다. 여기서 26은 다음을 의미합니다.
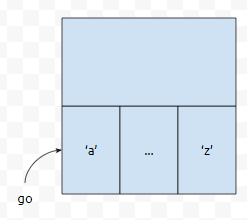
'a'가 나왔을 때, 'b'가 나왔을 때, ... , 'z'가 나왔을 때 어디로 갈 건지. 어디로 갈 것인가라는 정보를 각 노드마다 26개씩 저장하고 있어야 하기 때문에, 26이 나온 것입니다. 'a', ... , 'z'는 각각 0, ... , 25로 표현할 수 있습니다. 이 중 최댓값인 25를 3진법으로 쪼개 보겠습니다. 25을 3진법으로 표현하면 아래와 같습니다.

만약에 'z'라는 문자열이 들어왔다면, 트라이에 어떻게 들어가는지 보도록 하겠습니다. 3진법은 자릿수가 [0, 2] 범위에 있습니다. 그러므로, 작은 노드당 3개의 포인터를 가질 겁니다. 'z'는 3진법으로 221로 표현됩니다. 이것을 Trie에 추가해 보도록 하겠습니다.

먼저 2가 들어왔습니다. root의 go[2]와 node1을 연결합니다. root에서 2로 들어갔을 때 node1이 나온다는 의미입니다.

다음에 node1의 go[2]와 node2를 연결합니다. 이는, root에서 출발했을 때, 22를 거치면 node2에 도달한다는 의미입니다.
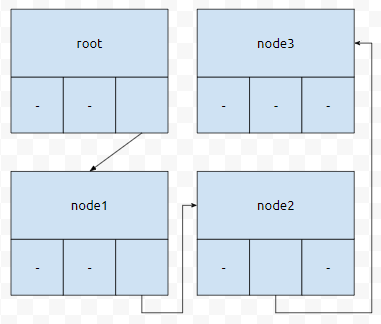
다음에 node2의 go[1]과 node3을 연결합니다. 이는 root에서부터 출발했을 때 221을 거치면 node3에 도달한다는 의미입니다. 그러면, 'z'를 추가했을 때, 추가된 go 포인터는 몇 개일까요?

9는 26보다 작습니다. 따라서, 26개의 pointer를 깡으로 밀어 넣는 것보다, 3진법으로 쪼개서, 작은 노드당 3개의 pointer를 밀어넣는 것이 공간적으로 효율적입니다.
그러면 나올 수 있는 문자 종류가 26개일 때, 3진법으로 쪼개는 것이 이득일까요? 쪼갠 노드당 pointer 갯수는 k개로 쉽게 구할 수 있습니다. k진법으로 쪼갰을 때, 최대 자릿수는 ceil(log(26)/log(k))로 구할 수 있습니다.

위 프로그램은, 26을 zi진법으로 표현했을 때, 몇개의 자릿수로 표현되어야 하는지 계산하는 함수입니다. 예를 들어서, zi가 2라면, 5입니다. 2진법으로 11111이 10진법으로 31이기 때문입니다.

계산 결과를 보면 zi가 3일때, 최대 자릿수와 작은 노드당 포인터의 갯수의 곱이 제일 작다는 것을 알 수 있습니다. 따라서 우리는, 총 n개의 문자가 들어오면, 정적 Trie를 다음과 같이 구성할 수 있습니다.

이 때, Trie에서 pat을 찾을 때 시간 복잡도는 어떻게 될까요? 1개의 문자가 3개의 문자라고 해야하는지 상태라고 해야하는지로 쪼개졌습니다. 따라서, O(3|pat|)이 되고, 시간 복잡도는 상수를 무시하므로, O(|pat|)이 됩니다. 여기서 중요한 것은 [n][26]을 [3*n][3]으로 공간을 줄였다는 것입니다.
이제 다른 문제를 생각해 보겠습니다. 수가 들어오고 제거가 될 때, k번째로 작은 수를 구해야 하는 Query를 생각하겠습니다. 적당히 들어오는 수의 범위를 [0, 2^30-1] 이라고 해 봅시다. 이것은 어느 진법으로 처리하면 좋을까요?

10번째 줄만 바꿔 보겠습니다. cur >= (1LL<<30)으로 말입니다. 그러면, 한 개의 수가 들어왔을 때, 노드 당 포인터가 몇 개가 필요한지와, 노드가 몇 개가 필요한지가 나올 겁니다.

10억은 상당히 큰 수입니다. 그러므로, 수 x가 k진법으로 어떻게 나오는지 미리 전처리 할 수가 없습니다. 이 점을 감안해 봅시다. 어떠한 수 x를 k진법으로 변환하려면 나누기 연산과 모듈러 연산을 해야 합니다. 이 둘은 생각보다 무거운 연산입니다. 이 둘을 피하려면, 2, 4, 8 등의 2의 거듭제곱 꼴로 나누어야 합니다.
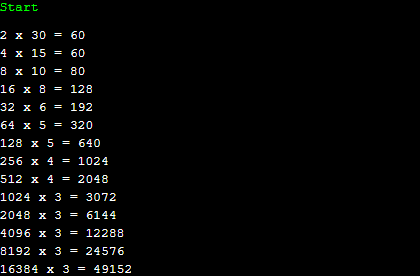
후보해들을 보니, 수 하나를 추가할 때 마다 최악의 경우, 2진법 기반으로 추가하면 60개, 4진법 기반은 60개, 8진법 기반은 80개, ... 의 포인터를 추가로 소모합니다. 수가 20만개 정도가 들어오면 대충 16진법까지 커버가 될 수 있습니다. 128메가 기준으로요. 코딩하기 편한 쪽은 2진법이지만 뎁스는 4, 8, 16으로 갈수록 극단적으로 낮아지는 것을 볼 수 있습니다.

Trie는 크게 보면 List 구조입니다. 포인터를 통해서 A노드에서 B노드로 이동했다고 해 봅시다. A와 B는 연속적인가요? 그럴 수도, 아닐 수도 있습니다. 멀리 멀리 뛴다면, 그만큼의 오버헤드가 걸릴 수 있습니다. 따라서, 이 수치를 낮추는 것이 중요합니다. 그런데, 탐색 횟수 10과 8은 그리 크지 않은 차이입니다. 그러면, 공간도 적절히 쓰고, 탐색 깊이도 적절히 작은 8진법 기반으로 탐색하는 것을 생각해 볼 만 합니다.

어떠한 수를 8진법으로 뽑아보겠습니다. mask 값을 7로 두고, 오른쪽 shift 연산을 써 봅시다.
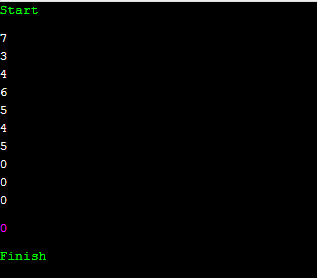
그러면 정확하게 8진법으로 뽑아낼 수 있습니다. 10억을 Trie에 넣을 때에는 7, 3, 4, 6, 5, 4, 5, 0, 0, 0 순으로 search 하면서 넣으면 됩니다. 저는 이 포스팅에서 Trie를 이용한 기법으로 kth를 구할 때 2진법을 이용해서 넣는 것을 소개했는데요. 그 이유는 코딩이 정말 간단하기 때문입니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| java에서 STL의 multimap 구조를 구현해 봅시다. (2) | 2020.06.24 |
|---|---|
| marking 배열과 sparse array (0) | 2020.06.19 |
| 랜덤 접근이 가능한 deque 자료구조를 chunk로 구현하면 어떤 이점이 있을까요? (6) | 2020.04.07 |
| 세그먼트 트리 구조에서 lazy propagation을 적용하는 코드를 뜯어봅시다. (0) | 2020.03.31 |
| 유니온 파인드 (union find) : 병합 연산과 루트를 찾는 연산만 있다. (2) | 2020.03.14 |


최근댓글