세그먼트 트리를 모를 때, k번째로 빠른 수를 어떻게 찾아야 할 지 모를 때, 어떤 방법을 쓰면 좋을까요? n이 적당히 크다면, 우리는 이런 아이디어를 생각해 볼 수 있습니다. 구간이 n개가 아닌 sqrt(n)개. 그리고, 구간 별 원소 갯수도 sqrt(n)개. 사실, 이것을 응용한 알고리즘이 Mo's algorithm인데, 여기까지 다루지는 않겠습니다.
예를 들어, 배열의 임의의 원소가 구간 [1,9]에 속하는 자연수라고 해 봅시다. 이 때 배열 [1, 3, 3, 4, 4, 5, 5, 6, 7, 7, 7, 8, 8, 9]에서, 13번째로 작은 수를 찾기 위해서 어떻게 하면 좋을까요? 일단, co[x]는 x가 나타나는 빈도수를 나타낸 겁니다.
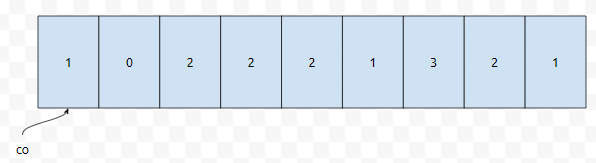
그러면 단순하게 생각하면, 누적 값을 더해가면서, 1이 출현하는 빈도수부터, i가 출현하는 빈도수까지의 합을 계산했을 때, 13보다 크거나 같아지는 최초의 i를 찾으면 될 겁니다.

예를 들자면, 이 경우, 8이 답이 됩니다. 이는 co[1] + ... + co[8]의 값이 13이기 때문입니다. 그러면 1부터 9까지 모두 돌면서 확인을 하는 수 밖에 없을 거에요. 만약에 배열에 들어올 수 있는 수가 구간 [1,10만]의 범위에 있다면 어떨까요? 이 때에는, k번째로 작은 수를 구하기 위해서 n번을 탐색해야 할까요?
사실, 업데이트가 없다면, 그냥 누적합을 미리 구해놓고 있으면 됩니다. 그런데, 업데이트가 일어난다면 이야기가 달라집니다. 여기서 좋은 아이디어가 없을까요?

우리는 sqrt(9) = 3개의 큰 덩어리로 나눌 수 있어요. 이들은 9/3 = 3개씩 원소를 가질 수 있어요. 이걸 그림으로 나타내면 위와 같은데요. 큰 덩어리 1번은 1, 2, 3을, 큰 덩어리 2번은 4, 5, 6을, 3번은 7, 8, 9를 cover 합니다. 이런식으로 하면, k번째 수를 어떻게 찾으면 될까요? k = 13이라고 해 봅시다. 그러면 큰 덩어리들을 먼저 봅시다.
3+5는 8인데, 이 값은 13보다는 작습니다. 3+5+6 = 14인데, 이것은 13보다 크거나 같은 최초의 위치입니다. 따라서, 3번째 덩어리에서 찾을 건데요. 이들은 7번, 8번, 9번을 cover 합니다. 누적 count는 8부터 시작할 겁니다.

그 다음에 어떻게 할까요? 큰 덩어리 위치는 알았으니까 7번부터 탐색을 합니다. 8+3은 13보다는 작아요. 하지만, 8+3+2는 13보다 크거나 같습니다. 즉 주황색으로 칠한 위치에서 13보다 크거나 같은데요. 8번째 위치에서 13보다 크거나 같았음을 알 수 있습니다.
따라서 8을 리턴하면 됩니다. 여기서 뭔가 다른점을 눈치 채셨을 건데요. 그냥 1개씩만 보았던 것을, 필요한 경우에, 크게 크게 보았다는 것이 다른 점입니다. 3개씩 막 건너뛰고 있어요. 큰 덩어리도 많아봤자 sqrt(n)개, 덩어리 하나 당 많이 가져봤자 대략 sqrt(n)개이므로, k번째 수를 구하는 연산은 최악의 경우 O(root(n))에 동작합니다. 이 점은 굉장히 중요한 점입니다.
그러면, 어떠한 수가 배열에 add가 되고, delete가 되었을 때 처리는 어떻게 해야 할까요? 간단합니다.
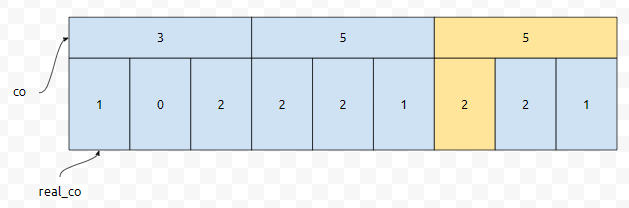
7이 제거되었다고 해 봅시다. 그러면, real_co[7]의 값을 하나 감소시킵니다. 그런데, 여기서 중요한 것은 몇 번째 덩어리도 감소해야 하나요? 3번째 덩어리도 감소해야 하나요? 왜냐하면 3번째 덩어리에 포함된 7의 갯수가 하나 감소했기 때문입니다. 따라서, 3번째 덩어리의 대표값은 6에서 5로 줄어듭니다.

다음에, 3이 추가되었다고 해 봅시다. 그러면 real_co[3]의 값이 하나 증가하면 될 거에요. 그런데, 이 때, 3이 몇 번째 덩어리에 속해있나요? 1번째 덩어리에 속해 있어요. 따라서, 1번째 뭉치의 대표값이 3에서 4로 증가해야 합니다. 이걸 저는 2차 구조라고 이야기를 하겠습니다. 사실, 3차, 4차 구조도 비슷하게 응용하면 만들 수 있습니다. 예를 들어 3차 구조는 아래와 같을 겁니다.

그러면 이 경우, k번째 원소를 구하는 연산의 복잡도는 O(n^(1/3))이 될 겁니다. n이 100만일 때 단 300번 가량의 연산만을 수행하면 된다는 것입니다. 4차 구조인 경우에는 121번 정도면 끝납니다. 재귀 호출로 구현한 세그 트리가, 상당히 느릴 수도 있다는 것을 생각하면 어마어마하다는 것을 알 수 있습니다. 코드가 다소 복잡해 지는 건 기분 탓이겠지만요.
그러면 간단하게 코드만 봅시다.
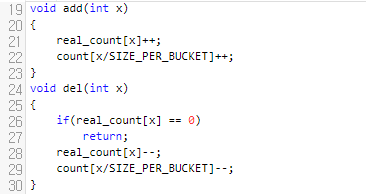
SIZE_PER_BUCKET은 덩어리 하나당 몇 개의 원소를 가지고 있는지를 나타냅니다. 배열의 size가 10만인 경우, 이 값을 보통, 320 정도로 잡습니다. 50000이면 225, 20만이면 450. add와 del 함수 정도는 쉽게 이해하실 수 있을 겁니다. 여기서 count[x]는 덩어리 x에 대해서 몇 개의 원소들이 있는지를 나타낸 것입니다. 그리고 real_count는[x] 실제로, x가 몇 개 있는지를 나타냅니다.
x번은, x/320번 덩어리에 있습니다. 따라서, x가 추가되면, x/320번 덩어리의 count 값도 같이 증가해야 합니다. x가 삭제된다면 반대로, x/320번 뭉치의 값도 하나 줄어들어야 할 거에요.

kth 함수가 조금 길어보이니, 자르겠습니다. 먼저, 43번째 줄까지는 배열을 오름차순으로 정렬했을 때, t번째 수가 있는 덩어리 번호를 구합니다. 만약에 그 번호를 구하지 못하면 lo 값이 -1일 텐데요. 이 경우, 배열에 있는 수의 갯수보다 t가 더 큰 것이므로, -1을 리턴합니다.

덩어리 번호를 구했다면, 그 이후부터는 어렵지 않습니다. 이미, 뭉치들의 대표 값들의 합은 43번째 줄을 수행할 때, nj_t가 가지고 있습니다. 그러면 우리는 덩어리 안에 있는 수들이 몇 번 나왔는지에 대한 값을 nj_t에 계속 넣어가면서 계산해 주면 될 거에요. 최종적인 시간 복잡도는 O(root(n))입니다.
이를, sqrt decompositon, 평방 분할이라고 이야기를 합니다. 의외로 알아두면 좋은 아이디어이니, 알아두면 좋을 듯 싶네요.
'자료알고 > 자료구조' 카테고리의 다른 글
| 희소 행렬 (sparse matrix) : 어떤 정보가 중요한가? (6) | 2019.09.27 |
|---|---|
| LRU 알고리즘 : 리스트를 활용해서 구현해 봅시다. (6) | 2019.09.23 |
| 재해싱 (rehashing) : 시간 복잡도를 분석해 보면서 왜 필요한지 알아봅시다. (4) | 2019.09.13 |
| 자료구조 해시 테이블 : 직접 구현해 봅시다. (8) | 2019.09.11 |
| 자료구조 덱 (deque) : 앞과 뒤에서 추가되고 삭제된다. (2) | 2019.08.22 |


최근댓글