오늘도 어김없이 신기한 정렬을 들고 왔습니다. 바로 바이토닉 정렬입니다. bitonic sort라고도 하는데요. 증가했다, 감소하거나, 감소하거나 증가하는 수열을 우리는 바이토닉 수열이라고 합니다. 말로 설명하면 쉽지 않으니, 간단하게 n = 8 데이터를 가지고 sort를 해 봅시다.
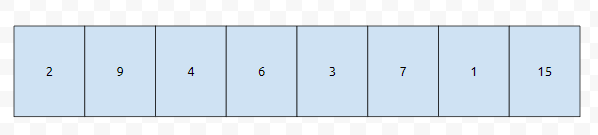
먼저 다음과 같은 배열이 있다고 가정해 봅시다. 이것을 우리는 오름차순으로 정렬해야 합니다. 어떻게 하면 좋을까요?

일단, 초록색, 보라색, 노란색, 하늘색 순서대로 칠해 봅시다. 이들은 1칸 차이이기 때문에 서로 인접해 있습니다. 이제 우리는 어떻게 할 것이냐면, 초록색은 증가, 보라색은 감소, 노란색은 증가, 하늘색은 감소가 되게 할 거에요.
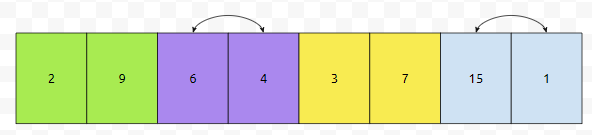
그러면 이렇게 될 겁니다. 1회전이 끝났습니다. 이제 2회전을 돌려 봅시다.

초록, 보라, 노랑, 하늘색 순서대로 봅시다. 이걸 자세히 보면, 4개 단위를 기준으로 서로 엇갈려서 놓여진 것을 볼 수 있어요. 연두, 보라, 연두, 보라가 놓여 있고, 다음에 노랑 하늘 노랑 하늘 이렇게 놓여 있어요. 초록색이랑 보라색은 증가, 노랑색과 하늘색은 감소해야 합니다.
만약에 이 조건에 맞지 않으면, 같은 색으로 칠한 두 부분은 서로 바꾸어야 합니다.

그러면 바꿔야 할 것은 9와 4, 그리고 3과 15임을 알 수 있어요. 보라색은 증가해야 하고, 노란색은 감소해야 하는데, 9 - 4는 감소하고, 3 - 15는 증가해야 하는데 감소하기 때문입니다.
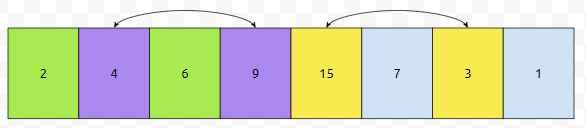
그러면 요렇게 바뀌겠군요. 그 다음에는 어떻게 할 거냐면요.

초록, 초록, 보라, 보라, 노랑, 노랑, 하늘, 하늘 이렇게 묶습니다. 이들이 증, 증, 감, 감을 따라가는지 보아야 합니다. 잘 따라가나요? 그렇기 때문에 2회전은 여기서 끝납니다.
그런데 아직 sort가 끝나지 않았어요. 한 회전을 더 돌려야 하기 때문입니다.

간격 4에서 출발합니다. 같은 색깔의 수가 증가해야 합니다. 이를 만족하지 않는 것이 있나요?

노랑하고, 하늘색은 만족하지 않네요. 따라서 이들을 swap 시켜야 합니다.
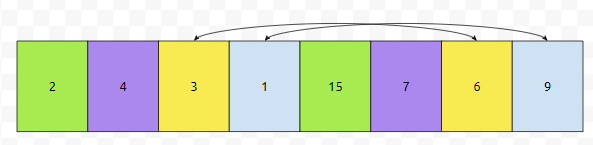
그러면 array가 요렇게 바뀝니다. 그 다음에 어떻게 하면 될까요?

초록, 보라, 초록, 보라, 노랑, 하늘, ... 이렇게 칠합니다. 같은 color는 무조건 증가해야 합니다. 증, 증, 증, 증이기 때문입니다. 이를 만족하지 않는 것이 어떤 것이 있나요?

4와 1, 그리고 15와 6이 있습니다. 둘을 change 하겠습니다.
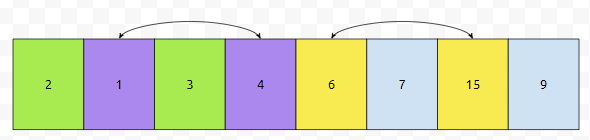
그러면 이렇게 되네요. 다음에 어떻게 할까요?
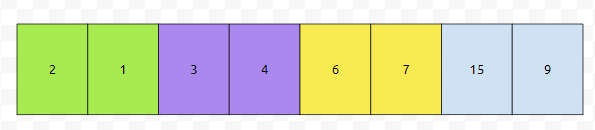
이렇게 색깔을 칠해봅시다. 이들은 모두 Up이 되어야 합니다. 이것을 만족하지 않는 color를 찾아 봅시다.

여기서, 그 조건을 만족하지 않는 것은 초록색하고 하늘색입니다. 이 둘을 swap 해 봅시다.

그러면 sort가 끝납니다. 시간 복잡도는 O(n(logn)^2)입니다. 이것만 보면 평범한 것처럼 보이는데.. 사실, 각 Cycle들의, 세부 과정들을 보면, 초록색, 보라색, 노란색, 하늘색을 나누었습니다. 이들 중에서 초록색에 대해서 먼저 수행을 하나, 노란색에 대해 먼저 수행을 하나, 보라색에 대해서 먼저 수행하나 결과값에 영향을 주지 않습니다.
따라서, 이 부분을 병렬로 수행이 가능합니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| leetcode 338 counting bits : 마지막 켜진 비트만 알면 된다. (6) | 2019.11.22 |
|---|---|
| 바빌로니아 법 알고리즘 : 어떻게 sqrt 함수를 구현할까요? (11) | 2019.11.20 |
| 피보나치 수열 : 왜 깡재귀로 구하면 지수 복잡도일까? (9) | 2019.10.30 |
| 그리디 알고리즘 : 매 순간 최적의 해를 선택한다. (6) | 2019.10.26 |
| 셀 정렬 : 갭을 줄여가면서 해결한다. (8) | 2019.10.14 |


최근댓글