포인터의 증감 연산을 간단하게 다루어 보도록 하겠습니다.
포인터 변수의 값 + 값
먼저, 이 경우부터 보도록 합시다. 아래 프로그램을 생각해 봅시다.

int형 변수 a가 선언되었습니다. 그리고 p는 int형 포인터 변수입니다. p는 a의 주솟값을 가지고 있어요. 그러면, p, p+1, p+2는 각각 어떤 값이 나올까요?

4만큼 차이나는 것을 볼 수 있어요. p+1은, p로부터 4바이트, p+2는 p+1로부터 4바이트만큼 증가한 것을 볼 수 있는데요. 자료형의 크기만큼 더했다는 것을 볼 수 있어요. long long형이면 어떨까요?

sizeof(long long)의 값도 같이 출력해 봅시다.
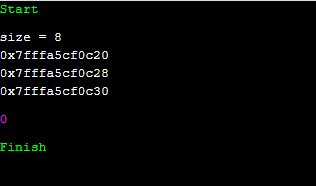
처음에 size = 8이 나왔습니다. 해당 환경에서, long long형은 8byte만큼 차지한다는 의미입니다. 이제, p, p+1, p+2의 차이를 봅시다. 8인가요? 0c28과 0c30의 차이는 2가 아니라 8임을 유의하세요. 16진수로 표현이 되어 있기 때문입니다. 그러면, 포인터 변수 + 값의 의미가 어느 정도 정리가 되시나요?
p + v = p의 주솟값 + v*(p가 가리키고 있는 data형의 크기)
뭔가 어렵네요. 조금 더 쉽게 풀어 볼까요? 노란색으로 칠한 부분을 풀어서 써 봅시다. 배열은 기준 주솟값에서부터 연속적으로 할당이 되어 있는 자료구조입니다. 그러면, p가 가리키고 있는 data 형이 T개 모여있는 배열 arr이 있다고 하면, arr은 data형 배열이에요. 그런가요?

그러면 p+v는 &(p[v])랑 같다는 것을 알 수 있어요. 이해가 안 가신다면, 형광펜으로 칠한 부분만 일단 외워두세요. 기준점으로부터 몇 단위만큼 이동하느냐는, 배열에서 제일 중요한 주제이기도 합니다.
그러면 v가 음수인 경우에는 어떨까요? 이것도 크게 어렵지는 않습니다.

위 코드를 실행해 봅시다. 어떻게 결과가 나올까요?
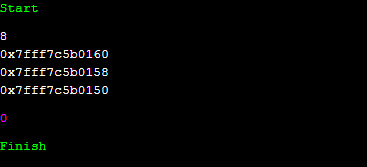
p와 p-1, p-1과 p-2가 각각 8이나 차이가 납니다. 그런데 감소하고 있어요.

그림으로 그려보면 이런 상황인데요. 하나의 원소당 8byte를 차지하고 있어요. 그러면 p-1은 p가 가리키는 원소의 이전 주소를, p-2는 p가 가리키는 원소의 이전의 이전 주소를 의미합니다. 그렇기 때문에 p-2의 값은 p에 비해 16만큼이나 작습니다.
이제 포인터 변수끼리 뺄셈을 하면 어떤 값이 나오는지를 봅시다. 생소해 보이는데, 사실 생각보다 많이 씁니다. 예를 들자면, 아래와 같은 코드는, 정렬된 배열에서 2보다 같거나 큰 최초의 위치를 구하는 코드입니다.

lower_bound의 리턴값은 iterator입니다. 그냥 쉽게 주솟값을 가리킨다고 생각하시면 됩니다. 이 프로그램의 결과 값은 1이 나옵니다. arr[0] < 2이고, arr[1] >= 2이고, arr이 오름차순으로 정렬이 되어 있으니까 당연해 보이기는 하는데. 어떻게 된 것일까요?
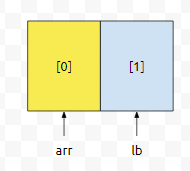
lower_bound의 리턴 값을 lb라 합시다. lb는 arr의 주솟값에 4를 더한 값입니다. &(arr[1])입니다. 그런데, lb는 arr+1과 같습니다. arr+1에서 arr을 빼면 1입니다. 맞나요?
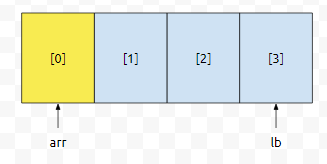
만약에 lb의 값이 &(arr[3])이였다면 어떨까요? 그러면 lb는 arr+3과 같아요. lb의 주솟값은 arr + 12가 될 거고요. 그러면 lb - arr은 어떤 값이 나올까요? (arr + 3) - arr = 3이 나옵니다. 포인터 형이 같은, 두 포인터 변수 p와 q가 있습니다. p의 주솟값이 q의 주솟값보다 작거나 같다고 해 봅시다.
그러면 q-p의 값은 무엇을 의미할까요?

q가 p로부터 몇 단위만큼 떨어져 있는지를 의미합니다. 여기서 1 단위는, p와 q가 가리키고 있는 data 형의 크기입니다.
'코딩 > C' 카테고리의 다른 글
| c언어 const 포인터 : 어디에 붙는지에 따라 해석 방법이 다르다. (8) | 2019.11.11 |
|---|---|
| 상수 포인터 == 배열? 잠깐 짚고 넘어갑시다. (3) | 2019.11.01 |
| 구조체 포인터 변수 : pointer만 알면 다른 건 똑같다. (7) | 2019.10.24 |
| c언어 swap 함수 : 포인터 변수를 이용해서 구현해 봅시다. (6) | 2019.10.18 |
| c언어 포인터 변수 : 주솟값을 저장한다. (11) | 2019.10.11 |


최근댓글