tree dp는 최근에 코테에 나왔습니다. 그래서 트리 dp 2 문제를 준비해 보았습니다. 스크루지 민호 시리즈는 이들을 연습하기 좋은 셋트이기 때문입니다. 트리 탐색이나, dfs에 대한 기본적인 이해가 있다고 가정하고 진행하겠습니다.
먼저, 이 문제부터 보겠습니다. 왜 1부터 안 푸냐. 사실 해당 방법으로 풀기는 2가 1보다는 쉽기 때문입니다.

트리가 이렇게 있어요. 문제 조건을 잘 보시면, 양방향 간선에 연결되어 있는 도시 2개 중에 최소 하나 이상은 경찰서가 있어야 함을 알 수 있어요. 그러면 현재 cur에 경찰서를 세운 경우와 그렇지 않은 경우로 나눌 수 있음을 알 수 있어요.

먼저, cur에 경찰서를 세우지 않은 경우를 생각해 봅시다. 그러면, 자식 도시들은 모두 경찰서를 세워야 합니다. 만약에 자식들 중 어느 하나라도 세우지 않았다고 해 봅시다.

그러면 감시가 안 되는 도로가 생기게 됩니다. 따라서, 현재 cur에 경찰서를 세우지 않았다면, 자식 노드 모두에게 경찰서를 세우면 됩니다. 이를 dp[0][cur]라고 하겠습니다.
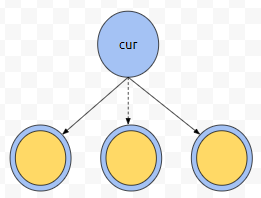
만약에 경찰서를 세웠다면 어떨까요? 이 경우에는, 자식들은 세우거나, 안 세우거나 둘 중 하나임을 알 수 있어요. 안 세워도 도로를 감시하는 데에는 문제가 없음을 알 수 있어요. 그러면, dp 테이블은 어떻게 하면 될까요? dp[상태][위치]로 잡으면 됩니다.

dfs 함수에서 dp를 어떻게 채우는지 봅시다. 먼저, 11번째 줄에 cc 값이 0이라는 것은 leaf라는 의미입니다. 리프에 경찰서를 세우지 않았아면 0, 세웠다면 1을 리턴하게 하면 됩니다. 어? 그러면, 도시가 하나만 있을 때 어떻게 처리하나요? 라고 물어보실 수 있는데요. 하나만 있을 때에는 단순하게, 경찰서가 있는 경우만 돌려주면 됩니다.

다음에, 리프가 아니라면, 해당 위치에 건물을 세운 경우와, 그렇지 않은 경우를 나누어서 생각하시면 됩니다. 여기서 알아보기 쉽게 리팩토링을 하면 z0 대신에 z01로 해도 나쁘지 않을 듯 합니다. 자식들의 상태가 0 또는 1이 될 수 있기 때문입니다. 이것과 거의 비슷하게 접근할 수 있는 문제 중에는 2021 카코테 7번이 있습니다. 참고하시면 좋을 듯 싶네요.
이 문제는 어떨까요? 이 문제를 굳이 tree dp로 풀려면 약간의 생각이 필요합니다.
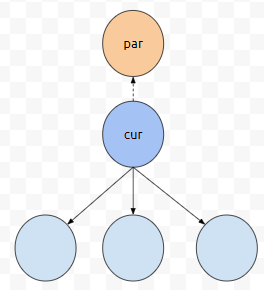
예를 들어, 우리가 cur에 대한 어떠한 정보들을 알고 있을 때, 자식들에 대한 어떠한 정보를 잘 채워야 한다고 해 봅시다. 어떤 정보들을 채워야 할까요?

cur의 어떤 정보들을 토대로 c2의 어떤 정보들을 채워야 한다면. 일단, c2에서부터 leaf까지 최대 거리는 dfs 1번으로 구할 수 있습니다. 문제는, 제가 군청색, 주황색으로 칠한 부분들입니다.

이 부분입니다. 사실 이들을 구하는 것이 다라고 할 수 있어요. 그런데, 주황색 부분은 크게 어렵지 않습니다. 이렇게 생각하면 되기 때문입니다.

단지, c2에서 주황색 부분들까지의 최대 거리는 cur에서 주황색 부분들까지의 최대 거리 + 1을 하면 되기 때문입니다. top[x]를 x로부터, x의 서브 트리가 아닌 노드까지 거리 중 최댓값이라고 해 봅시다. top[cur]를 알고 있을 때 top[c2]를 어떻게 구할까요? 일단, c2에서 주황색 부분까지 거리 중 최대치는 단순하게 top[cur] + 1로 구할 수 있습니다. 그런데, 그 경우만 있지 않습니다. 군청색까지의 거리도 고려해야 합니다.

그런가요? 즉, 우리는 군청색 부분의 최댓값을 구해야 합니다. 자식이 바뀔 때 마다 이 값을 빠르게 계산하려면 어떻게 하면 될까요?

단지, 벡터 배열 2개를 더 선언하면 됩니다. dp_left와 dp_right인데요. dp_left[i][x]를, i의 [0, x)번째 자식들의 dp 값 중에 최대치로, dp_right[i][x]를 i의 (x, i의 자식 갯수-1]번째 자식들의 dp 값 중 최대치로 정의하시면 됩니다. 이 둘을 채워 봅시다.

중요하게 보아야 할 점은, dp_left에 먼저 넣고, dp[next] + 1과 mmx의 최대치를 mmx에 반영시킨다는 것입니다.

이는 dp_right도 마찬가지인데요. 51번째 줄에 reverse가 들어간 이유는 거꾸로 넣었기 때문입니다.

dp[x]는 x로부터 x의 자식들 중 거리의 최댓값이라 정의 했으므로, dfs를 위와 같이 돌리면 됩니다. 스크루지 2보다 dp 식이 복잡한데요. 고려해야 할 것이 많고, 위로 올라가서 내려가는 것 등을 고려해야 하기 때문입니다. 두 문제의 공통점은 부모의 상태를 알고 있을 때, 자식들의 상태를 어떻게 빨리 채울까? 혹은 자식들의 상태를 알고 있을 때 어떻게 부모의 상태를 빠르게 채울까 입니다. 그것을 위해서 적절한 처리를 하거나, 자료구조가 들어간다는 점을 파악하시면 좋겠습니다.
사실 코테에서 이 정도까지 나올 일도 잘 없을 듯 합니다. 그리고 이렇게 접근을 했다면 더 쉬운 풀이가 있을 겁니다. 실제로 스크루지 1은 이것보다 훨씬 쉬운 풀이로 푸신 분들이 있습니다. 만약에 저게 정해라면, 풀지 않아도 합격할 겁니다. 그렇지만, 익혀 두시는 것도 나쁜 선택이 아닐 거라 생각합니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 기하 문제를 다룰 때 잘 써먹게 되는 radian degree 변환을 알아봅시다. (2) | 2021.05.16 |
|---|---|
| 왜 위상 정렬을 이용하면 그래프 사이클이 있는지 판단할 수 있을까요? (2) | 2021.05.03 |
| 백준 배열 돌리기 5 : 전략적인 브루트 포스로 풀어봅시다. (0) | 2021.04.04 |
| 알고리즘 시간 복잡도 대강 분석하는 방법을 예제를 통해 알아봅시다. (0) | 2021.04.03 |
| 여러 트릭에 응용되는 트리에서의 dfs ordering을 알아봅시다. (0) | 2021.03.07 |


최근댓글