어떠한 수가 배열 내에 있는지를 빠르게 찾고 싶습니다. 그럴 때, 이진 검색, binary search를 이용할 수 있습니다. 그런데, 전제 조건은 정렬이 되어 있어야 한다는 것입니다. 왜 그럴까요? 정렬이 되어 있지 않다고 해 봅시다.

중앙에 있는 3을 기준으로 9는 왼쪽에 있고 오른쪽에 없을 수도 있어요. 그러면 3을 기준으로 왼쪽에서 찾아야 합니다. 그런데, 이런 경우도 있을 수가 있어요.

중앙에 있는 3을 기준으로 좌측에 없고, 우측에 있다. 이런 경우는 또 어떤가요? 내가 있는 위치를 기준으로 9가 왼쪽에 있을 수도 있고, 오른쪽에 있을 수도 있고, 없을 수도 있기 때문에, 현재 탐색하는 위치를 기준으로 절반씩 해를 좁혀나갈 수가 없어요. 따라서, 선형 탐색으로 해결을 할 수 밖에 없을 거에요.
물론, hash를 이용하는 방법도 있긴 하지만, 충돌이 많이 나면 힘듭니다. 이에 대한 것은 자료구조 시간에 다시 언급을 하도록 하겠습니다. 이진 검색을 하기 위한 전제 조건은 데이터가 정렬 되어 있어야 한다는 것입니다.
오름차순으로 정렬된 배열이 다음과 같이 있습니다.
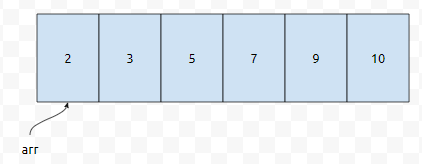
여기서 우리는 10을 찾아보겠습니다. 배열의 크기가 6이기 때문에, s는 0번째 원소인 2를, e는 5번째 원소인 10을 가리킵니다. mid는 [(s+e)/2]로 계산이 됩니다. [(0+5)/2]는 2입니다.
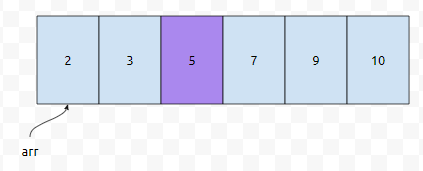
그렇기 때문에 arr[mid]의 값은 5입니다. 내가 찾을려는 값 10은 5보다는 큽니다. 따라서 보라색을 기준으로, 우측에서 탐색합니다. 즉, s가 3, e가 5가 됩니다.

그러면 mid는 어떻게 계산이 될까요? [(3+5)/2] = 4입니다. 따라서 보라색으로 칠한 부분이 중간이 될 거에요.
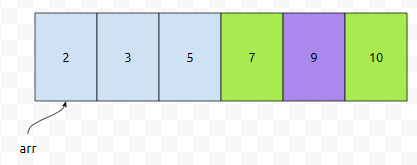
제가 찾을려는 10은 9보다는 큽니다. 따라서 우측에서 탐색해야 할 겁니다. 즉, 3회전 때에는, 노란색으로 칠한 구간만 탐색을 하면 됩니다.

초록색으로 칠한 부분은 9보다 작거나 같다는 것이 자명합니다. 오름차순으로 정렬이 되어 있기 때문입니다. 그런데 10은 9보다 큰데, 9보다 작거나 같은 원소들이 있는 위치에 있을 리가 없을 거에요. 따라서 노란색으로 칠한 부분을 탐색합니다.
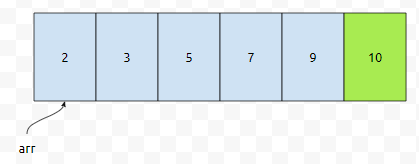
s가 5, e가 5입니다. mid의 값도 5입니다. arr[5]의 값은 10입니다. 우리가 찾을려고 하는 값을 찾았습니다. 따라서, 10을 찾았다고 하면 됩니다. 이제 같은 배열에서 6을 찾아봅시다.
일단 이 부분까지는 같을 겁니다.

찾으려고 하는 수 6은 9보다는 작습니다. 따라서 보라색으로 칠한 부분의 왼쪽 부분인 노란색으로 칠한 구간을 탐색해야 할 겁니다. 따라서 s = 3, e = 4-1 = 3이 됩니다.

s = 3이고 e = 3입니다. 그러면 mid의 값도 3일 겁니다. arr[3]의 값은 7입니다. 제가 찾을려는 값인 6은 이것보다 더 작습니다. 따라서 왼쪽에서 탐색을 해야 할 거에요. e = mid-1로 바뀝니다.

e>s입니다. s<=e가 아니기 때문에 찾지 못했습니다. 따라서 찾지 못했다는 표시를 합니다. 보통 이 경우 -1을 리턴하는 게 일반적입니다만, 문제에 따라서 다를 수 있으니 센스있게 처리를 잘 하시면 좋겠습니다.
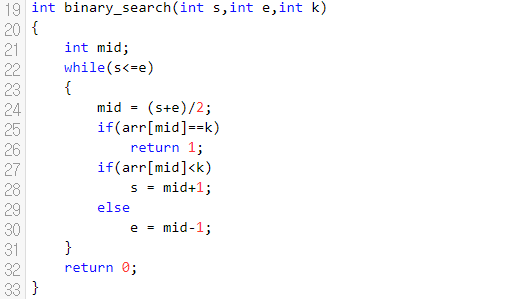
백준 10815번 문제는, 어떠한 배열에 특정한 수가 존재하면 1을, 아니면 0을 출력해야 합니다. 배열을 정렬한 다음에 각 쿼리마다 binary_search 함수를 호출할 건데요. s<=e인 경우에만 재귀 호출이 들어간다는 것을 알 수 있어요. 그리고, 구간의 중간을 기준으로 왼쪽에서 탐색할 것인지, 우측에서 탐색할 것인지를 정하고 있는데요. 찾으려는 수 k가 arr[mid]보다 큰 경우 우측에서, 작다면 좌측에서 찾습니다.
만약에 같다면 찾았다고 리턴해 버리고 있어요.
그러면 내림차순이던 오름차순으로 정렬된 배열에서 중간에 있는 값을 기준으로, 중간 값이 찾으려는 값이 아니라면 왼쪽이나 오른쪽 중에서 한 부분만 보면 될까요? 오름차순으로 sorting 되었습니다. 그리고, 중간 값이 M이라고 해 봅시다. M과 다른 값, 그러니까 제가 찾을려는 값 m이 중간을 기준으로 왼쪽, 오른쪽에 다 있다는 명제를 p라 하고, 이게 참이라 해 봅시다. 즉, 명제 p가 참이라고 해 봅시다. 뭔가 많이 보던 증명 방법인 거 같은데, 중학교 때 배운 귀류법이에요. 모순에 의한 증명법이라고 흔히 이야기 하는데요. root(2)가 유리수가 아니라는 것을 prove 하라는 것은, 한 번 쯤 교과서에서 보셨을 문제입니다.

M!=m이기 때문에 m<M이거나, M<m입니다. 첫 번째 경우, 우측에 있는 m이 M보다 작습니다.

제가 칠한 빨간색 부분 때문에 오름차순으로 정렬되지 않았습니다. 만약에 M<m이라면 어떨까요?
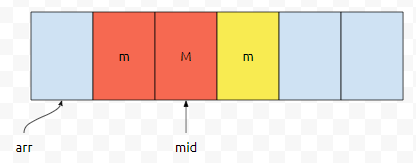
이번에도 빨간색으로 칠한 부분 때문에 문제가 됩니다. m이 M보다 크기 때문입니다. 명제 p가 거짓입니다. 그렇기 때문에 not p가 참이 됩니다. not p는 무엇인가요? 중간 값을 기준으로, 중간 값과 다른, 제가 찾을려는 값 m이 중앙을 기준으로 왼쪽, 오른쪽에 동시에 존재하지 않는다입니다.
따라서 정렬이 되어 있을 때 반씩 후보해를 좁혀나가는 방법이 옳습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 부분합 구하기 : 누적합만 들고 있으면 된다. (8) | 2019.07.21 |
|---|---|
| 계수 정렬 (counting sort) : 특정 숫자의 빈도를 센다. (2) | 2019.07.20 |
| 선택 정렬 알고리즘 : 가장 우선 순위가 높은 것을 매 턴마다 찾는다. (2) | 2019.07.17 |
| stable sort : 우선 순위가 같은 데이터들은 어떻게 정렬될까요? (4) | 2019.07.14 |
| 삽입 정렬 알고리즘 : 원소가 들어갈 위치는 어디인가? (2) | 2019.07.11 |


최근댓글