Hash에서, 면접에서 물어볼 만한 키워드들을 천천히 알아보도록 하겠습니다. 이 중 오늘은 재해싱에 대한 이야기를 간단하게 하고 넘어가겠습니다. Hash Table은, 저번시간에 배운 바로는, 버킷에다가, 데이터를 주렁 주렁 매달아 놓는 식으로 많이 처리를 한다고 했었습니다. 보통, Chaining을 사용하는 경우, List를 사용한다고 했었습니다.
저는 간단하게 구현하기 위해서, 2차원 배열로 구현을 했었고요. 그런데, 생각을 해 봅시다. 수가 2개만 들어왔어요. 그런데, 1000만개의 바구니를 미리 만들어 놓을 필요가 있을까요? 2개를 위해서, 1000만개의 바구니를 생성한다. 이것만큼 낭비가 없습니다. 그러면, 어떻게 할 거냐. 초기 사이즈를 매우 작게 잡습니다.

예를 들자면, 2개의 초기 bucket 사이즈를 잡을 수 있을 겁니다. 그러면 hash 값이 들어오면, 이것을 어떻게 넣을까요? 가장 간단한 방법은 hash value에 버킷의 갯수를 나눈 나머지를 취하는 것입니다. 예를 들어서 hash value, 줄여서 hv라고 하겠습니다. hv가 5라면 [1]에다가, 8이라면 [0]에다가 넣습니다.
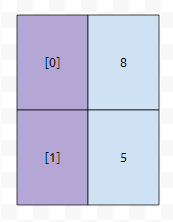
그러면 이렇게 들어갈 겁니다. 그런데, 테이블에 있는 데이터의 수가 20만개 정도 되는데 바구니 수가 단 2개라면 어떻게 될까요? 그러면, 최소한 10만개의 데이터가 들어가는 방이 최소한 하나 이상 존재할 겁니다.
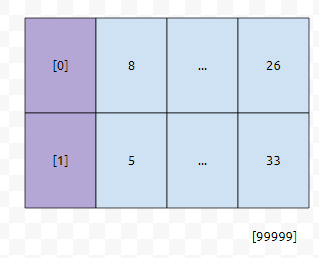
예를 들어, 10만, 10만으로 분할되었다고 가정하면, 평균적으로 어떠한 Key값을 찾기 위해서, 50000개의 요소들을 보아야 합니다. 직관적으로 생각해 보아도, 이는 엄청난 낭비임을 알 수 있어요.
그러면 버킷이 b개, 키가 n개 있는 경우, 시간 복잡도는 어떻게 될까요? 그런데, 평균 시간 복잡도는 계산 하기가 상당히 빡세 보입니다. 그러면, 어떻게 해 볼까요? 최선의 경우에 어떻게 굴러갈 지 구해 봅시다. 일단 우리는 각 격자에 수를 하나씩 써 볼 겁니다. 아래 그림과 같이 말입니다.
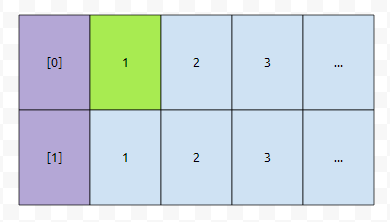
그러면, 이들은 무엇을 의미할까요? 각 hv값에 대응되는 버킷 번호를 따라 탐색을 할 때, 몇 개의 요소를 검사해야 find가 되는지 나타낸 겁니다. 예를 들어 [0]번에 5, 7, 3이 있었다고 합시다. 그러면 5는 [0]번의 1번째에 있기 때문에, 1번의 요소 검사를 해야 합니다. 3은 3번 검사해야 하고, 7은 2번 검사해야 합니다.
그러면 1번째의 경우, [0]을 택하던, [1]을 택하던 1이라는 숫자밖에 택할 수 밖에 없을 겁니다.
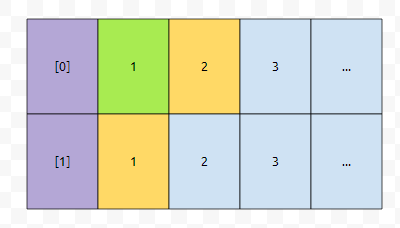
다음에는 어떤가요? 2를 택하던지, 아니면 1을 택하던지 둘 중 하나입니다. 그런데 2를 택하면, 우리가 택한 원소들을 탐색하기 위해서 search 하는 총 비용이 3이 될 겁니다. 이득이 되지는 않습니다. 따라서, 1이라고 표시된 것을 택합니다.
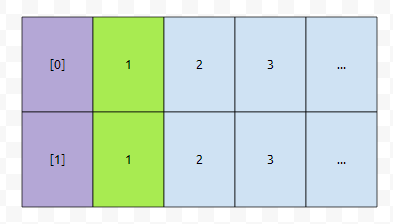
그러면 요래 선택을 할 수 있을 겁니다. 그 다음에는 어떤 것을 선택해야 하나요? 2와 2를 선택할 수 있습니다. 이 둘 중에는 아무거나 선택해도 될까요?

그렇기 때문에, 아무거나 select가 됩니다. 다음에는 2와 3 중에 골라야 하는데요. 3보다는 2가 작습니다. 따라서, 2를 골라야 겠군요. 그러면 아래와 같이 표시할 수 있습니다.
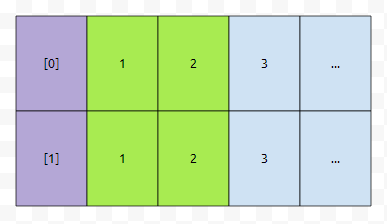
이는 우리가 아래와 같이 선택한 것보다 총 cost가 작음을 알 수 있어요.
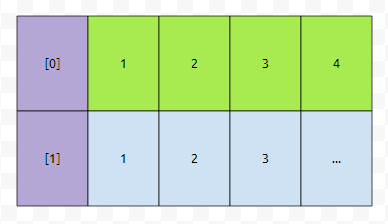
초록색 부분의 합은 위의 그림의 6보다 큰 10입니다. 그런가요? 따라서 거의 골고루, 바구니를 선택하는 게 optimize 한 해일 겁니다. 이 점에 주목을 하면, 버킷이 b개가 있고, key가 n개가 있는 경우, 아래와 같이 selected 되는 것이 최적일 겁니다.

이 때, 초록색 부분만 봐도, 최소한, 평균적으로 약 1/2*n/b회 가량의 탐색을 해야 한다는 것을 알 수 있어요. 즉, n이 매우 클 때, b가 작다면 hash table을 쓰는 의미가 없습니다. 따라서, 버킷의 갯수에 비해서, 해시 테이블에 들어간 키의 갯수가 커지면, 바구니의 갯수를 늘리는데요. 이 과정에서 재해싱이 일어납니다.
이 과정을 간단하게 언급해 드리고, 같은 아이디어를 이용해서, 평균 복잡도도 간단하게 계산해 봅시다.
그러면 reHashing이라는 게 무엇인가? 간단합니다. 단지, 어렵게 배우셔서 어려워 보일 뿐.
먼저 아래와 같이 테이블이 있다고 생각해 봅시다.

여기서 재해싱이 되면, 먼저, 새로운 테이블이 생성이 됩니다. 그리고 연결이 되어 있는 hash value의 값이 [0]번은 4,6이였고, [1]번은 3이였는데요. 이들이 들어갈 버켓 번호가 재계산이 됩니다. 보통, 이 값은 해시값에 바구니 갯수를 나눈 모듈러를 취하는 경우가 많은데요.

그러면 위 그림과 같이 다시 테이블이 구축이 될 겁니다. 이 때 복잡도는 O(size)가 됩니다. 생각보다 상당히 무거운 연산이기 때문에, 이 연산은 자주 일어나지는 않는데요. Key값의 갯수/바구니 갯수의 값이 일정 수치 이상 커지면 재할당이 일어납니다.
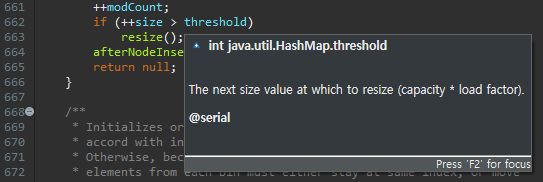
HashMap의 putVal 함수를 보면, threshold보다 size가 크면, resize를 호출하고 있어요. 이것은, 다시 재해싱을 하는 함수입니다. Java에서는 기본적으로, 이 값이 0.75임을 알 수 있어요.

즉, 버킷 갯수가 10만개일 때, key가 7.5만개 이상 들어가면 다시 확장한다는 소리입니다. 그러면 skew, 그러니까, 특정한 곳에만 쏠리는 현상이 resize가 되면 해결이 될 수 있는가? 를 물어보신다면, 그건 아닙니다. 아닌데, 왜 그렇게 하느냐고 물으신다면, 평균 탐색, 삽입, 삭제 시간을 낮추기 위해서 한다고 답변하시면 됩니다.
그러면 avg cost는 어떻게 구해야 할까요?
아까 봤던 그림을 다시 끌고 오겠습니다.

사건을 하나 정의할 건데요. 저는 n회의 시행을 할 때, 버킷만 선택할 겁니다. 그러면 어떻게 되냐면, 선택을 안 한 가장 작은 번호를 뽑습니다. 이 확률은 1/b로 모두 같습니다. 먼저, 첫 번째 경우는 <1, 1, 1, 1> 중 하나를 뽑을 겁니다. 이 부분은 그리 어렵지 않아요.
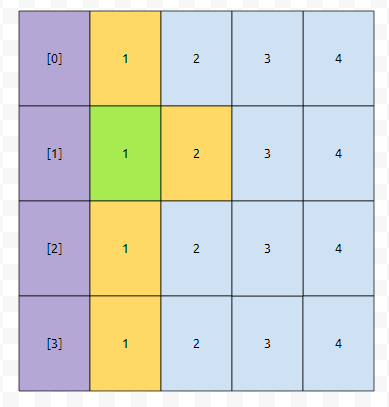
다음에는 어떤가요? <1, 2, 1, 1> 중 하나를 뽑을 겁니다. 만약에 2를 뽑았다면, 1번과 1번을 선택한 셈이 됩니다. 그렇지 않다면, 첫 번째 요소는 1번에 들어갔지만, 2번째는 1번이 아닌 다른 곳에 들어갔다는 것이고요.

1번을 또 select 했다고 합시다. 그 다음에 <1, 3, 1, 1> 중 하나를 뽑을 겁니다. 그런데 1번, 3번 순으로 바구니를 뽑은 경우에는 어떤가요? 이 때의 상황을 그림으로 그려 봅시다.

<1, 2, 1, 2> 달라 보일 수도 있겠지만, <1, 3, 1, 1>에 쓰여져 있는 수들의 합과 같습니다. 이는, 어떠한 버킷에서 하나의 수를 뽑으면, 그 위치에 있는 다음 수를 뽑게 되어 있기 때문입니다. 어떠한 경우라도. 그러면 이 노란색에 있는 수들은, 직관적으로 보았을 때, 현재 초록색의 키들이 추가되어 있는 상태에서, 다시 add 연산이 일어났을 때, 몇 회의 check를 해야 하는가? 를 의미합니다. 그 수들의 합에 b를 나눈 값이 되는 셈입니다.
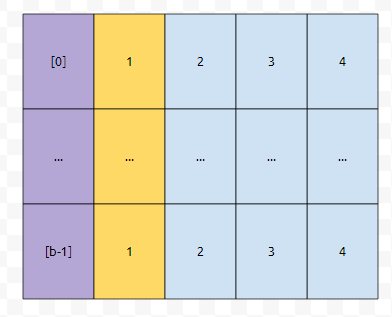
그러면 처음에는 평균이 b/b이니 1, 하나를 선택하면 그 다음에는 어떻게 될까요?

(b+1)/b가 될 겁니다. 3번째로 선택할 때에는 (b+2)/b. 이런 식으로 n개의 수를 넣으면, 기댓값들의 합을 계산해 보면, 대충, b/b + (b+1)/b + ... + (b+n)/b가 될 겁니다. 이것을 n으로 나누면 어떻게 될까요? 계산해 보면, (nb + n(n+1)/2)/(nb)인데요. 상수항 날려버리면 대충 O(n/b)가 나옴을 알 수 있어요.
그런데, 어떠한 수를 Hash에서 찾지 못한 경우도 있을 텐데. 이 경우는 또 어떨까요? 마찬가지로 생각해 봅시다. n번을 select 했어요.

그러면 이런 식으로 그려질 거에요. 어떻게 선택했던지 간에, 노란색의 합은 b+(n-1)로 같습니다. 이를 b로 나누면 1+(n-1)/b가 되고, 이는 O(n/b)로 표현할 수 있습니다. n에 비해, b가 굉장히 작다면 평균적으로 따졌을 때에도 비효율 적이기 때문에, 키가 일정 이상 들어가면 버킷 수를 키웁니다. 그럼으로서, 평균 복잡도가 상수가 되게끔 해 주는 겁니다.
이 정도만 기억하시면 좋겠습니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| LRU 알고리즘 : 리스트를 활용해서 구현해 봅시다. (6) | 2019.09.23 |
|---|---|
| 평방 분할 (Sqrt Decompositon) : 루트로 쪼개보자. (2) | 2019.09.22 |
| 자료구조 해시 테이블 : 직접 구현해 봅시다. (8) | 2019.09.11 |
| 자료구조 덱 (deque) : 앞과 뒤에서 추가되고 삭제된다. (2) | 2019.08.22 |
| 비둘기집의 원리 : 왜 해시충돌을 피할 수 없는가? (4) | 2019.08.17 |


최근댓글