코딩 테스트를 보기 위해서는, 기본적으로 제한 조건을 읽을 줄 알아야 합니다. 단순히 n이 30보다 작고 m이 15보다 작은 조건이 들어오는군이 아니라, 왜 출제자가 이런 조건을 주었는지 곰곰히 생각해 보자는 것입니다. 이게 그렇게 어렵지 않은 것 같지만, 저는 솔직히 쉽지 않았습니다. 문제를 읽고 바로 이거네? 하고 들어가는 습관이 있다 보니, 이런 세세한 조건을 놓치는 경우가 다반사였습니다.
코테에서 이런 일이 발생했다면 탈락하실 확률이 높아집니다. 왜 제가 코테에서 물을 많이 먹었는지 단박에 알 수 있는 무서운 말입니다. 사실 조언해 줄 실력도 못 되지만, 작년에 물을 많이 먹으면서 제가 부족했던 점을 복기해 보았습니다. 그렇게 생각해 주시면 좋을 듯 싶습니다. 자. 그러면 어떻게 조건을 분석해야 하는지, 플레 5정도 되는 문제인 백준 1742번을 보도록 하겠습니다. 개인적으로는 TSP보다는 1단계 어려워 보입니다. 그러니 그 난도가 적당한 듯 싶긴 합니다. (이건 어디까지나 제 의견일 뿐) 인간적으로 다이아 이상의 문제는 어렵기 때문에 이 정도 난이도로 연습해 봅시다.

어떻게 풀어야 할 지 창을 닫고 20분 정도 생각해 보세요. 사실, 쉬운 문제는 아니긴 하지만, 고민해 볼 가치는 있습니다.
고민을 해 보셨나요? 아마 이렇게 읽으신 분들도 꽤 계실 거라 생각이 듭니다. 어느 정도 코딩 테스트를 준비하기 위해서 알고리즘 문제를 풀어 보셨고, 위상 정렬에 대해서 아시고, 1005번 문제도 풀어보셨다면 말입니다.

동의 하시나요? 입력에 들어온 a b 쌍에 대해서 읽고, N, M에 대한 범위 읽고 순서가 있으니까 위상 정렬을 생각하셨을 거고, 아마 여기까지만 읽으시고 topology sort에 dynamic programming을 섞어야 겠거니. 이렇게 생각하셨을 거에요. 이렇게 생각하시지 않으셨나요? 그렇다면 다행입니다.
왜 이런 이야기를 했냐면, 사실 제가 처음에 이렇게 생각했기 때문입니다. 여기까지 읽어 내신 것만 해도 좋습니다. 그러면, 대충 정점이 10만개, 간선이 5만개 정도 되는 그래프가 있습니다. 이 때, 위상 정렬의 가짓수를 어떻게 구하실 건가요? 역시 생각을 많이 해 봐야 할 듯 싶습니다. 몇 분 정도 고민해 볼까요?
고민을 해 보셨나요? 생각보다 문제가 단순하지 않고, 굉장히 어렵고 까다로워 보입니다. 네. 맞습니다. 조건을 대충 봐 버리면, 굉장히 어려운 문제가 되어 버립니다. 그런데 백준에서 16명이나 풀어버렸습니다. 이 분들은 어떻게 푸셨을까요? 다시, 문제를 봅시다. 이번에는 제한 조건의 숫자와 키워드에 주목하면서 보도록 합시다. 이는 문제가 이런 시간 복잡도로도 풀릴 수 있겠네? 라는 Hint를 주기도 하기 때문입니다.

N과 M조건에 밑줄을 칩니다. 게다가 M의 최댓값은 많아봤자 15입니다. 2의 15승이 32768이다라는 것을 생각해 보면, 이는 굉장히 매력적인 힌트 중 하나가 될 수 있습니다. a가 b를 이긴다는 관계가 있으면 무조건 위상정렬로 풀어야 한다는 생각을 깰 수도 있는 범위이기 때문입니다.
일례로 외판원 순회 문제 또한, 도시 수가 15, 16, 17, 심지어 20일 때도 무난하게 돌아갔다는 것을 알 수 있습니다. 그렇기 때문에, N의 최댓값이 30이다, M의 최댓값이 15다. 그러면 그냥 밑줄만 치지 마시고, 형광펜이든 무슨 펜이든 매우 중요하다는 강조 표시를 해 놓으면 도움이 됩니다. 30이면, 30/2 = 15이기 때문에, meet in the middle 이라는, 반씩 쪼개서 해결하는 기법을 시도해 볼 수도 있기 때문이에요. 일례로 백준 2552번 같은 경우에는, 전구 갯수가 30 이하이기 때문에 반씩 쪼개는 기법을 시도해 볼 수 있습니다. 그러면 이것을 토대로 생각의 흐름을 써 보도록 하겠습니다.

이전 생각의 흐름과 달라진 부분이 눈에 들어오시나요? 일단 위상 정렬에 대해서 물어보는 문제일 수도 있겠는데? 가 다릅니다. 그냥 이 문제는 위상 정렬이야. 하고 단정짓는 것과는 다르다는 것을 알 수 있어요. A일 수도 있겠는데? 와 A야! 는 뉘앙스 자체가 다릅니다. 후자는 '~는 A다' 라는 관점에 고정되어 있습니다. 전자는 그렇지는 않아요. A일 수도 있지만, B일 수도 있고, C일 수도 있어요. 관점이 고정되어 있지 않아요. 후자와 같이 생각했을 때에는 잘못된 풀이임에도 계속 그 풀이만 보고 있을 확률이 (제가 한) 경험상 더 높아요.
다음, 2번째 문단을 보면, N과 M의 범위가 나와 있습니다. 이 부분에서 제가 3개의 문장으로 무엇을 써야 하는지를 간략하게 분석을 했는데요.

M개의 결과. 이걸 해석을 했더니, 한 Component당 많아봤자 16개의 노드만 속해있을 수 있고, 그것에 대해서는 비트 마스크를 이용한 다이나믹 프로그래밍 기법으로 해결할 수 있다는 결론이 나왔습니다. 제일 중요했던 조건이 무엇이였나요? M이 15 이하라는 것입니다. 이 놓치기 쉬운 조건을 얼마나 잘 보았느냐가 문제를 풀고 못 풀고를 갈랐던 셈입니다. 최소한, 문제를 보는 시야를 넓힐 수 있었던 셈입니다.
큰 나무부터 보고, 조건부터 제대로 해석하는 연습을 하는 게 중요합니다. 그것을 얼마나 잘 보느냐에 따라서, 여러 가지 방법으로 시도를 해 볼 수도 있기 때문이에요.

이제, 조건으로부터 어떻게 풀어야 할 지 대략적으로 설계도만 그려 놓았습니다. n개의 Component가 있을 때는 일단 생각하지 말고, 1개의 Component만 있을 때만 가짓수를 어떻게 구할지 생각해 봅시다. 어짜피, 하나의 요소에 있는 노드의 수는 많아봤자 16개이기 때문에, 비트로도 충분히 상태를 표현할 수 있는 범위 내에 들어온다는 것을 알 수 있습니다.

요소가 다음과 같이 있다고 생각해 봅시다. 이 때 state는 15로 표현하면 좋겠어요. 0번, 1번, 2번, 3번 노드가 있기 때문이에요. (1을 0번, 2를 1번, 3을 2번, 4를 3번이라 이야기 합시다.) 이 때, 1을 먼저 순서에 넣으면 어떻게 되나요?

이 때는 2, 3, 4만 남게 됩니다. 즉, 상태 14가 됩니다. 그 다음에 2를 순서에 넣을 수 있나요?
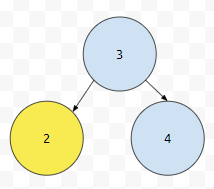
넣지 못합니다. 3을 먼저 넣어야 하는 조건이 있기 때문입니다. 그러면 어떤 상태가 있을 때, 1위가 될 수 있는 후보들을 빼는 경우들을 모두 고려해 주면 될 듯 싶습니다. 그런가요? 그러면, 위 그림에서 후보가 될 수 있는 것은 어떤 게 있을까요? 2번 (3이라고 써져 있는 무언가)입니다.

이 경우는 어떨까요? (1번이라고 써져 있는 무언가인) 0번과, (3번이라고 써져 있는) 2번입니다. 이들을 먼저 선택할 수 있어요. 그러면, dp 식을 다음과 같이 세우면 될 거에요.

이것을 토대로, 가짓수를 계산하는 함수를 만들어 보겠습니다.

먼저 calc 함수는 가짓수를 계산합니다. 이것은 lo를 받는데요. 요소 별로 번호를 압축해서 들어옵니다. vector vs에, 해당 요소가 가지고 있는 노드 번호들을 모두 저장해 버립니다. 예를 들어, 2, 3, 5번을 가지고 있으면 vs에 2, 3, 5를 넣습니다. 상태는 요소의 size만큼 있을 겁니다. 따라서, 처음 state는 (1<<요소의 size) - 1이 될 거고, 요소의 크기는 sz가 될 겁니다. 이제 work 함수를 봅시다.

일단, 기저 조건은 state가 0일 때, 즉, 아무 노드도 없을 때입니다. 이 때에는 가짓수를 1이라고 하시면 됩니다. 그렇지 않다면, in, 그러니까 서브 그래프에서 indegree를 저장하는 in 배열을 선언합시다. 아니면 i로 오는 간선의 갯수를 저장하는 in 배열이라 해도 좋겠군요.

먼저 72번째에 걸려있는 for문은, 부분 문제에서, 현재 있는 노드들에 대해서, 그 노드들과 연결된 간선이 있는지를 봅니다. 만약에 있다면, 그 간선의 종점의 in값을 1 증가시킵니다. 다음에 82번째 줄에 걸려있는 for문은 해당 노드가 사용이 되었거나, 노드를 사용할 수 없는 경우 (그러니까, 해당 번호를 사용하기 전에, 다른 번호를 넣어야 하는 경우) continue를 합니다.
그렇지 않다면, 해당 노드를 사용하고 난 다음에 나머지 번호들을 배열하는 가짓수를 결과값에 더합니다. 대략적인 구조는 TSP와 거의 흡사합니다. 다만, check하는 부분이 더 복잡하고, dp식이 다르다는 것만 보일 뿐입니다. 그러면 여러 요소에 대해서는 어떻게 접근하는 것이 좋을까요?
예를 들어 2개의 요소 {1, 3, 4, 7}, {2, 5, 6}이 있다고 생각해 봅시다.

그러면, 노란색 요소가 어떻게 배열이 되어 있는지가, 보라색 요소의 배열 순서의 가짓수에 영향을 미치지 않습니다. 둘은 별개의 시스템으로 돌아가고 있기 때문입니다. 따라서, 보라색을 배열하는 수에, 노란색을 배열하는 수에다가, 보라색으로 칠해진 것들의 자리 4개를 택하기만 하는 가짓수. 이렇게 곱하면 됩니다.
조금 더 생각해 보면, 각 요소를 숫자를 넣지 않고, 그냥 자리만 선택할 때도 곱사건으로 들어갑니다. 그리고 i와 j가 다른 수일 때, i번째 요소의 순서가, j번째 요소의 순서 가짓수에 영향을 주지 않아요. 즉, 요소 안에 원소들이 순서를 잘 선택하는 가짓수 또한 곱사건으로 들어갑니다. 이걸 잘 구현해 주면 되겠네요.
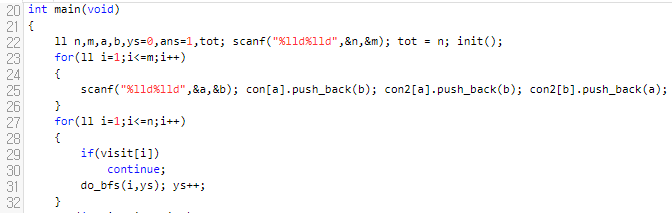
먼저, 방향 그래프와, 방향 없는 그래프 2개를 만듭니다. 그리고, 방향 없는 그래프를 가지고 bfs를 돌립니다. 그러면 해당 요소에 어떠한 간선들이 연결되어 있는지가 나올 거에요. 물론, 이 과정을 con 배열만 가지고 위상 정렬을 해서 돌려도 됩니다만, 저는 그냥 컴포넌트만 추출할 때 방향 없는 그래프도 따로 만드는 편입니다.

calc(i)는 해당 요소에서 순서를 정하는 가짓수입니다. 그리고 C[tot][sz]는 tot개의 자리 중에서, sz개의 자리를 택하는 가짓수입니다. 일단 자리를 먼저 택하고, 요소 안의 순서를 정하면 됩니다. 이 일련의 과정은 독립적으로 작용하기 때문에, 곱사건으로 넣어도 됩니다.
'구현' 카테고리의 다른 글
| 코딩테스트에 나올 만한 백트래킹 쉽게 정복해 봅시다. (0) | 2020.01.28 |
|---|---|
| 백준 16768 : 뿌요뿌요 게임을 구현해 봅시다. (10) | 2020.01.27 |
| 2048 퍼즐 게임 1턴 구현 : 읽는 방향과 flag만 잘 고려하면 어렵지 않아요. (8) | 2019.12.18 |
| 소코반 구현해 보기 : 맵 상태를 쪼개면 답이 보인다. (2) | 2019.12.09 |
| bit 연산 : on/off 상태가 20개 언저리면 고려해 보자 (0) | 2019.11.10 |


최근댓글