백준에서 파이선으로 문제를 몇 개 풀었습니다. 그렇지만 아직 Java나 C만큼 익숙하지 않은 것은 현실입니다. 파이선에는 list.pop(0)이 있는데요. 이것에 대해서 알아보겠습니다.
간단한 테스트 프로그램을 작성해 보겠습니다.

숫자 하나를 테스트 케이스마다 입력 받습니다. 10000000이 nu개 들어있는 리스트가 있는데요. 여기서 맨 앞에 있는 원소를 꺼내 올 겁니다. 이를 9번째 줄의 list.pop(0)이 하고 있습니다.
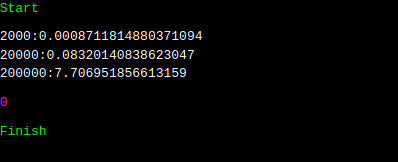
실행 결과는 어떻게 나올까요? 2000, 20000, 20만 이렇게 범위를 늘려가면서 시간을 측정해 보았는데요. 데이터 크기가 10배 늘어날 때 마다, 대략 100배 정도의 시간이 더 걸림을 알 수 있습니다. while 루프는 원소가 빌 때 까지 돌았으니, 총 nu번 돌았을 겁니다. 복잡도가 제곱이 될려면, 루프 안에 있는, list.pop(0)에 의한 것이 nu만큼이였을 건데, 정말 그런지, while loop만 빼고 시간을 측정해 보겠습니다.

이 코드를 실행시켜 보겠습니다.

실행 결과는 위와 같습니다. 완전히 일치하지는 않지만, list.pop(0)은 리스트의 크기가 커지면 커질수록 선형 비례해서 실행 시간이 늘어난다 정도만 보셔도 좋겠습니다. 그러면 이것은 어떤 것 때문에 그런 것일까요? 우리가 배우는 (링크드) 리스트는 앞에 것을 제거하기 위해서, 앞의 것을 찾습니다. 그리고, 그것의 포인터들만 적당히 잘 조정합니다. 그러면 상수 시간만에 수행을 할 수 있습니다. 그런데 그렇지 않다는 것은, 엄청나게 많은 요소들이 0번째 원소를 pop하고 난 후에 어디론가 이동한다는 이야기입니다.

배열이 요래 있었다고 생각하고, 맨 앞에 있었던 3을 삭제해 보겠습니다.

그러면 뒤에 있는 것들을 모두 1칸씩 앞으로 당겨야 합니다. 메모리 카피 함수를 이용하면 상수는 줄겠지만, 배열의 맨 앞을 삭제하는 연산은 복잡도가 배열의 원소 갯수에 비례합니다. 따라서, 맨 앞을 제거하는 연산이 매우 많다면, 파이선의 리스트는 효율적이지 못합니다.
그러면 어떤 것을 써야 할까요?

파이선의 Queue를 가지고 테스트 해 보겠습니다. put은 뒤에 추가를 하고, get은 앞에서 제거합니다.
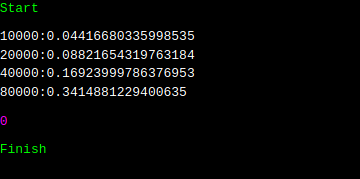
그러면, 일단, 제곱 복잡도에서 선형 복잡도로 낮출 수는 있습니다. 문제는, 너무 상수가 크다는 것입니다. list.pop(0)의 복잡도가 제곱이였지만, 상수가 1/2 정도였다면 이것은 상수가 대략 400 정도나 됩니다. 이게 얼마나 큰 수치인지 감이 안 오신다면, 상수가 생각보다 큰 카라츠바 알고리즘에 대해서 더 찾아보시는 것도 도움이 되실 듯 싶습니다. 상수가 400이 붙었다는 건 더 말할 필요도 없습니다. 100만개가 있었을 때, 대략 4초가 걸린다는 것이기 때문입니다. 그럼에도 n이 20만일 때 7.7초보다는 적게 걸립니다. 저런 식으로 시간이 증가한다면, 20만일 때는 0.34에 3을 곱해도 1.02이니, 7.7보다는 작을 겁니다.

이는 선형보다는 제곱이 더 빠르게 증가하기 때문입니다. 상수보다 이것을 중요시 하는 이유입니다. 복잡도를 낮추는 데에는 성공했습니다. 사실, 이것만으로도 큰 수확입니다. 그런데, 상수가 커서 그런지 썩 만족스럽지는 않습니다. 다른 방법은 없을까요?

파이선의 collections에는 deque가 있습니다. 덱은 앞과 뒤에서 추가, 삭제를 상수 시간에 하게 합니다. nu개를 넣은 것은 똑같았습니다만, 한 가지 다른 것은 queue대신에 콜렉션의 덱을 썼다는 것입니다.
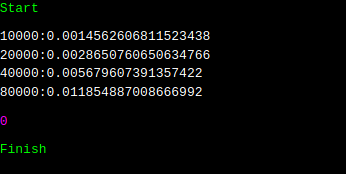
그런데, 실행 시간이 눈에 띄게 빨라졌습니다. 무려 30 ~ 40배. 이는 다른 factor에 의해서, 실행 시간이 극도로 차이가 났다는 이야기입니다. 이것은 이 문서의 마지막 부분에 언급이 되어 있습니다. 그리고 해당 링크에는 lock, locking 등이 상당히 많이 등장하는데요. 이를 토대로 해석해 보면, deque에 비해, queue는 어떠한 이유에 의해서 시간이 매우 많이 걸리는데, 락이 그 이유 중 하나다. 라고 합리적인 추론을 할 수 있습니다.
'레퍼런스 > 분석' 카테고리의 다른 글
| 왜 mutable한 객체를 java map의 키 값으로 삼으면 조심해야 할까요? (0) | 2020.10.09 |
|---|---|
| java toLowerCase toUpperCase 를 수행하면 길이가 항상 같을까요? (4) | 2020.09.27 |
| 언급이 좀 되는 모 자료구조의 보조 해시 함수에 대한 이야기 (0) | 2020.09.02 |
| 해시맵에 있는 tiebreakorder는 어떤 메소드일까요? (0) | 2020.08.28 |
| java ArrayList remove 메소드에 대해 알아봅시다. (0) | 2020.08.25 |


최근댓글