펜윅 트리는 구간합을 구할 때 상수를 줄이기 위해 이용할 수 있는 구조입니다. 유성 문제는 세그먼트 트리 대신에 펜윅을 써야 풀리는 문제로 유명한데요. 시간 복잡도의 특성상 상수를 줄여야 하는데, 레이지를 이용한 세그 트리는 느리기 때문입니다. 이게 어떤 식으로 동작하는지 보고, 간단하게 코드를 작성해 보도록 하겠습니다.
펜윅 트리는 다음과 같이 그릴 수 있습니다.
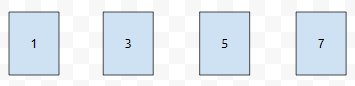
이들은 각각 [1], [3], [5], [7]을 담고 있는 노드입니다. 규칙을 찾아보면, 1, 3, 5, 7은 1의 배수이지만 2의 배수는 아닙니다.

다음에 1, 3, 5, 7과 비교했을 때 구간의 크기가 2배인 2와 6이 있습니다. 이들의 구간 크기는 2이고요. 각각 구간 [1, 2], [5, 6]을 담고 있습니다. 이 둘의 공통점은 2의 배수이지만, 4의 배수가 아니라는 것입니다. 이 특징은 팬윅에서 초기화를 O(nlogn) 대신에 O(n)에 할 수 있게 합니다.

다음에 4는 구간의 크기가 4입니다. [1, 4]를 담고 있다고 할 수 있습니다. 4의 배수이지만 8의 배수는 아닙니다. 이것이 세그 트리에 비해서 얻는 이점은, 공간을 많이 절약할 수 있다는 것에 있습니다. 공간이 2배, 4배, 8배가 커지면, 실행 시간에 어떤 차이가 있나요? 가 궁금하시다면, 제가 백준 사이트에 올린 답글을 참고해 주세요. 그리고 해당 문제에 대한 어느 분의 제출 기록에서 96, 56, 32만 보셔도 어느 정도 감이 잡히실 듯 싶습니다.
그러면, 구간 합 부터 구해보도록 하겠습니다. 구간 [s, e]의 구간합은 구간 [0, e]의 합에서, 구간 [0, s-1]의 합을 뺀 것과 같다는 사실을 이용하면 쉬울 듯 싶습니다. 즉, [4, 5]의 합을 구하기 위해서, [1, 5]의 합과, [1, 3]의 합 2개가 필요합니다. 그러면 [1, 3]의 합을 어떻게 구하면 좋을까요?
[1, 2]와 [3, 3]의 합을 구하면 될 겁니다.
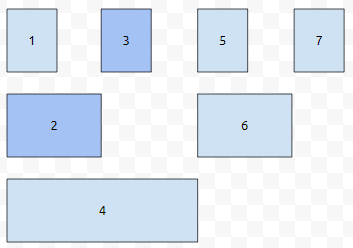
그림으로 보면 2번과 3번 노드에 대한 정보만 가지고 오면 됩니다. 먼저 3을 가져 옵니다. 3은 2진수로 표현하면 11인데요. 2번은 10입니다. 이 둘 사이에 어떤 규칙이 있을까요? 11에서 1이 있는 마지막으로 나오는 1의 자릿수는 01입니다. 11에서 01을 빼면, 10인데요. 이는 2진수로 2임을 알 수 있습니다. 그러면 2번도 가지고 오면 되겠군요.
다음에 10에서, 마지막으로 나오는 1의 자릿수는 10임을 알 수 있어요. 10에서 10을 빼면 0입니다. 끝내면 되겠네요.

다음에 [1, 5] 구간을 봅시다. 5를 2진수로 표현하면 101입니다. 여기서 마지막 1이 있는 자리는 001이라고 할 수 있어요. 5에서 1을 뺀 값은 4인데요. 이를 2진수로 표현하면 100입니다. 101에서 001을 빼면 100으로 일치하는 것을 볼 수 있어요. 다음에 100에서, 1이 나오는 마지막 자릿수는 100임을 알 수 있어요. 100에서 100을 빼면 0이에요.
0은 더할 필요가 없어요. 즉, i에서 (i&-i)를 계속 빼 나가다가, i가 0이 되어 버리면 끝내면 됩니다.

이를 코드로 구현하면 위와 같습니다.
업데이트는 어떻게 하면 될까요? 예를 들어서 위치 3번에 변경이 있었다고 해 봅시다. 배열은 크기가 7입니다.
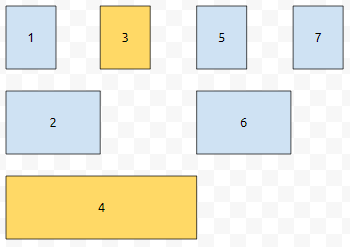
그러면, 노드 3과 4를 업데이트 해야 합니다. 이건 어떻게 나왔을까요? 잘 생각해 보면, 3을 2진수로 표현하면 11입니다. 11에서 마지막 1이 나오는 위치는 01이니까, 11에 01을 더합니다. 그러면, 100이 나오는데요. 이는 2진수로 4를 의미합니다.

한 가지 예를 더 들어보겠습니다. 5를 업데이트 하고자 합니다. 크기가 7인 배열이라면, 5번과 6번을 업데이트 해야 합니다. 5는 자명하고요. 6번이 어떻게 나왔을까요? 5를 2진수로 표현하면 101입니다. 101에서 1이 마지막으로 나타나는 위치는 001이였습니다. 101에 001을 더하면 2진수로 110인데요. 이는 10진수로 6입니다.
즉, (i&-i)를 계속 더해 나가면서, 이 i의 값이 배열의 크기인 n보다 커지면 빠져나오면 됩니다.

이를 코드로 구현하면 위와 같습니다.
이 문제에서는, 배열의 크기가 100만 이하이고, update와 구간 합 계산 쿼리가 많아봐야 2만번 들어옵니다. 그러니, 시간 복잡도는, 초기화 시간 + 구간 합과 업데이트 쿼리에 달려 있을 텐데요.

100만번 update 연산을 수행하였습니다. 초기화를 100만번 update를 한 셈입니다. 이 경우에, 시간 복잡도는 어떻게 될까요? 어렵지 않게 O(nlogn)임을 보일 수 있습니다. 노드 번호가 x인 것이 업데이트 되려면, 어떤 index가 업데이트 되어야 하는가? 에 대한 답을 하면 됩니다.
예를 들어서, x가 4이라고 해 보겠습니다. 그러면, 4번 노드가 업데이트가 되기 위해서, 어떤 인덱스가 업데이트 쿼리에 들어와야 하는가로 바꿀 수 있습니다.

1, 2, 3, 4가 업데이트 해야 하는 index로 들어온다면, 4번 노드가 업데이트가 됨을 알 수 있습니다. 6번 노드가 업데이트 되려면 어떤 인덱스가 들어오면 될까요?

5, 6이 들어오면 됩니다. 이를 일반화 시키면, u가 2^k의 배수이면서 2^(k+1)의 배수가 아닐 때, u번 노드가 업데이트 되게 하는 인덱스의 갯수는 2^k다라는 점을 알 수 있습니다. 이제, 배열의 크기가 (2^k)-1이라고 해 보겠습니다. k는 20이라고 해 봅시다.

그러면 이렇게 그림이 그려질 텐데요. 어려워 보이지만, 하나씩 천천히 해 봅시다. 먼저 2^(k-1), 즉 노드 번호가 2^19의 배수인 노드의 갯수는 하나입니다. 이것을 업데이트 되게 하는 index의 개수는 2^19개입니다. 다음에, 2^(k-2)의 배수이지만, 2^(k-1)의 배수가 아닌 노드의 개수는 2개입니다. 즉, 262144, 786432입니다. 이 노드들이 업데이트 되게 하는 index의 개수는 2^18개입니다. 2에 2^18을 곱하면 2^19입니다.
뭔가가 같은 거 같은 것은 기분 탓일까요? 노드 개수에, 해당 노드가 업데이트 되게 하는 인덱스의 개수를 곱한 값이 같음을 알 수 있어요. 2^(k-1) = 2^19로 말이죠.

이런 게 총 몇 뎁스 있나요? k = 19개 있습니다. 즉, 배열의 크기가 2^k - 1일 때, 노드를 업데이트를 하는 총 횟수는 k*(2^k)입니다. 여기서 2^k = N이라고 하면, k는 log(N)입니다. 따라서, 초기화를 할 때, update 함수를 이용한 경우, 복잡도는 O(Nlog(N))이 됩니다. 이것을 O(N)으로 떨구는 방법이 없을까요?

규칙을 찾아봅시다. 4번 노드는 구간 [1, 4]를, 6번 노드는 구간 [5, 6]을 담당합니다. 4는 2진수로 100, 6은 2진수로 110인데요. 마지막 1의 위치를 가지고 뭔가 하면 될 거 같습니다. 100에서 100을 빼면, 0이고, 110에서 010을 빼면 100입니다. 2진수 0은 10진수로 0, 2진수 100은 10진수로 4를 의미합니다.
즉, i에서 (i&-i)를 뺀 값을 s라고 할 때, nj[i]에서 nj[s]를 빼면, 노드 i번의 총 합이 됩니다.

이렇게 하면 초기화 하는 데 복잡도는 O(n)이 듭니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| java stack 클래스와 대체해서 쓸 만한 arraydeque를 간단히 알아봅시다. (0) | 2023.02.28 |
|---|---|
| heap 자료구조에 build를 어떻게 linear time에 끝낼까요? (2) | 2021.10.13 |
| java map find key in value : 2개의 맵을 씁시다. (0) | 2021.01.28 |
| 스택계산기 구현 : 연산자 우선순위와 결합 순서만 생각해 봅시다. (2) | 2020.07.02 |
| java에서 STL의 multimap 구조를 구현해 봅시다. (2) | 2020.06.24 |


최근댓글