가끔 기하 문제를 다루다 보면, 각도를 알아야 하는 경우가 있습니다. 혹은 주어진 각도를 가지고 무엇인가를 계산하거나. 그걸 하기 위해서는 라디안과 degree를 알아야 해요. 간단하게 알아보도록 하겠습니다.
먼저, python이나 java에서 제공되는 삼각 함수들에 대해 알아봅시다. cos을 예로 들어보겠습니다.

설명을 보시면, Params가 an angle, in radians로 되어 있습니다.
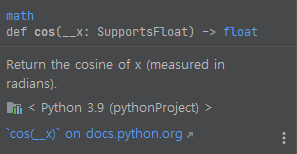
파이썬의 cos도 마찬가지입니다. measured in radians가 들어가 있습니다.
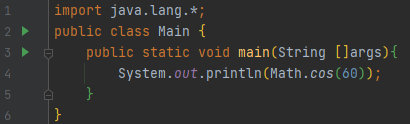
60을 Math.cos의 인자로 넣어봅시다.

그러면, -0.95241298041이 나오는데요. 우리가 알고 있는 cos60도는 0.5인데, 이것과 다른 수치가 나와 버립니다. 이는 Math.cos에 들어가는 것이 degree가 아니라 radian이기 때문이에요.
1라디안은 반지름의 길이가 r인 원이 있을 때, 호의 길이가 r인 것의 중심각 크기에요. 이렇게 말하면 뭔가 어려운 거 같은데요.
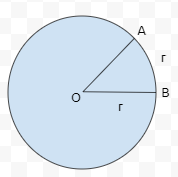
단위 원의 반지름이 r이고, 각 AOB가 1라디안이라면, 호 AB의 길이는 r이 됩니다. 호 AB의 길이가 r*PI인 경우에는 각 AOB가 180도가 될 텐데요. 각 AOB가 1도인 경우에는 호 AB의 길이가 (r/180)*PI가 됩니다. 원의 반지름이 r일 때, 호의 길이가 r이라면, AOB가 1라디안이라 했으니, AOB가 1도인 경우에는 1라디안에 180을 나눈 것에 PI를 곱한 것이 됩니다. 1도를 라디안으로 바꾸기 위해서는, 비례식 x : (r/180)*PI = 1 : r일 때, x의 값을 구한다고 생각하시면 좋겠습니다.
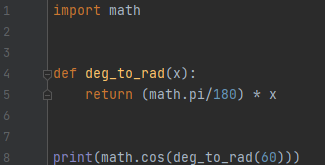
위 프로그램은 각도를 라디안으로 바꿉니다.

예상했던 대로 제대로 나왔네요.
반대로 라디안을 각도로 바꿔야 하는 경우도 있습니다. 이 때에는 반대로 생각하시면 됩니다. 1도가 PI/180라디안이라고 하였습니다. x도일 때 k 라디안입니다. 이 때, k는 알고 있는 값입니다. 이러면 비례식 1 : PI/180 = x : k를 푸는 것과 똑같습니다. k라디안이 몇 도냐를 구하는 문제인데요. 부등식을 잘 풀어 보면, x = (k*180)/PI가 나옴을 알 수 있어요.
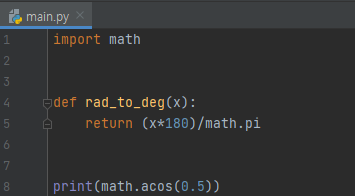
이 내용을 반영한 것은 rad_to_deg 함수입니다. 이제 math.acos(0.5)를 볼게요. acos 함수는 cos 함수의 역함수입니다. 이것의 결과값은 radian 단위입니다.

그러니, 단지 cos(x) = 0.5인 x를 출력하면, 1.0471975511965979가 나옵니다. 어떻게 해야 할까요? 라디안을 degree로 바꿔야 합니다. 구현해 놓은 rad_to_deg를 쓰시면 됩니다.

math.acos(0.5)의 결과를 rad_to_deg의 인풋 값으로 넣고 리턴 값을 받아 봅시다.

그러면 오차는 어느 정도 있지만 약 60도라는 결과를 얻을 수 있습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 정보를 잘 저장해서 사전순 다익스트라 문제를 풀어봅시다. (0) | 2021.08.11 |
|---|---|
| 백준 시철이가 사랑한 수식을 브루트 포스로 검수한 썰 (3) | 2021.05.21 |
| 왜 위상 정렬을 이용하면 그래프 사이클이 있는지 판단할 수 있을까요? (2) | 2021.05.03 |
| 트리 dp : 스크루지 민호 문제로 간단한 것만 풀어 봅시다. (2) | 2021.04.25 |
| 백준 배열 돌리기 5 : 전략적인 브루트 포스로 풀어봅시다. (0) | 2021.04.04 |


최근댓글