그래프에 사이클이 있는지 없는지 판단하는 방법 중 하나는 위상 정렬을 이용하는 것입니다.
어떻게 이용한다는 것일까요?

방향성이 있는 그래프에서, indegree가 0인 게 하나도 없다면 사이클이 있다고 판단합니다. 물론, indegree가 0인 노드가 있는데 사이클이 있는 경우도 있습니다만, 이건 글의 말미에 잠깐 다루겠습니다. 먼저, 아래와 같이 조건을 제한해 보겠습니다. 방향성이 있는 그래프에서 아래 조건이 성립합니다.

이 경우, indegree 값이 0인 노드가 존재하지 않는 그래프에 대해서 판단하는 것 보다는 조금이나마 더 쉽습니다. 사이클이란, i에서 i로 가는 경로를 의미합니다. 제한된 조건을 만족하는 노드 갯수가 n인 그래프를 생각해 봅시다. 일단 indegree 값이 1이므로, 나가는 것이 아니라, 어디서부터 들어오는지에 대해서 생각하는 것이 훨씬 쉽습니다.

먼저, 1번부터 보도록 하겠습니다. 1번은 시작점을 선택할 수 있어요. 1번이 선택한 것이 1이라면 사이클이 생길 겁니다. 1에서 1로 가는 경로 때문입니다. 따라서, 군청색으로 칠해진 노드 중 하나를 1이 선택한다고 보시면 됩니다. 1이 시작점을 선택할 수 있는 가짓수는 n-1입니다.
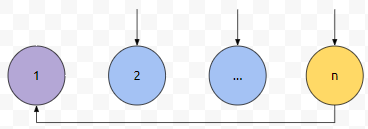
n에서 1로 가는 경로가 만들어 졌습니다. 이제, 2번째 턴입니다. n이 선택해야 하는데요. 선택된 것이 1이라면, 1에서 n에서 1로 가는 사이클이 생깁니다. 선택된 것이 n이라면 n에서 n으로 가는 루프가 생깁니다. 군청색 부분 중에 하나를 택해야 합니다. 이 가짓수는 n-2입니다. n이 2를 택했다고 해 보겠습니다.

그러면, 그림은 위와 같이 그려질 거에요. 이제, 3번째 턴입니다. 2가 종점인 방향이 있는 간선을 선택할 수 있는 가짓수는 n-2가 됩니다. 이런 식으로 턴이 n번째까지 가다 보면 어떤 일이 벌어질까요? 마지막 턴에는, 3이 종점인 간선을 선택해야 한다고 해 보겠습니다.

노란색을 택하자니 3에서 3으로 가는 것 때문에 안 됩니다. 보라색은 어떨까요? 이미 1번이 n을 선택했고, n이 2를 선택했고, ... , ?가 3을 선택한 상황이였습니다. 이 연쇄 과정에서 방문한 것들이 보라색, 노란색으로 표시된 것이였습니다. 이들 중 하나를 다시 재방문 한다? 사이클이 생길 수 밖에 없어요.
따라서, 노드의 갯수가 n이고, indegree가 1인 노드만 있는 경우에는, 사이클이 있습니다.
이걸 조금 더 확장해 봅시다. 방향성이 있는 그래프에서 아래 조건이 성립하면 어떨까요?

이건 어떨까요? 이 경우에는 사이클이 있을까요? 뭔가 어려워 보이는데요.

해당 노드로 들어오는 간선 하나를 빼고 나머지 방향성이 있는 간선들을 점선 처리했습니다. 이것들을 모두 제거해 보겠습니다.

그러면, 임의의 노드의 indegree가 1인 상황과 동일해 짐을 알 수 있어요. 사이클이 있다는 겁니다. 이제, 위상정렬을 이용해서 사이클이 있는지 없는지를 어떻게 탐지하면 될까요? 이 성질을 이용하면 됩니다. 위상정렬을 어떻게 하는지 잘 생각해 봅시다. 각 단계마다, indegree가 0인 노드를 큐에 넣습니다. 큐에서 뺀 노드 from에서부터, to까지 잇는 간선이 있다면, to의 indegree 값을 하나 뺍니다. 하나 빼 버렸는데, to의 indegree가 0이였다. 그러면 큐에 넣는 식으로 위상정렬을 했습니다.
example graph를 보면서 이야기 해 보겠습니다.

처음에 indegree 값이 0인 것은 1이였습니다. 1을 큐에 넣습니다. 다음에 큐에 있는 것은 1 하나이니, 1을 뺍니다. 1을 시작점으로 하는 간선은 1에서부터 2로 가는 것 하나이므로, 2의 indegree 값이 하나 빠집니다.

다음에, 2의 indegree 값이 0이므로, 2가 큐에 들어갑니다. 2 말고는 없으니, 큐에서 빠질 때 2만 빠질 텐데요. 2를 시작점으로 하는 간선은 2에서 3으로 가는 간선과, 2에서 4로 가는 간선 2개이므로, 3의 indegree와 4의 indegree값이 각각 하나씩 감소합니다.

다음에는 어떤가요? 3, 4, 5로 들어오는 간선이 하나가 있어요. 그러므로 위상 정렬이 중단이 되고, 3, 4, 5는 큐에 들어간 기록이 없으므로, example graph는 사이클이 있다고 할 수 있습니다. 즉, 위상정렬을 하는 과정에서, 큐에 들어가지 않은 노드가 있다면 사이클이 있다고 하시면 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 백준 시철이가 사랑한 수식을 브루트 포스로 검수한 썰 (3) | 2021.05.21 |
|---|---|
| 기하 문제를 다룰 때 잘 써먹게 되는 radian degree 변환을 알아봅시다. (2) | 2021.05.16 |
| 트리 dp : 스크루지 민호 문제로 간단한 것만 풀어 봅시다. (2) | 2021.04.25 |
| 백준 배열 돌리기 5 : 전략적인 브루트 포스로 풀어봅시다. (0) | 2021.04.04 |
| 알고리즘 시간 복잡도 대강 분석하는 방법을 예제를 통해 알아봅시다. (0) | 2021.04.03 |


최근댓글