12번째 글은, 냅색 알고리즘 문제입니다. 이것도 꽤 여러 종류가 있는데요. 쪼갤 수 있는 물건이냐, 그렇지 못하냐에 따라서, 그리디로 접근을 할 수 있는지, 아니면 dp로 접근해야 하는지가 나뉩니다. 저는 0/1 냅색 문제를 다뤄 보겠습니다. 이것은 물건을 쪼갤 수 없어요. 물건이 n개가 있습니다. 그리고 가방에 넣을 수 있는 무게는 W입니다. 이 때, 가방에 넣을 수 있는 물건들의 최대 이익은 얼마나 될까요?
먼저 기저 조건을 생각해 봅시다. 물건 0개를 넣었을 때, 가방에 넣은 물건의 총 무게는 0, 이익 또한 0일 겁니다. 따라서, dp[0개][용량 0]을 넣었을 때 값은 0입니다. 대충 이런 경우입니다.

만약에 물건 0개를 넣었는데, 가방에 넣은 물건의 총 무게가 x(x>0)라면 이건 어떨까요? 말이 되지 않아요. 물건 0개를 넣었는데, 가방에 넣은 물건의 총 무게는 x만큼 나가니까요. 모순이 존재합니다. 따라서, 물건 0개를 넣었는데, 넣은 총 무게가 x라면, 당연하게도 -inf로 초기화 해 주어야 합니다. 이는, 가방에 아무것도 넣지 않았는데 무게가 차지하는 경우는 있을 수가 없기 때문에 -inf로 그러한 경우를 제거하는 거에요.
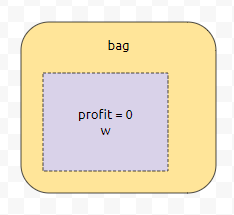
사실 dp[0][x]의 초기값을 0으로 설정해도 크게 문제가 되지는 않습니다. 이 부분은 증명 연습 하실 겸, 증명해 보세요. 기저 조건은 조금만 조심하면 그렇게 어렵지 않아요.
이제, 다음과 같은 dp를 생각해 봅시다.
dp[lo][w]
물건 1부터 lo까지 고려했을 때, 가방에 넣은 물건의 총 무게가 w이다. 이 때 최대 이익
그러면, 우리는 어떻게 하면 될까요? dp[lo][w]를 채우기 위해서, lo번째 물건을 넣는 경우와, 그렇지 않은 경우 둘 다 고려하면 됩니다. 먼저 넣지 않는 경우를 생각해 봅시다.
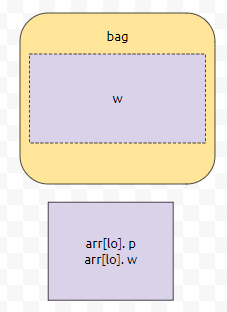
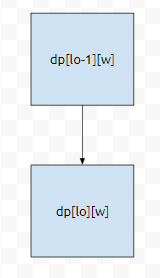
이 경우 dp[lo][w]의 값은 dp[lo-1][w]에서 끌어오면 될 거에요. lo번째 물건을 넣지 않았기 때문에, 이 때에는 물건 1부터 lo-1까지 고려했을 때, 가방에 넣은 물건이 총 무게가 w인 최대 이익만 보면 됩니다. 이걸 다시 그림으로 보면 다음과 같습니다.

이미, 가방 안에 들어간 w만큼의 용량은, 물건을 0번부터 lo-1까지 적절히 넣었을 때, profit의 최댓값을 가지고 있어요. 그렇기 때문에, lo번째 물건을 안 넣은 경우, dp[lo-1][w]를 그대로 빼 와도 됩니다. 문제는, lo번째 물건을 넣은 경우에요. 이 때에는 2가지 경우로 나누면 됩니다. 먼저, w가 lo의 무게보다 작은 경우가 있습니다. 예를 들어서 w가 5입니다. 그런데 lo번째 물건의 무게가 15라고 해 봅시다. 그러면 lo번째 물건을 넣었을 때, 가방에 넣은 무게의 총 합이 5가 되는 경우가 존재할까요?

이미, lo번째 물건을 넣은 시점에서 가방에 넣은 물건 무게의 총 합이 5가 넘어갑니다. 따라서, arr[lo].w가 w보다 큰 경우, lo번째 물건을 넣으면 안 됩니다. 못 넣기 때문입니다. 만약에 그렇지 않다면 어떨까요?
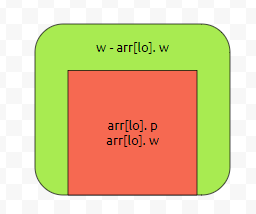
lo번째 넣은 후에, 가방의 총 무게는 w였다고 해 봅시다. 그러면 lo번째 물건을 넣기 전에 가방의 총 무게는 w - arr[lo].w였을 겁니다. 그러면, 우리가 끌어와야 할 값은 dp[lo-1][w - arr[lo].w]입니다. 연두색 부분에 물건 0부터 lo-1까지 잘 넣어서 이익의 최댓값을 만들면 되기 때문입니다.

w - arr[lo].w를 물건 0부터 lo-1까지 채우는 데 최적의 해가 0번, 2번, 3번, lo-1을 택한 거라고 칩시다. 그러면 최적의 이익은 arr[0].p + arr[2].p + arr[3].p + arr[lo-1].p가 될 거에요. 그런데, 단순히 이 값만 끌어오면 될까요? 만약에 그 값만 끌어온다면, 우리는 물건 lo-1까지 넣었고, 이 때 가방에 넣은 무게 총합이 w - arr[lo].w일 때 최대치만 고려한 건데요. 사실 우리는, lo번째 것까지 넣었습니다. 따라서, dp[lo - 1][w - arr[lo].w]의 값에 lo번째 물건을 넣었을 때 얻는 이익인 arr[i].p의 값도 같이 더해야 합니다.
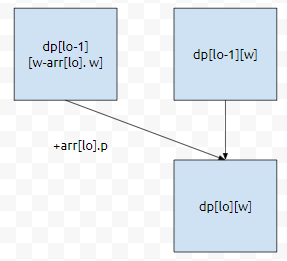
즉, dp[lo][w]를 채울 때, w가 arr[lo].w보다 크거나 같은 경우, 실제로 고려해야 하는 값은 2가지입니다. 하지만 w가 arr[lo].w보다 작다면 lo번째 물건을 넣을 수 없습니다. 그렇기 때문에, lo번째 물건을 넣는 경우를 고려하지 않습니다.
그렇기 때문에, w가 arr[lo].w보다 작은 경우, 고려되는 값은 1가지입니다. 냅색 알고리즘 문제는, 이 부분만 정확하게 이해하고 있다면, 크게 어려운 것이 없습니다.
이제 코드만 간단하게 봅시다. for문이 2중으로 돌고 있는데요.
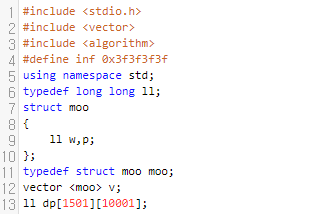
먼저 물건 구조체를 정의했는데요. w와 p는 각각 무게와 이 물건을 가방에 넣었을 때 챙길 수 있는 이익을 의미합니다. 그리고 dp 배열을 잘 보시면, 물건 갯수가 최대 1500개까지 들어오고, 가방의 capacity가 최대 10000까지 들어온다는 것을 알 수 있어요.

이제 초기화를 해 줘야 하는데요. dp[0][0]은 0, x>0이라면, dp[0][x]는 (-1)*inf로 초기화를 해 줍니다. 그리고 1번 물건부터 보기 위해서, 더미 물건을 하나 넣어놓습니다. w가 0이고, profit이 0이다. 라고 정보를 채워 넣으면 좋겠네요. process 함수를 통해서, 물건들에 대한 정보를 넣습니다.

그리고, 26번째 for loop는 제가 위에서 주구장창 설명했던 내용들을 그대로 코드로 옮겨놓은 것입니다. i가 arr[i].w보다 작은 경우와, 그렇지 않은 경우로 나눠서 안쪽 for문을 돌고 있음을 알 수 있어요. 이는 내가 가방 안에 넣은 총 무게가 w인데, arr[i].w보다 w의 값이 작다면 i번째 물건을 넣을 수 없기 때문에 그런 것입니다.
그런데 답을 구할 때, 여러 가지 경우를 보는데 이건 왜 그런 걸까요? 용량이 3이고, profit이 2인 경우, 용량이 3이고 이익이 3인 경우, 그리고 가방에 넣을 수 있는 무게가 100인 경우, 답은 5가 되어야 할 겁니다. 2개의 물건을 다 넣을 수 있기 때문입니다. 그런데 dp 배열에 어떤 식으로 들어갔는지 보면 다음과 같이 나옵니다.
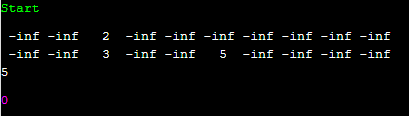
이는 우리가 dp[lo][w]를 0번부터 lo번 까지의 물건들을 적절히 선택해서 가방에 정확히 w만큼의 무게를 넣었을 때 이익의 최댓값으로 정의했기 때문입니다. lo까지 보았을 때, 가방에 들어간 총 무게가 0인 경우, 1인 경우, ... , w인 경우를 모두 고려해야 하는 이유입니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| stable sort : 우선 순위가 같은 데이터들은 어떻게 정렬될까요? (4) | 2019.07.14 |
|---|---|
| 삽입 정렬 알고리즘 : 원소가 들어갈 위치는 어디인가? (2) | 2019.07.11 |
| 대우 명제 : 언제 이 도구를 증명하기 위해 쓸까요? (0) | 2019.07.06 |
| dfs 심화편 : 깊이 우선 탐색의 단점을 어떻게 보완하는가? (0) | 2019.06.28 |
| 외판원 문제 : 팩토리얼을 지수 복잡도로 낮춰보자 (8) | 2019.06.27 |


최근댓글