bfs는 뎁스가 깊어질수록 생성되는 state 수가 매우 많아집니다. 그러면, depth를 줄일 수만 있다면, 속도가 획기적으로 개선된다는 이야기 또한 됩니다. 시작점과 도착점에서 동시에 bfs를 하는 방식을 양방향 bfs라고 하는데요. 이렇게 하면, s에서 e로 가는 최적해가 2x일 때, s에서 x만큼, e에서 x만큼의 깊이만 탐색하면 됩니다. s에서만 출발하면 2x만큼 탐색하는 것에 비하면 거의 절반 가까이 줄어버린 셈입니다.
일단 어떤 식으로 탐색을 하는지 개략적으로 보고, 입문 문제를 풀어보도록 합시다. 백준에서 흔히 알려진, 루빅의 사각형은 구현이 안 되면 매우 힘든 문제이기 때문에, 입문 문제로 제외하였습니다.

branch factor가 b라고 해 봅시다. 즉, 한 상태를 queue에서 뺐을 때, 인접한 상태가 최대 b가 나온다고 한다면, depth가 1일 때에는 1 + b개를 탐색하면 될 겁니다.

그런데 depth가 2일 때에는 최대 1 + b + b^2개를 탐색해야 할 거에요. 잘 보시면 t(1)도 최대 b개의 상태가 걸려 있고, t(2) 또한 b개의 상태가 걸려 있어요. 그러니까 depth가 2인 노드의 갯수는 최대 b^2개가 나오겠네요.
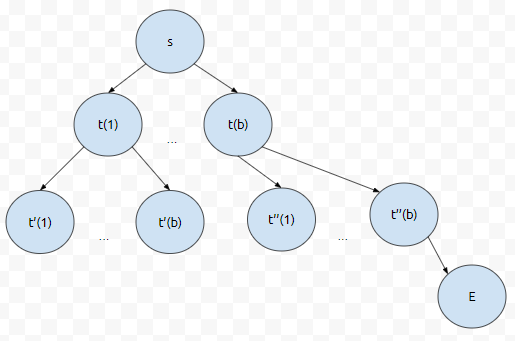
그러면 실제로 S에서 E상태로 가는 최적 해가 3인 경우에, 최대 몇 개의 노드를 봐야 하나요? 1+b+b^2+b^3개를 보아야 합니다. 만약에 b = 700 ~ 800이라면 꽤 클 겁니다. 최적 해가 4인 경우에는 또 어떤가요? 700^4는 49만의 제곱과 같은데요. 이 값은 2500억 가량 됩니다.
그런데, 사실 반씩 쪼개서 본다면, 뎁스가 2일 때까지만 탐색하면 된다는 것을 알 수 있어요. 그러면 실제로 보는 상태 수가 50만 가량으로 매우 많이 줄어든다는 것 또한 알 수 있습니다. 이는 추후에 배우실 Meet in the middle 에서도 같은 아이디어가 적용됩니다. 그러면 대략적으로 어떻게 탐색하면 될까요? s에서 돌리고 e에서 돌리라고 했으니까, 두 포인트에서 동시에 BFS를 돌리시면 됩니다.

저는 s에서 먼저 확장시키고, e에서 확장시키겠습니다. s에서 E까지 최적 해가 3이라면, 루트 s에서 뎁스 1만큼 탐색하고, 루트 e에서 뎁스 1만큼 탐색하면 이 둘이 만나지는 않을 거에요. 다음에 어떻게 하면 좋을까요?
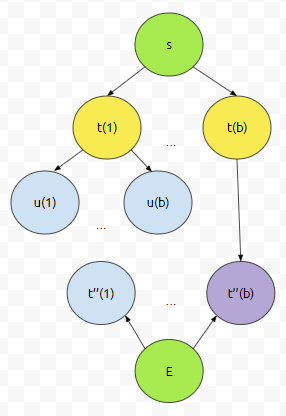
일단 s에서 expand를 시킵시다. 즉, 노드 t(1), ..., t(b)가 expand가 될 거에요. 그러면 이걸 어떻게 할 거냐면, E에서부터 출발했을 때 만난 상태들과 만나는지 생각해 봅시다. 쭉 보다가, t(b)와 인접한 상태 t''(b)가 E에서부터 출발했을 때 만난 상태들입니다.
따라서, 이 때 최적해는 3이 됩니다. s에서 t(b)까지 거리는 1, t(b)에서 t''(b)까지 거리는 1이였고, E에서 t''(b)까지 거리 또한 1이였기 때문입니다. 요약하면, 시작점과 도착점에서 동시에 bfs를 돌리면서, 어딘가에서 확장한 상태에 방문한다면, break를 걸기 때문에, 뎁스가 거의 절반으로 줄어버린다. 라는 겁니다.
입문 문제로 백준에 있는 1229번 문제를 보도록 하겠습니다. 루빅보다 쉬우면서, 양방향 탐색에 대해서 물어볼 만한 것은 다 물어보고 있기 때문에 선정하였습니다. 먼저, 수열 s = {1, 6, 15, 28, 45, 66, ... } 이렇게 있습니다. 계차 수열인데요. 이 s에 속한 수들 k개의 합이 n입니다. 예를 들어서 n이 5라면 1+1+1+1+1로 나타낼 수 있으니까, s 안에 있는 수 5개로 나타낼 수 있습니다.
n이 10^6보다 작거나 같은 자연수일 때, k의 최솟값을 구하라는 게 문제입니다. 친절하게도 답이 5인 가장 큰 n은 130이라고 주어져 있습니다.
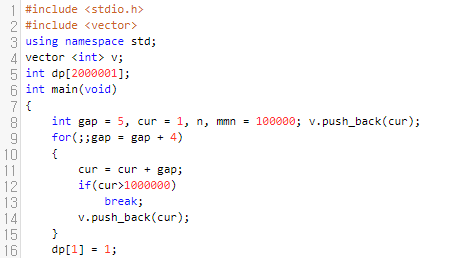
그러면 먼저, 수열 s에 속한 수들을 벡터 v에 모두 저장을 해 놓습니다.
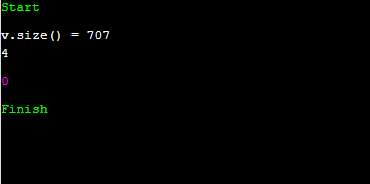
그런데, 100만보다 작으면서 s에 속해있는 수들은 707개입니다. 흔히 아는 냅색 비스무리한 dp로 풀어버리면 100만에 707을 곱한 게 단위 연산일 텐데요. 7.07억이면 1초 안에 돌지 모르겠습니다. 그렇다고, 130 이상인 수에 대해서 bfs를 깡으로 돌리자니, 707^4의 값이 2494억입니다. 배보다 배꼽이 더 크겠군요. 실제로는 더 빨리 돌겠지만, 그래도 10억이 넘어갈 가능성 매우 높습니다.
그러면 일단 n = 130까지는 일반적인 dp 채우는 방법으로 채워 봅시다. dp[x]를, x를 s 안에 있는 수, 최소한 몇 개로 채워야 하는가로 정의해 봅시다.

보시면, dp[x]를 구하기 위해서, j는 0부터, v[j]가 i보다 작거나 같을 때 까지 돌면서 dp[i-v[j]] + 1의 최솟값을 갱신해 주고 있어요. 예를 들어서 10을 만드는 가짓수는, 마지막에 1을 넣는 경우와, 6을 넣는 경우가 있기 때문에, dp[9] + 1의 값과, dp[4] + 6. 이 두 값의 최솟값으로 갱신해 주는 것입니다.
그런데 n>130인 경우, 답이 아무리 커도 4보다 크지 않다는 것을 알고 있습니다.

그러면, 4의 절반인, depth = 2까지만 보면 된다는 소리입니다. branch factor가 707인데요. 뎁스가 2인 경우, 봐야 하는 상태는 s에서 출발할 때 707^2개, e에서 출발할 때 707^2개니까, 대략 100만개 정도만 보면 됩니다. 그러면 이걸 어떻게 양방향 탐색을 적용시켜야 하나요? 일반적인 bfs와는 다른 거 같은데 말입니다.

간단합니다. 우리는 어짜피, 수 k가 주어지면 s안에 있는 수들을 최소한 몇 개 써야 만들 수 있느냐를 구하면 됩니다. 물론 중복 허용하고요. 그러면 k = a + b꼴로 나타낼 수 있을 건데요. 답이 4 이하라면, dp[a]의 값이 2 이하이고, dp[b]의 값이 2 이하인 a와 b가 존재합니다.
그러면, 우리는 이런 아이디어를 생각해 볼 수 있습니다. 130까지는 dp값을 채우고, 131부터는 v 안에 있는 수들을 보면서 채워나가면 되지 않을까?

보시면 dp[v[i]]의 값은 1입니다. v는, 수열 s에 포함된 수이기 때문입니다. 예를 들어 1, 6, 15와 같은 수들입니다. 이들은 각각 1, 6, 15 하나의 합으로만 만들 수 있어요. 다음에 34번째줄부터 41번째 줄까지를 보면, dp[v[i] + v[j]]의 값을 갱신해 주고 있는데요. 이는 최대 2입니다. 이들도 같이 갱신해 줍니다.

다음에 우리는 i + (n-i) = n이기 때문에 dp[i]와 dp[n-i]의 합을 가지고 오면 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 퀵 정렬 평균 시간 복잡도 : 왜 O(nlogn)일까? (4) | 2019.08.20 |
|---|---|
| k번째 수 찾기 : count sort를 응용해 봅시다. (2) | 2019.08.17 |
| 퀵 정렬 : bad partition이 발생할 경우 문제가 된다. (4) | 2019.08.15 |
| 슬립 정렬 : 아이디어는 좋은 거 같은데.. (8) | 2019.08.13 |
| 비교 기반 정렬 : 왜 하한이 nlogn일까? (2) | 2019.08.10 |


최근댓글