백준 11004번, k번째 수를 구하는 문제가 있습니다. 오름 차순으로 정렬하였을 때, k번째 수가 무엇인지를 묻는 문제입니다. 그런데 배열의 크기가 500만입니다. 그렇기 때문에 fast io를 쓴 다음에 sort를 쓰거나, 아니면 다른 방법을 써야 하는데요.
저번에 배운 count sort를 조금 응용해 보도록 하겠습니다.
[관련 글]
이게 k번째 수와 어떠한 관련이 있을까요? [0, 20억] 사이에 있는 수는 다음과 같이 표현할 수 있습니다.
65536a + b (단 a, b는 0보다 크거나 같고 65536보다 작은 자연수)
즉, 65536 진법으로 표현할 수 있습니다. 그러면 몫을 구할 때 (x>>16)을, 나머지를 구할 때에는 (x&65535)로 구할 수 있어요. 그러면 배열에 있는 500만개의 수들은, <a, b> 쌍으로 표현할 수 있을 겁니다. 단, a는 arr[i]를 65536으로 나눈 몫, b는 나머지를 의미합니다.

대충 이런 식으로 배열이 있다고 해 봅시다. 우리는 이 중, 4번째 수를 구해볼 거에요. 그러면 우리는 먼저 몫을 기준으로 count 해야 할 겁니다. 왜냐하면, 65536 진법 시스템에서, 몫이 1이지만 나머지가 0인 수가 몫이 0이지만 나머지가 65535인 것보다는 크기 때문입니다. 그렇기 때문에 먼저 pair 중에서 a 값을 기준으로 먼저 count 하는 겁니다.
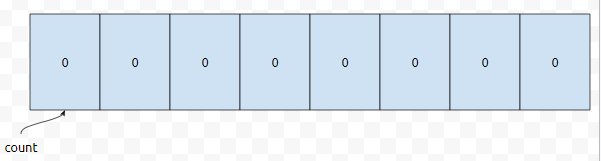
처음에 count는 다음과 같이 초기화 되어 있습니다. 들어올 수 있는 값의 범위가 [0, 65535]이니까 65536개만큼만 할당하면 된다는 것에 주목하세요. 먼저 <2,4>가 들어옵니다. 앞에 있는 값이 2이므로 co[2]의 값이 하나 증가합니다.
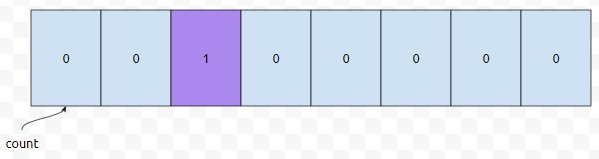
다음에 들어오는 데이터는 <1,7>입니다. 첫 번째 값이 1이므로, co[1]의 값이 증가합니다.
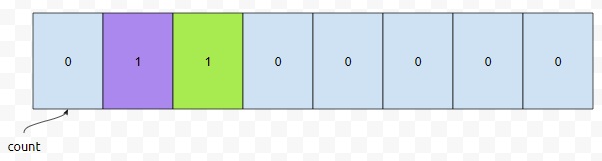
다음에는 <6,3>이 들어옵니다. pair의 첫 번째 값이 6이기 때문에, co[6]이 하나 증가합니다.
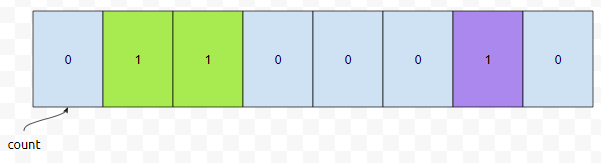
다음에 <2,2>, <5,1>, <0,6>이 들어옵니다. 그러면 co[2], co[5], co[0]의 값이 각각 1씩 증가합니다.

최종적으로 채워진 count 배열은 다음과 같습니다. 이제, 누적 배열을 정의할 건데요. nj[x] = 어떠한 값이 [0,x] 범위를 가지는 총 갯수? 정도로 정의하시면 어떤가요? 예를 들어서 nj[3]은, pair가 <a,b>꼴로 주어진다고 하였을 때, 앞에 있는 값이 0, 1, 2, 3인 것의 갯수 정도로 생각하시면 좋을 듯 싶군요.

그러면 일단, nj[0]의 값은 co[0]입니다. nj[1]이 문제인데요. 이것은 nj[0]에다가 co[1]을 더하면 됩니다. 따라서, 누적 카운트 배열에서 co[1]의 값은 1에 1을 더한 2가 됩니다.
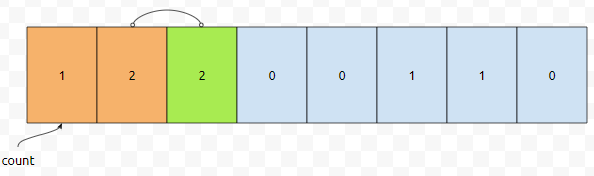
누적 카운트[2]는 어떻게 구할까요? 이미 우리는 nj[1]의 값인 2를 알고 있습니다. 그러면 nj[1]에다가 co[2]를 더하면 될 겁니다. 2에다가 2를 더하면 4가 됩니다. 따라서 누적 카운트[2]의 값은 4가 됩니다.
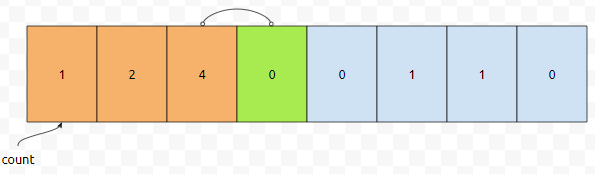
알고리즘을 대충 보면 아시겠지만, 누적[3]을 구하기 위해서, 누적[2]와 co[3]의 값을 계속 보고 있음을 알 수 있어요. 이런 식으로 계속 채워나가다 보면, 실제로 채워지는 정보값은 아래와 같을 겁니다.
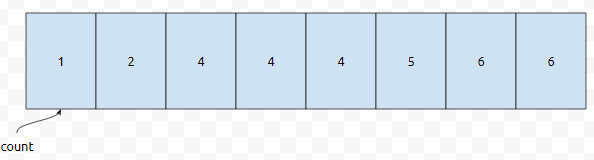
여기서, count[2]는 a의 값이 0, 1, 2인 pair의 갯수입니다. count[3]은 a의 값이 0, 1, 2, 3인 pair의 갯수이고요.
이제 이 정보를 가지고 크기순으로 정렬했을 때, 4번째 pair의 a 값을 구해야 합니다.

그러면 이것은, 누적값 x-1가 4보다 작지만, x가 4보다 크거나 같은 최초의 시점을 찾으면 됩니다. pair 중에서 a의 값이 0, 1인 것의 총 갯수는 2개이지만, 0, 1, 2인 것의 갯수는 4개입니다. 그리고 4는 4보다 크거나 같습니다. 따라서, 4번째 pair의 a값은 2임을 알 수 있어요.
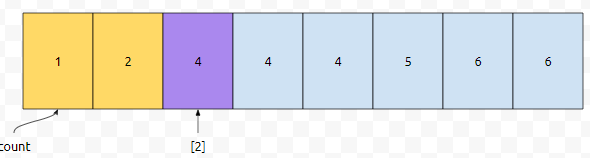
그러면 4번째로 작은 원소를 구하기 위해서는 어떻게 해야 할까요? 일단 a의 값이 0과 1인 것의 갯수는 2였습니다. 그러면, a의 값이 2인 것 중에서 크기 순으로 2번째인 것을 구하면 된다는 것을 알 수 있어요.
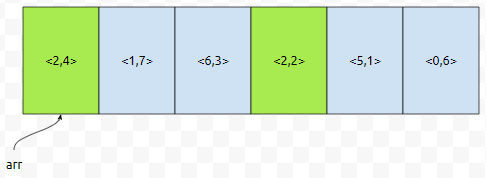
a의 값이 2인 것만 count 시킵니다. count를 할 때, b의 값을 넣습니다. 즉 <2,4>를 넣을 때는 co[4]가 하나 증가하고, <2,2>를 넣을 때는 co[2]가 하나 증가하는 식입니다.
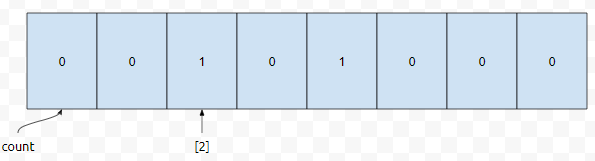
그러면 카운트 배열에 다음과 같이 들어갈 겁니다.
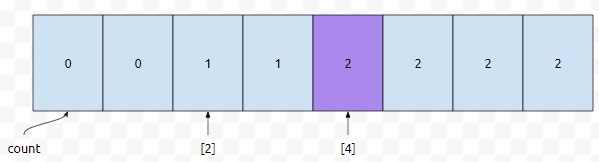
그리고 누적 배열은 다음과 같이 채워질 겁니다. 여기서 2번째로 작은 pair를 구해야 합니다. a의 값이 2이면서 b의 값이 0, 1, 2, 3인 pair의 갯수는 1개입니다. 그런데, a의 값이 2이면서 b의 값이 0, 1, 2, 3, 4인 것의 갯수는 2개입니다. 1은 2보다 작고, 2는 2보다 크거나 같기 때문에, b값은 4임을 알 수 있어요.
따라서, 크기 순으로 정렬하였을 때, 4번째 페어는 <2,4>입니다. 저는 크기가 n인 배열을 2번 돌았습니다. 그리고 추가 공간은 65536개만큼 잡았습니다. 나오는 값의 범위가 [0, 65535]이기 때문입니다. 따라서, O(2n)의 복잡도를 가집니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 왜 유클리드 알고리즘 함수는 최악의 경우 O(log)일까? (2) | 2019.08.21 |
|---|---|
| 퀵 정렬 평균 시간 복잡도 : 왜 O(nlogn)일까? (4) | 2019.08.20 |
| 양방향 탐색 : 시작점과 도착점에서 동시에 탐색을 한다. (5) | 2019.08.16 |
| 퀵 정렬 : bad partition이 발생할 경우 문제가 된다. (4) | 2019.08.15 |
| 슬립 정렬 : 아이디어는 좋은 거 같은데.. (8) | 2019.08.13 |


최근댓글