5002번째로 푼 문제는 이 문제였습니다.
문제 상황을 간단하게 요약하면 아래와 같습니다.

1순위가 같으면 2순위를 처리하는 것은 나중에 생각해 보도록 합시다. 우리가 원하는 것은 '탑승 비용', 문제에서 설명하는 route cost를 최소화 하는 방법부터 고민해 보겠습니다.
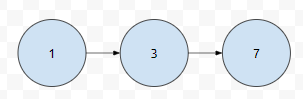
비행기 1이 도시1에서 3을 거쳐서 목적지인 7로 간다고 해 봅시다. 대충 1에서 7로 가는데 3을 경유한다고 보시면 됩니다. 이 경로를 선택하는 비용이 10이라고 해 보겠습니다. 문제에서 설명하는 것에 따르면 1에서 3으로 가는 탑승 비용, 3에서 7로 가는 탑승 비용, 1에서 7로 가는 탑승 비용이 10으로 같습니다. 이 세 경우는 경로 1을 선택해서 갈 수 있는 경우이기 때문입니다.
문제는, 비용 10을 어느 간선에 줄 것이냐는 것입니다.

1과 3으로 가는 경로에 주면 될까요? 그러면 3에서 7로 가는 경우를 고려하지 못합니다.
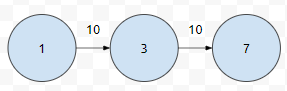
이 경우는 어떤가요? 1에서 7로 가는 경우 잘못 계산이 될 겁니다. 좋은 방법이 없을까요?
이런 관점에서 생각해 봅시다. 노선 1번을 비행기 1번이 운행한다고 해 보겠습니다. 지역 1에 있는데 비행기 1 안에 있는 경우, 지역 1에 있는데 비행기 1 바깥에 있는 경우가 있을 겁니다. 이걸 간단하게 나타내 보면 아래와 같습니다.
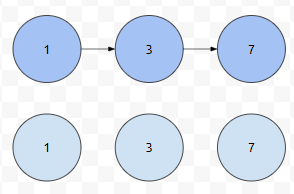
여기서 군청색은 지역 1에 있으면서 비행기 1에 탑승한 경우를, 하늘색은 비행기는 탑승하지 않았는데 지역 1에 있는 경우를 의미합니다. 1에서 3을 경유해서 7로 가는 경로를 가는 주체는 비행기입니다. 비행기를 타지 않으면, 1에서 3으로, 혹은 3에서 7로, 혹은 1에서 7로 갈 수 없습니다.
즉, 비행기를 탑승했다면, 그 순간에 경로를 선택한 비용, route cost를 청구하면 됩니다.

거꾸로, 군청색 i에서 하늘색 i로 가는 비용은 어떻게 구하면 될까요? 이를 우리는 지역 i에 도착했을 때 비행기에서 '내리는 행동'으로 표현할 수 있습니다. 이미 하늘색에서 군청색으로 들어왔을 때, 경로를 선택한 비용이 청구 되었으므로, 군청색에서 하늘색으로 갈 때는 따로 청구할 필요가 없습니다.
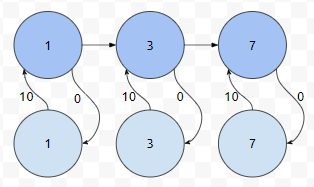
이제, 우리는 노선 1이 있을 때, 1번에서 7번으로 이동하는 경로를 이렇게 구할 수 있습니다. 하늘색 1에서 하늘색 7로 가는 비용. 10임을 알 수 있습니다. 1이 비행기 1 안에서의 1과, 비행기 바깥에서의 1로 분할 되었음을 알 수 있습니다. 이를 정점 분할이라고 합니다. 정점에 비용이 적혀져 있을 때에는 어떻게 하면 될까요?
간단합니다. 정점에 막 들어온 상태와, 정점을 통과해서 막 빠져나온 상태 둘로 분리하면 됩니다. 예를 들어서, 정점 7의 비용이 10이라고 하면, 아래와 같이 모델링을 할 수 있습니다.

7in에서 7out으로 가는 데 10만큼의 비용이 든다. 이제 7에서 9로 가는 비용 3짜리 간선을 추가해 보겠습니다.

7out에서 9in으로 이어지는 간선의 가중치가 3인 것을 보시면 됩니다. 이 트릭은 다익스트라 뿐만이 아니라 플로우에서도 꽤 자주 보이는 트릭이니 익혀두시면 좋습니다. 정점 분할해서 이분 매칭을 하더라. 플로우를 돌리더라. 대충 이런 의미라고 생각하시면 됩니다. 자세한 언급은 하지 않겠습니다.
3에서 2로 이어지는 노선을 선택하는 비용이 2라고 해 보겠습니다. 이 노선을 추가해 보겠습니다.
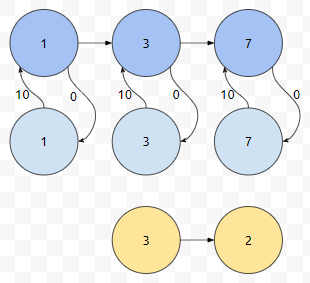
그러면 그림이 이렇게 그려질 겁니다. 파란 노선과 노란색 노선. 노란색 노선을 택한 경우에도 비용이 청구되는 것을 간과하시면 안됩니다. 2, 3번 지역에서, 노란색 노선을 탈 수 있다면, 아래와 같이 연결하시면 됩니다.
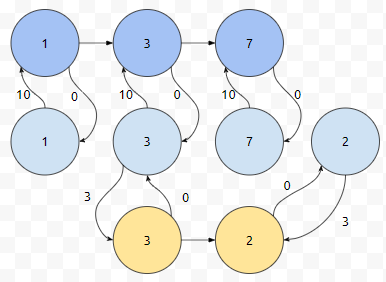
비행기2 안에서의 3과, 바깥에서의 3, 그리고 비행기2 안에서의 2와 바깥에서의 2 이렇게 분할되었음을 알 수 있습니다. 1에서 2로 가는 최소 비용은 어떻게 구하면 될까요? 파란색 노선을 택한 비용 10에, 노란색 노선을 택한 3 요렇게 구하시면 됩니다. 노선 n개에 대해서도 마찬가지로 작업해 주시면 노드가 최악의 경우에 대략 10만 1000개 정도니, 100만은 넘지 않습니다.
문제는 2차 기준도 최소화를 해야 한다는 것입니다.

이것은 간단하게, 비행기를 타고 i번 공항에 착륙했을 때, 방문 횟수가 1 증가했다고 해 보겠습니다. 내리지는 않았습니다. 내가 탄 비행기가 어떤 지역에 방문했을 때 비용 1이 추가된다고 보시면 됩니다. 즉, 빨간 간선에 +1을 set 해야 합니다. 문제는, 1차 기준인 하늘색에서 군청색으로 가는 경로가 빨간 간선의 값보다는 훨씬 중요하다는 것입니다. 좋은 아이디어가 없을까요? 검은 간선의 비용에다가 적당히 큰 수 M을 곱하면 어떨까요? 예를 들자면 131072 같은 것이요.
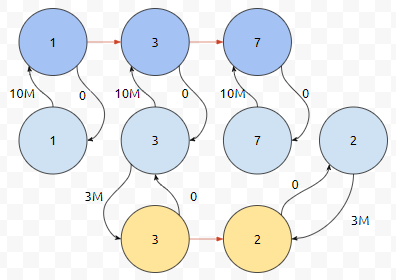
우리는 노선에서 빨간 간선을 최대 몇 번 지나느냐를 볼 필요가 있는데요. 도시 번호는 1보다 크거나 같고, 1000보다 작거나 같다고 되어 있습니다. 빨간 간선을 1000번 이상 갈 수 있을까요? 여기서 빨간 간선이라는 것은 비행기를 탄 상태에서 i에서 j로 이동했다는 의미입니다.
이동 과정에서, 같은 장소를 다시 방문할 필요가 없습니다. 왜냐하면, 같은 장소를 방문할 바에야, 그 장소에서 안 움직이는 것이 낫기 때문입니다.
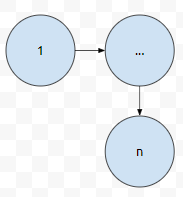
같은 장소를 2번 이상 방문하지 않는다면 최악의 경우에 a에서 b까지 이동하는데, 빨간 간선을 n-1번 쓸 겁니다. 중요한 건 n-1은 커 봤자 999라는 것입니다. 따라서 M을 적당히 큰 수인 131072로 두고 모델링을 하면, 복잡한 1차, 2차 기준 처리할 필요 없이 간단하게 처리할 수 있습니다.
이렇게 하였을 때, A에서 B까지 최단 거리는 long long 범위 내에 들어올 수 있는지는 증명해 보도록 합시다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| functional graph 에서 사이클을 어떻게 묶어낼까요? (0) | 2021.01.26 |
|---|---|
| 많이 언급되는 오프라인 쿼리 간단하게 훑어봅시다. (0) | 2021.01.04 |
| 수학적 귀납법을 활용하여 문제를 풀어봅시다. (0) | 2020.12.24 |
| 백준 1060번 구간 : 후보해를 추린다. (0) | 2020.12.03 |
| 백준 소수인팰린드롬 : 팰린드롬인지 먼저 검사한다. (0) | 2020.11.12 |


최근댓글