안녕하세요. 그래프 이론에서 functional graph는 생각보다 많이 다뤄지는 주제입니다. 이 사이트를 보셔도 좋을 듯 싶군요. 울프람 알파에도 정의가 되어 있습니다. 이 그래프에서 어떻게 사이클을 찾을까요? 예전에, scc (강한 연결 요소)를 모르던 시절에 풀었던 문제들이 몇 개 있었습니다. 그 문제들을 풀 때 써먹을 수 있는 흥미로운 것들은 2개 입니다.

여기서 노드 i와 노드 j가 같은 덩어리에 속해있다면 i에서 j로 갈 수 있는 방법이 있거나, j에서 i로 갈 수 있는 방법이 있다는 것을 의미합니다. 이 둘을 보이도록 하겠습니다.
상대적으로 보이기 쉬운 2번부터 보여봅시다. 그래프에서 cycle은 시작점 s가 있다고 해 봅시다. 여기서 출발해서 다른 노드들을 거쳐서, s로 도착하는 경로가 있다면, 이 경로를 cycle이라고 이야기 합니다. 예를 들어서, 1번에서 출발했는데, 2, 4, 5를 거쳐서 1로 돌아오면 1, 2, 4, 5, 1은 사이클 경로입니다.
그러면, 이 때 사이클에 속하는 노드는 들어오는 간선과 나가는 간선이 최소 하나 이상 있을 겁니다.
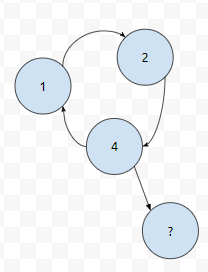
만약에, 사이클 s에 속한 원소에서 s에 속하지 않는 원소로 나가는 간선이 있다고 해 봅시다. 위 그림에서는 4는 사이클 s에 속하는 1로 연결이 되어 있고, s에 속하지 않는 ?에 연결이 되어 있습니다. 2개에 연결이 되어 있는데요. functional graph는, x와 인접한 원소가 하나입니다. 즉, outdegree가 하나입니다. 그런데 4의 outdegree는 둘입니다.
이 생각을 발전을 시켜 봅시다.
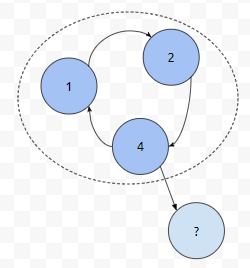
사이클 요소에서 다른 노드로 연결될 수 있을까요? 그럴 수는 없다는 것을 알 수 있습니다. 이미 사이클 내에 있는, 군청색 노드들은 outdegree가 1 이상인 상황입니다. 그런데, 사이클에서 다른 노드로 연결되면, 사이클 내의 최소한 한 요소는 outdegree가 1보다 커지는 상황이 발생해 버립니다.
따라서, 사이클 요소에서 다른 곳으로 나가지 않습니다. 이제 1번을 보여 봅시다. 그런데, 이것도 사실 복잡한 문제는 아닙니다.
노드 i와 노드 j가 한 덩어리에 속해있다는 것은, i에서 j로 가는 방법이 있거나, j에서 i로 가는 방법이 있다는 것입니다.
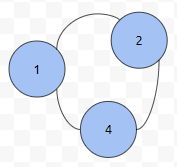
1번과 2번과 4번이 연결되어 있습니다. 그런가요?
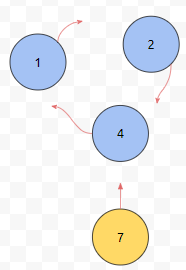
나가는 간선으로만 봅시다. 어떠한 노드에 들어오는 간선의 수는 제한이 없지만, 나가는 간선의 수는 단 1개이기 때문입니다. 그러면, 덩어리 내에 노드가 n개가 있다면, 노드 하나 당 나가는 간선의 수가 1개씩 있으니, 총 간선의 수도 n개가 될 겁니다.
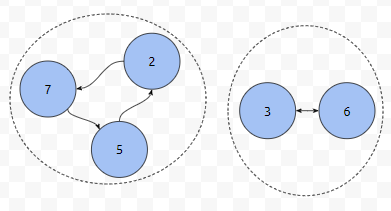
사이클이 2개가 있고, 1번 사이클에 노드 a개, 2번 사이클에 노드 b개가 있다고 하면, 덩어리 두 개에 대해서, 간선 갯수는 a+b개일 겁니다. 다음에, 이 둘에 속하지 않는 것들 c개도 한 덩어리에 연결이 되어야 한다고 해 봅시다.
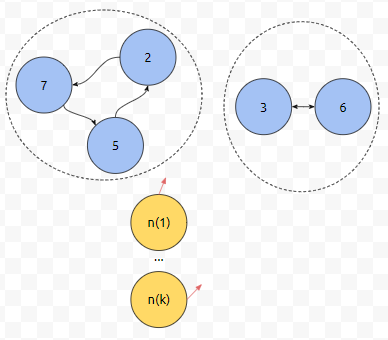
k개의 Vertex는, k개의 Edge를 가지고 있습니다. 이 부분은 부정하지 못할 겁니다. 문제는, 무리 1과 무리 2도 n(1), ... , n(k)와 같은 덩어리에 속하기 위해서 필요한 최소 간선의 수는 k+1개라는 점입니다. 만약에 저 무리들까지 한 덩어리에 속했다면, Vertex 수는 k+a+b개가 될 거고, Edge 수는 (k+1) + a + b가 됩니다.
그런데 중요한 것은 노드 하나당, out degree 수는 하나이므로, 노드 수가 k+a+b개라면, edge도 당연하게도 k+a+b개가 되어야 합니다. 사이클이 2개 이상 연결되면, 모순적인 상황이 발생해 버립니다. 따라서, 컴포넌트 하나당 cycle은 많아야 하나입니다. 그러면, 적어도 사이클은 몇 개가 될까요?
많아봐야 사이클은 하나이고, cycle 내에서는 루프로만 가는 경로만 있으므로, 아래와 같이 도식화를 시킬 수 있습니다.

물론, 사이클이 없는 경우도 있다고 생각하실 수도 있습니다.
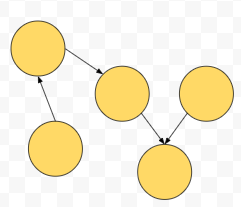
대충 이런 경우입니다. 그런데, 이 경우에는 말단 노드가 있습니다. 이것은 out degree가 0입니다. functional graph가 아닙니다. 아앗. 그렇군요. 따라서 사이클은 최소 하나 존재할 겁니다.
이제 백준 6523번 문제를 보겠습니다. 문제는 기니까 생략을 하고, 중요한 조건만 찾아 보겠습니다.

(2)번 조건이 까다로울 수 있습니다. 그런데 잘 생각해 보면, x에서 f(x)로 가는 건 dfs로 생각할 수 있습니다. 그리고 우리는 dfs던 bfs던, 이미 방문한 상태를 다시 방문하지 않습니다. 2번 이상 걸리기 위한 단계 수가 10^6보다 작다는 이야기는, 10^6번의 단계 전에, 이미 걸렸던 사람이 다시 걸렸다는 의미입니다. 방문한 데를 다시 방문했다는 의미입니다.
dfs나 bfs에서의 상태가 이 문제에서는 사람으로 페러프레이징이 된 셈입니다. toeic에서 제가 RC를 못 푸는 이유일까요?

따라서, 사이클 길이만 잘 구해 주면 됩니다. 말을 돌려서 표현한 것 뿐입니다.

소스 코드는 위와 같습니다. 단지, 우리는 visit를 map으로 선언해 놓고 관리하면 됩니다. 이미 방문한 지점을 다시 방문하였을 때, 몇 번째로 방문했는지를 저장해 놓는다면 사이클의 요소도 구할 수 있고, 길이도 구할 수 있습니다. 최초로 다시 방문한 지점이 k라면, k부터 쭉 돌면서 다시 k가 나올 때 까지 순회하면 되기 때문입니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 여러 트릭에 응용되는 트리에서의 dfs ordering을 알아봅시다. (0) | 2021.03.07 |
|---|---|
| 백준 최소 환승 경로 : 허브와 노드를 생각하자. (0) | 2021.02.07 |
| 많이 언급되는 오프라인 쿼리 간단하게 훑어봅시다. (0) | 2021.01.04 |
| 정점 분할 : 노드를 상태에 따라 여러 개로 쪼갠다. (2) | 2020.12.29 |
| 수학적 귀납법을 활용하여 문제를 풀어봅시다. (0) | 2020.12.24 |


최근댓글