재귀 함수를 배우셨으니까, 제일 유명한 문제 중 하나인 하노이탑 알고리즘을 구현해 봐야 겠어요. 보통 하노이의 탑 문제는 기둥이 3개이고, 작은 기둥 위에 큰 기둥이 올 수 없다는 조건이 걸려있는 문제를 말해요. 또 한 번에 하나의 원판을 옮길 수 있는데요. 물론 백준에는, 기둥이 4개이 문제도 보입니다. 그건 논외로 합시다. 99xx번대에 있던 걸로 기억하는데 말입니다. 이걸 어떻게 구현하면 좋을까요? 생각보다 난이도가 조금 있어 보이는데요. 답은 재귀에 있습니다. 이 부분에 대한 내용은 관련 글에 충분히 설명이 되어 있으니, 개념 이해가 아직 안 되셨다면 보시고 오시는 게 좋아 보입니다.
[관련글]
먼저 기저 조건을 봅시다.

옮길 원판의 갯수가 0개이면 어떤가요? 어떠한 연산도 수행할 필요가 없습니다. 따라서 이 경우, 재귀 호출을 하지 않고 그냥 바로 리턴해 버리면 됩니다. 그러면, 1개의 원판이 있을 때, 그것을 1에서 3으로 옮기는 연산은 어떻게 수행이 될까요?

먼저 원판 1을 1에서 3으로 옮기기 위해서, 0개의 원판을 3과 1이 아닌 다른 위치로 옮겨야 하는데요. 1 위에 아무것도 없기 때문에, 이러한 과정들은 생략이 됩니다.
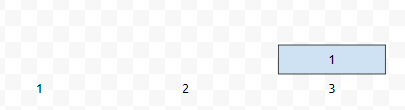
막바로 원판 1이 1에서 3으로 옮겨집니다. 그리고, 0개의 판이 2에서 다시 3으로 옮겨질 텐데요. 역시 2에 있는 판은 아무것도 없기 때문에 이 과정은 생략됩니다. 그냥 n이 1일 때, 1이 from에서 to로 갔다고 출력해도 될 듯 싶네요. 어짜피 원판이 1개라면, 그것 위에 있는 판은 아무것도 없기 때문에, 바로 해당 판이 출발지점에서 목적 지점으로 갈 수 있거든요.
이제 n개를 옮기는 경우를 생각해 볼게요.
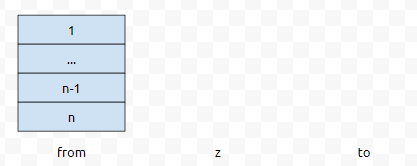
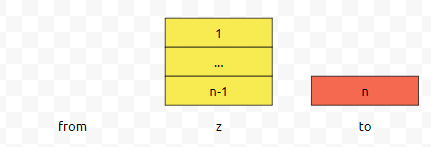
저는 n개의 판을 from에서 to로 옮기는 게 목적입니다. 어떻게 하면 좋을까요? 확실한 것은 n 위에 있는 n-1개의 판을 어딘가로 옮겨야, n을 옮길 수 있다는 겁니다. 일단, 1부터 n-1까지를 한 덩어리로 보고, n을 한 덩어리로 봅시다.

그러면 이 노란색 덩어리를 from에서 어딘가로 옮겨야 할 건데요. to로 옮기면 어떤가요?
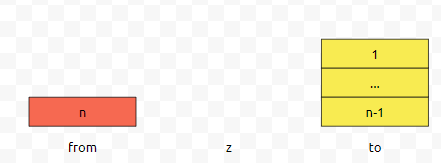
n이 to로 갈 수 없어요. 따라서, 노란색 덩어리는 from에서 z로 옮겨야 합니다.
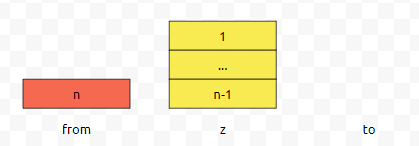
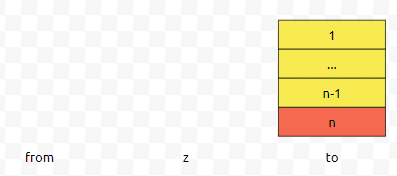
그 다음에 n번째로 큰 원판을 from에서 to로 옮깁니다.
그리고 노란 덩어리를 z에서 to로 옮기면 됩니다.
그러면, 우리는 n개의 원판을 옮기기 위해서, 노란색 덩어리를 옮길 공간인 z가 필요함을 알 수 있어요. 이를 노란색이 경유할 경유지라고 해 봅시다. 즉, 우리는 hanoi 변수를 4개 받으면 됩니다. n개의 덩어리가 출발할 번호, 노란색 덩어리가 빨간색 판을 위해서 잠시 대기할 경유지, 도착할 번호, 옮길 원판 갯수. 이렇게요.
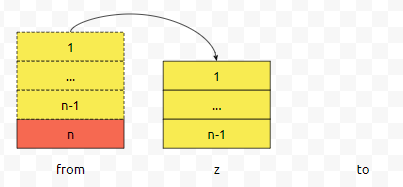
그러면 노란색 덩어리들은 from에서 z로 옮겨야 할 건데, 이건 어떻게 해야 하나요? n-1번 원판을 from에서 z로 옮기기 위해서는 1부터 n-2까지의 원판들이 from에서 to로 옮겨져야 합니다.
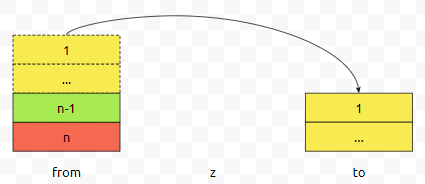
그리고 n-1번 원판을 z로 옮기면 되겠죠. 이 때 n-1개의 원판에서 맨 밑에 것을 제외한 나머지 녀석들은 to를 경유지로 삼은 것입니다. 즉, hanoi(from,to,z,n-1); 을 호출하면 될 거에요.

노란색은 to에 있다가 다시 z로 가면 되거든요. 그 다음에는 어떨까요?
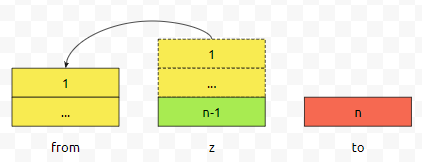
n-1개의 덩어리를 z에서 to로 옮기기 위해서는, 노란색으로 칠한 부분을 z에서 from으로 옮겨야 합니다. 그래야, 초록색으로 칠한 것을 z에서 to로 옮길 수 있기 때문입니다.
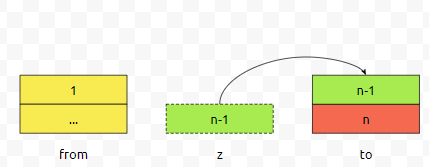
그 다음에 연두색 부분을 z에서 to로 옮긴 다음에, 노란색을 from에서 to로 옮기면 되겠습니다. 즉, n을 from에서 to로 옮긴 다음에 n-1개를 z에서 to로 옮길 때, 중간 경유지는 from이 되는 셈입니다.
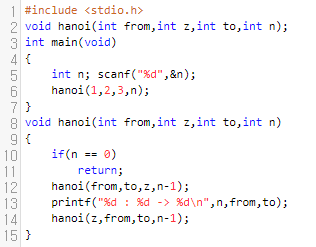
제가 말한 내용을 코드로 구현하면 위와 같습니다. 먼저 n개를 from에서, 경유지 z를 거쳐서 to로 가게 했습니다. 이 중에서 n번째 원판은 바로 from에서 to로 가고, 나머지는 z를 반드시 거쳐가게 되어 있어요. 그러면 n-1개의 원판은 먼저, from에서 z까지 갔다가, 다시 z에서 to로 가야 합니다. 이것은 각각 12, 14번째 줄에 설명이 되어 있어요.
그런데 원판이 3개라면, 2개를 from, to로 쓴다고 하면, 나머지 하나는 경유지가 될 거에요. 그렇기 때문에, 12번째 줄에서는 hanoi(from,to,z,n-1)을, 14번째 줄에서는 hanoi(z,from,to,n-1)을 호출한 것입니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| 올바른 괄호 문자열 검사하기 : 스택으로 손쉽게 해결해 보자. (2) | 2019.07.20 |
|---|---|
| 자료구조 스택 : 먼저 넣은 것이 나중에 빠진다. (12) | 2019.07.18 |
| 재귀 함수 : 자기 자신을 호출한다. (2) | 2019.07.08 |
| 링크드 리스트 : 왜 순회 시간이 배열보다 오래 걸릴까요? (4) | 2019.07.04 |
| 동적 배열 : expand 연산을 이해하는 것이 핵심이다. (0) | 2019.06.23 |


최근댓글