스택을 응용한 문제 중에는, 히스토그램에서 가장 큰 직사각형이라는 문제가 있습니다. 히스토그램 안에서 그릴 수 있는 직사각형 중, 넓이가 가장 큰 직사각형의 넓이를 구하는 문제입니다. 이것은 푸는 방법이 상당히 많습니다. 세그먼트 트리로 풀어도 되고, 분할 정복으로 풀어도 됩니다. 여기에서는 우리가 배운 스택을 응용해서 풀어보도록 하겠습니다.
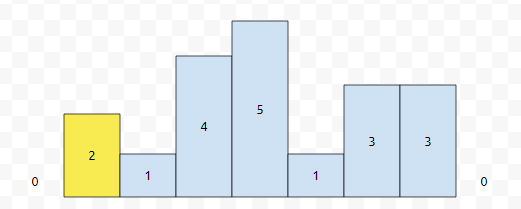
먼저 데이터가 다음과 같이 들어왔다고 해 봅시다.

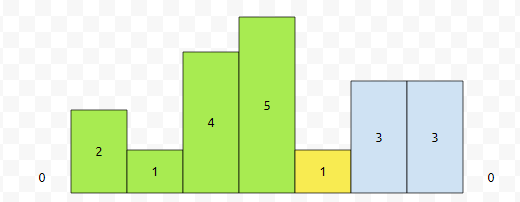
히스토그램에서, 총 7개의 직사각형이 있어요. 그러면 arr[0]과 arr[8]은 0으로 초기화를 합니다. 이를 더미 데이터라고 합니다. 처리하기 쉽게 처리한 겁니다. 그리고 arr[1] = 2, arr[2] = 1, arr[3] = 4, arr[4] = 5, arr[5] = 1, arr[6] = arr[7] = 3이라는 값이 들어가 있어요.
여기서 어떻게 가장 큰 직사각형을 찾을까요? 스택을 이용하면 됩니다. 먼저 왼쪽에서 오른쪽 방향으로 훑어봅시다.

먼저 0번째 직사각형의 높이는 0이다. 라는 정보를 넣습니다.
다음에, 우리는 1번째 직사각형의 h가 2이다라는 정보를 넣어야 하는데요. 스택의 top에 있는 높이 값이 0입니다. 이 값보다, 현재 보고 있는 직사각형의 높이 값이 더 크거나 같으므로, 그대로 stack에 push 합니다.
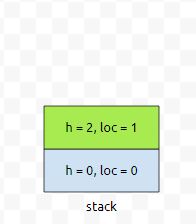
그 다음에 2번째 사각형을 볼 겁니다.

제가 노란색으로 칠한 부분을 볼 건데요. 이 상태에서, stack의 top에 있는 원소를 어느 정보를 담고 있나요?
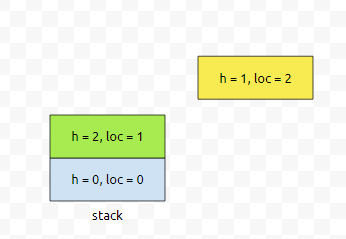
location 1에 있는 친구의 높이는 2다. 라는 정보를 가지고 있어요. 이 값은 제가 넣을려는 높이 정보보다 큽니다. 따라서, 초록색 부분을 pop 합니다. 그리고 나서, 어떤 정보를 저장할 거냐면요.
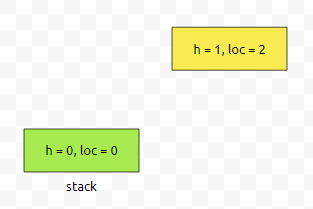
loc = 1에서의 information은 loc = 2라는 정보가 들어왔을 때 stack에서 pop 되었다는 것만 저장할 거에요. 어렵지 않죠? 즉, ri[1]의 값에 2를 넣을 겁니다. 이것이 무엇을 의미하는지는 천천히 시뮬레이션 하면서 보여드리도록 하겠습니다. 그러면 스택의 맨 위에 있는 원소는 h = 0이라는 정보를 가지고 있는데요. 이것은 제가 넣을려는 정보인 h = 1보다 작거나 같습니다. 따라서, 그대로 push를 하면 됩니다.

어렵지 않아요. 다음에 어떻게 하면 좋을까요? 오른쪽을 봐야 할 거에요.

그런데, 오른쪽은 높이가 4에요. 위에 있는 정보는 height가 1이다. 입니다. 스택의 맨 위에 있는 정보보다는, 제가 보고 있는 직사각형의 높이가 더 크거나 같아요. 그렇기 때문에, 그냥 push 하면 됩니다.

이제 4번째 사각형을 넣어 봅시다. height가 5입니다.
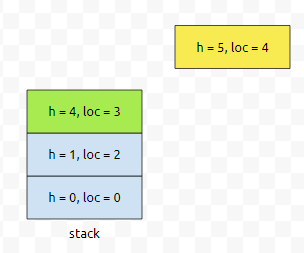
이는, 스택의 맨 위에 있는 높이보다 크거나 같으므로, 그냥 push 하면 됩니다.
이제, 5번째를 넣어 볼 건데요. 높이가 1이에요.
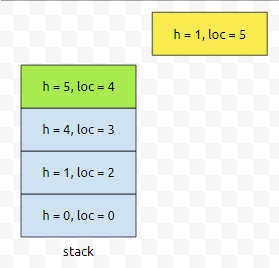
그러면, 스택에서 어느 친구들이 pop 되어야 할까요? 높이가 1보다 큰 것들이요. 이것을 보라색으로 표현해 봅시다.

이 부분이 빠져야 할 것들입니다. 이것들을 히스토 그램상에서 표현해 봅시다.

보라색으로 칠한 이 둘이 5번째 rectangle이 들어올 때 빠집니다. 이 5라는 값은 무엇을 의미할까요? 보라색으로 칠한 4는, 3번째 직사각형을 의미합니다. 구간 [3,3]의 최솟값은 4입니다. 구간 [3,4]의 최솟값 또한 4입니다. 하지만, 구간 [3,5]의 최솟값은 4가 아닌 1입니다.
즉, ri[x]는 구간 [x,k]에서 최솟값이 arr[x]가 아닌, x보다 큰, 최초의 k를 의미합니다. 그러면 ri[4]의 값 또한 5입니다. 이것은, 우리가 스택을 통해서 쉽게 알 수 있는데요. 어떠한 새로운 정보, lo'번째의 height는 hh'이다 라는 것이 들어왔을 때, stack에서 lo번째 사각형의 높이가 hh다라는 정보가 빠진다는 것은, lo번째 information을 넣을 때 부터, 새로운 정보가 들어오기 전까지는 hh보다 크거나 같은 정보들만 들어왔다는 겁니다. 즉, [lo, lo'-1]의 최솟값은 hh이지만, [lo, lo']의 최솟값은 hh' 이다라는 소리가 됩니다.

이제 6번째와 7번째에 대한 정보를 넣겠습니다. 둘 다 높이가 3이에요.
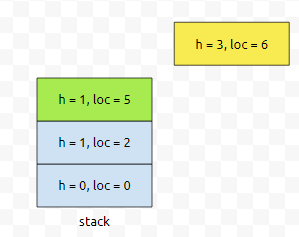
그렇기 때문에, 둘 다 스택의 top에 있는 height와 비교해도 작지 않아요. 그렇기 때문에 계속 push가 될 거에요.

그리고 8번째 높이는 0입니다. 그러면 보라색 부분이 빠질 거에요.

ri[2], ri[5], ri[6], ri[7]에 8이라는 정보를 넣습니다.

ri 배열을 채운 결과는 다음과 같습니다. 천천히 스택을 그리시면서 시뮬레이션을 해 보시면 이해가 가시리라 생각합니다. 그러면 [k, x]의 최솟값이 arr[x]가 아닌 최대 k는 어떻게 구하면 좋을까요? 역방향으로 돌리시면 됩니다.

먼저 8번째의 높이가 0이다라는 정보를 비어 있는 스택에 push 합시다.
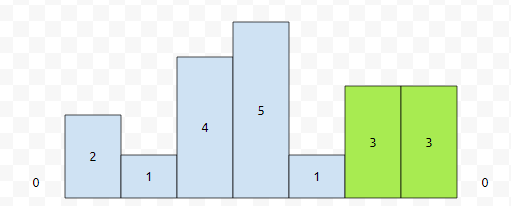
다음에, 두 연두색으로 칠한 것을 차례대로 push 합시다. 우측부터 좌측으로 보는 것이니까 0, 3, 3 이렇게 변하면 계속 push가 일어날 거에요.
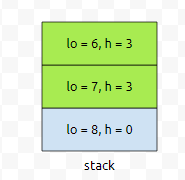
그러면, 스택에 요런 식으로 들어갈 거고, 그 다음에 5번째 높이가 1이다. 라는 정보가 들어옵니다.
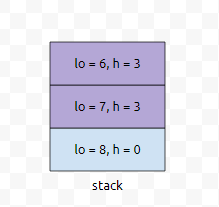
그러면, 보라색 부분이 빠집니다. h 값이 들어갈 정보인 1보다 크기 때문입니다. 즉, le[6]과 le[7]의 값은 5로 업데이트 되는데요. 이것은 구간 [6,6]의 최솟값이 arr[6]이고, 구간 [6,7]의 최솟값이 arr[7]이지만, 구간 [5,6]의 최솟값과 구간 [5,7]의 최솟값이 각각 arr[6]과 arr[7]이 아니라는 소리입니다. 뭔가 방향만 다른 거 같은데, 방향만 다를 뿐, 스택에 정보를 넣고 빼고 하는 알고리즘은 똑같습니다. 왼쪽과 오른쪽은 방향만 반대인 관계라는 것을 간파하셨다면요.

이 그림을 보시면 조금 더 명확하리라 생각합니다. 요런 식으로, arr[0]까지 쭉 돌면, le 배열은 이렇게 채워집니다.
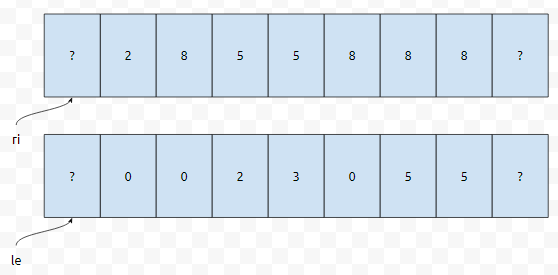
이제 이 배열을 가지고 어떻게 처리할 건지 생각해 봅시다.

노란색 부분을 봅시다. 높이가 4에요. 3번째에 있고요. le[3]의 값은 2였습니다. 그 이야기는 구간 [2,3]의 최솟값은 4가 아니지만, 구간 [3,3]의 최솟값은 4라는 소리에요. 왼쪽으로는 3까지밖에 갈 수 없다는 의미입니다. 그런데 ri[3]의 값은 5였습니다. 이 이야기는 구간 [3,5]의 최솟값은 4가 아니지만 구간 [3,4]의 최솟값은 4라는 소리입니다. 즉, 우측으로는 4까지 확장이 가능합니다.

노란색 부분을 보세요. ri[3]과 le[3]의 차이는 3입니다. 구간 [3, 4]에 있는 정수의 갯수는 2입니다. ri[i] - le[i] - 1의 값을 w[i]라고 해 봅시다. 그리고, arr[i]의 값을 h[i]라 했을 때, w[i]에 h[i]를 곱한 값이 후보해가 될 수 있다는 겁니다. 이 후보해들 중, 최댓값을 출력하면 됩니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| 이중 연결 리스트 : 노드를 연결하는 포인터가 2개다. (0) | 2019.07.27 |
|---|---|
| 자기 참조 구조체 : 간단하게 이해해 봅시다. (2) | 2019.07.24 |
| 올바른 괄호 문자열 검사하기 : 스택으로 손쉽게 해결해 보자. (2) | 2019.07.20 |
| 자료구조 스택 : 먼저 넣은 것이 나중에 빠진다. (12) | 2019.07.18 |
| 하노이탑 알고리즘 : 재귀 호출의 대표적인 문제를 구현해 봅시다. (5) | 2019.07.12 |


최근댓글