retainAll이라는 메소드의 시간 복잡도에 대해서 질문이 들어왔습니다. AbstractCollection에 있는 메소드인데요. 결론부터 말씀드리겠습니다. 간단하게 정리하면, 인자로 넘어가는 Collection의 contains에 따라서 갈리게 됩니다. 그런데, retainAll이 따로 재정의된 케이스도 있기 때문에 시간 복잡도를 분석하실 때 주의가 필요합니다. 밑에서 후술하겠습니다.
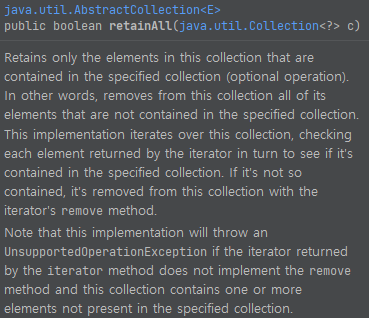
먼저 이 메서드의 설명을 봅시다. Collection에서 retainAll을 호출할 때 이 메서드를 볼 일이 적지 않기 때문입니다. c에 있는 원소들만을 획득한다. 라고 설명이 되어 있네요. 그리고, UnsupportedOperation 예외를 떨굴 수도 있다고 하는데요. 삭제 연산을 지원하지 않는다면 떨어트려지게 됩니다. 예제 몇 개를 보면서 시간 복잡도를 분석해 봅시다.

먼저, hs1에서 has1에 있는 원소들만을 취하게끔 하는 예제입니다. hs1은 HashSet, has1은 ArrayList로 되어 있어요.

retainAll 메소드를 보면, 현재 iteration이 가리키고 있는 원소가 c에 없으면 그 원소를 remove 해 버리게 되는데요. contains 메소드 안으로 들어가 봅시다.

ArrayList의 contains는 indexOf를 호출합니다.
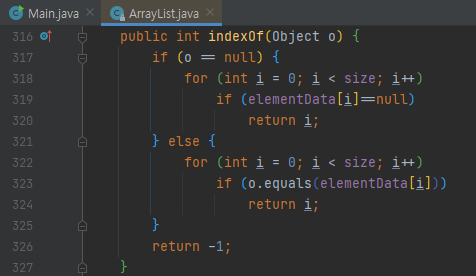
이 메서드를 보면, 최악의 경우 size만큼 돈다는 것을 알 수 있는데요. size는 ArrayList의 크기입니다. has1의 크기가 n이라면 최악의 경우에, contains 메소드는 O(n)만큼의 비교를 해야 할 겁니다. 다음에 iteration의 remove인데요. A.retainAll(B)에서 A에 걸리는 이터레이터를 의미합니다.

디버그 흐름을 계속 따라가다 보면, Hashiterator의 remove를 보게 되는데요. 조금 더 들어가 보겠습니다.

결국, HashMap의 removeNode를 호출합니다. 충돌이 많이 일어나는 경우에도 꽤 빠르게 동작합니다.

그림으로 그리면 이런 것인데요. A가 hashSet이였고 B가 ArrayList였습니다. ArrayList의 contains가 오래 걸릴 뿐, HashSet에서 다음 원소로 가는 연산이나, HashSet에서 현재 원소를 remove 하는 연산은 순식간에 동작합니다. 따라서, A의 원소 갯수가 a, B의 원소 갯수가 b라 하면 최악의 경우에 O(ab)에 동작합니다.
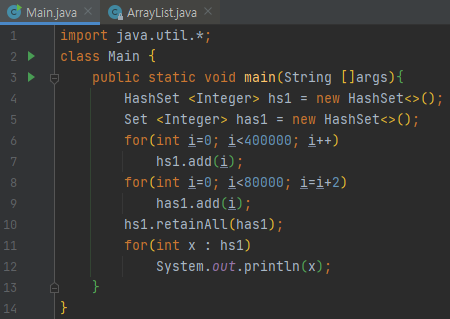
이 경우는 어떨까요? hs1과 has1이 hashSet이였습니다.

그러면 HashSet에서의 contains 메서드와 현재 원소의 다음 값을 찾는 연산, 그리고 현재 원소를 제거하는 연산 등의 비용을 따져야 하는데요. 뒤에 있는 두 연산은 상수에 작동합니다. 앞에 contains가 문제인데요. hashSet은 내부적으로 hashMap을 들고 있어요. 그래서, 내부적으로는 hashMap의 containsKey를 봐야 하는데요.

키의 해시값을 가지고 버킷에서 값을 찾아나가게 됩니다.

그래서, comparable 하다면, 최악의 경우에 O(alogb)의 복잡도를 가지게 됩니다. 생각보다 빠르게 동작한다는 것이 중요합니다.
이 경우에는 어떨까요? 빠르게 동작할까요? 위에서 보았던 abstractList의 retainAll이 호출되면 매우 느릴 것은 자명합니다.
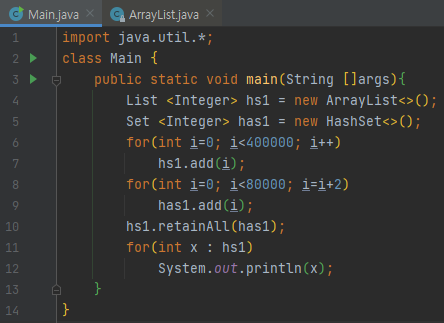
그런데 실행 시켜 보면 생각보다 훨씬 빠르게 동작함을 알 수 있어요. 제가 위에서 보여드렸던 retainAll 메소드를 실행시키면 엄청 오래 걸릴 텐데 그렇지 않습니다. 왜? 내부를 보면 단번에 알 수 있습니다.
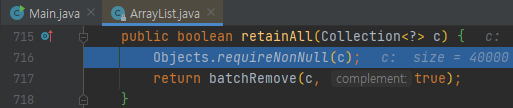
ArrayList는 abstractList를 상속받습니다. 그래서 일단 이 메서드가 불릴 겁니다. 중요한 것은 batchRemove인데요.

원소가 포함되어있는지를 검사하고 있다면, elementData에 임시로 반영시킨 다음에 arrayCopy 메서드를 이용해서 한꺼번에 반영시켜버립니다. A.retainAll(B) 이런 식으로 호출했고 A가 ArrayList라면, B의 contains 복잡도에 따라서 retainAll의 복잡도가 달라진다는 의미입니다.
'레퍼런스 > 분석' 카테고리의 다른 글
| java number 클래스에 대해 간단하게 알아봅시다. (0) | 2022.03.07 |
|---|---|
| java 9 부터 도입된 Map.of 메소드를 알아봅시다. (0) | 2022.02.28 |
| python dictionary는 최악의 경우에 정말로 시간 복잡도가 선형일까요? (0) | 2021.11.06 |
| 여러 필드가 있을 때 해시값을 리턴하는 java objects의 hash 메서드를 알아봅시다. (0) | 2021.08.21 |
| java list removeall vs clear : 언제 쓰는지 정확하게 알아봅시다. (0) | 2021.08.09 |


최근댓글