python에서 dictionary가 어떻게 구현되었을까요? 아니 그 전에 최악의 경우에 뭔가를 찾는 연산은 O(n)일까요? insert 하는 연산도? 사실, 저는 자바에서 본 것 처럼 그냥 chaining 으로 관리하지 않을까 싶었는데 그건 아니였습니다. 니다. 제 무지함이 또. 그 전에, 정말 최악의 경우에 insert나 find 연산 등이 비효율적으로 동작할까? 에 대한 의문부터 해결해 봅시다.
최악의 경우를 인위적으로 만드는 방법은 그리 어렵지 않습니다. 어디까지나 인위적으로 조작할 뿐, 실제로 제가 출제한 문제에서 최악 케이스를 만드는 건 쉽지 않습니다. 왜냐하면, python에서 int object가 모든 hashcode 값이 0일 리는 없기 때문입니다. 이에 대한 건 나중에 언급하도록 하겠습니다. 이 글에서는 그냥 임의의 객체를 하나 만들고 충돌을 매우 많이 일으킬 수 있게 셋팅해 보겠습니다.

Obj 클래스에 field x가 있어요. 여기서 __eq__와 __hash__를 재정의 하는데요. java로 치면 equals와 hashcode를 의미해요. 이 값이 어떠한 Obj 객체이던 0이 나오게 한다는 의미는 모든 Obj key에 대해서 충돌을 일으키겠다는 의미입니다. dict가 오픈 어드레싱을 쓴다고 합시다. 그리고 키 값이 해당 위치에 이미 있을 때에는 우측으로 1칸 이동한다 해 봅시다. 아래와 같은 그림이 그려질 거에요.

처음에 해시 값에 버킷 수를 나눈 나머지를 구해 봅시다. 예를 들어 hash 값이 0이라면 0에 버킷 수를 나눈 나머지는 0이니까 0번 인덱스에 접근해 볼 겁니다. 그런데, 비어 있습니다. 그대로 넣습니다.

그러면 0번 위치에 0이 들어간 상태에요. 다음에 hash 값이 0인 객체 3이 들어왔다 해 봅시다. 그러면 먼저 해시 값에다가 버킷 갯수를 나눈 나머지가 0이니까 0번 인덱스부터 볼 겁니다. 그런데 0번은 이미 가득 차 있어요. 그 다음에 몇 번 버킷을 봐야 할까요? 저는 그냥 간단하게 1만큼 이동하겠습니다.
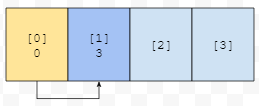
다음에 해시 값이 0인 객체 2를 추가해 봅시다. 그러면 0번 부터 보게 될 텐데요. 0번 인덱스는 이미 있으니까, 그 다음에 1번으로 이동해 보는데요. 1번에도 있네요? 그러니, 2번으로 이동하는데요. 2번에는 없어요.

대충 어떤 그림인지 감이 오시나요? 해당 위치에 충돌이 발생했을 때, 다음 위치를 어디로 잡을 것인지 탐사를 하고 있어요. 물론, dict는 이것보다는 훨씬 복잡한 방법을 쓸 겁니다. 하튼, 이러한 초기값을 결정하는 것 중에 결정적인 factor가 hash 값이 되고요. 이 해시 값이 모두 같다면, 탐사 시작 위치, 다음 이동 위치 등이 다르지 않을 겁니다. 즉, hash 값을 모두 같은 값으로 해 버리면 충돌이 엄청 많이 일어나는 데이터를 만들 수 있을 겁니다.
이건 java의 hashmap, hashset 등이 쓰는 chaining 방식도 마찬가지입니다.
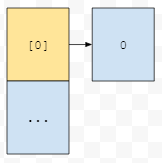
hash값이 모두 0이라서, 같은 버킷에만 계속 들어간다고 해 봅시다. 먼저 0이 0번 버킷에 들어간 상황입니다.
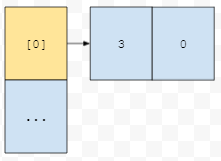
다음에 3이 또 0번 버킷에 들어갔습니다. 어떻게 될까요? 충돌이 매우 많이 나는 최악의 경우를 hashCode 값을 모두 같게 해서 만들 수 있다는 최악의 케이스를 만들 수 있다는 것은, 이러한 의미입니다.

이제 테스트 프로그램을 만들어 봅시다. time과 제가 정의한 Obj를 import 합니다.

그리고 for loop를 돌면서 딕셔너리에 field x가 0부터 sz-1까지인 Obj 객체를 dic의 key로 추가합니다. 그리고 루프를 돌 때 마다, sz 값이 2배가 되는데요.

걸린 시간을 보면 4배로 뻥튀기가 되었어요. sz는 2배로 뻥튀기가 되었는데요. 그러면 복잡도는 O(sz^2)라는 의미입니다. for loop가 돌아가는 횟수가 sz가 되고, 새로 dic 객체를 생성하는 건 상수만에 될 거니까, dic[o] = 1 이 부분이 O(sz)라고 추정할 수 있어요. 어찌 되었던 최악 복잡도는 이 문서에서 설명하는 대로 O(n)이 맞긴 하네요.
다음에는 dict 내부 구조를 이해하기 위해서 필요한 선행 지식인 open addressing에 대해 간단하게 알아봅시다.
'레퍼런스 > 분석' 카테고리의 다른 글
| java 9 부터 도입된 Map.of 메소드를 알아봅시다. (0) | 2022.02.28 |
|---|---|
| java retainAll 메소드를 간단하게 분석해 봅시다. (0) | 2021.11.29 |
| 여러 필드가 있을 때 해시값을 리턴하는 java objects의 hash 메서드를 알아봅시다. (0) | 2021.08.21 |
| java list removeall vs clear : 언제 쓰는지 정확하게 알아봅시다. (0) | 2021.08.09 |
| java string strip 메서드에 대해 제대로 알아봅시다. (0) | 2021.07.31 |


최근댓글