생각난 김에, 간단하게 글을 써 보도록 하겠습니다. 수학 시간에 대우 명제를 써서 증명하는 것은 많이 해 보셨을 겁니다. 이런 걸 대체 ps 문제를 푸는 데 어떻게 쓰는 걸까요? 백준 12858번은 문제가 짧습니다. 구간 s에서 e까지의 수를 t로 바꾼다. 그리고 구간 s에서 e까지 최대 공약수를 구한다.
생각보다 문제에서 요구하는 것은 많지 않습니다. 그러면 이걸 어떻게 풀어야 할까요?
명제 p이면 q이다가 있다고 해 봅시다.

그러면 not Q이면 not P이다 또한 참입니다.
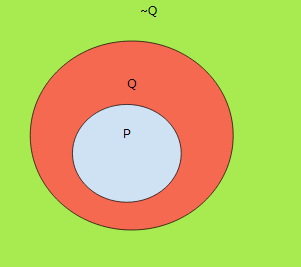
~not P는 ~not Q와 빨간색으로 칠한 부분을 합친 것이기 때문입니다. 보통 P이면 Q다. 라는 명제를 증명하기 어렵지만, ~Q이면 ~P이다를 증명하기가 상대적으로 쉬울 때, 대우 명제를 끌어와서 증명을 많이 합니다.
12858번은 아래 명제를 증명하는 것이 사실상 핵심이라고 보시면 됩니다.
gcd(a(1), ... a(n)) = k일 때, gcd(a(1), abs(a(2) - a(1)), ... , abs(a(n) - a(n-1))) = k이다.
- 명제 A
어떻게 증명해야 할까요? gcd(a(1), ... , a(n)) = k를 조건 p라고 둡시다. 그리고 gcd(a(1), abs(a(2) - a(1)), ... , abs(a(n) - a(n-1))) = k다. 라는 조건을 q라고 둡시다. 그러면, p 조건에 의해서, 1<=i<=n을 만족하는 임의의 i에 대해서 a(i) = k * Q(i)로 둘 수 있습니다.
그런데 만약에, gcd(Q(1), ... , Q(n))의 값이 1이 아니라면 어떨까요? a(i)는 Q(i) * k꼴로 나타낼 수 있기 때문에, 이미 k라는 것을 공통으로 가지고 있습니다.

그런데 Q(1), ... , Q(n)도 u라는 것을 공통으로 가지고 있다면, 사실상 gcd(Q(1), ... , Q(n))의 값은 ku일 겁니다. 혹은, ku의 배수이거나. Q(1), ... , Q(n)의 gcd 값이 1이 아니라고 했기 때문에 u의 값은 1보다 큰 자연수입니다. 그러면, a(1), ... , a(n)의 gcd는 k가 아닙니다. ku인데 u가 1이 아니기 때문입니다.
따라서, Q(1), ... , Q(n)의 gcd 값은 1이 되어야 합니다. 이제 명제 (A)를 보이기 위해서, 우리가 참임을 보여야 하는 명제는 다음과 같습니다.
gcd(Q(1), ... , Q(n)) = 1이라면, gcd(Q(1), abs(Q(2)-Q(1)), ... , abs(Q(n)-Q(n-1))) = 1이다.
- 명제 B
그런데, 걸려 있는 항이 여러개이니 귀찮고 까다로울 듯 싶습니다.
대우 명제를 생각해 봅시다. gcd(...) = 1의 부정은 gcd(...)가 1이 아니다입니다. 이걸 잘 이용하면, 저 명제를 다음과 같이 바꿀 수 있어요.
gcd(Q(1), abs(Q(2)-Q(1)), ... , abs(Q(n)-Q(n-1)))가 1이 아니라면, gcd(Q(1), ... , Q(n)) 또한 1이 아니다.
그러면, gcd(Q(1), abs(Q(2)-Q(1)), ... , abs(Q(n)-Q(n-1))의 값을 v라고 둡시다. 이 때 v의 값은 1이 아닌 자연수입니다. a, b, c, d, e의 최대 공약수가 k라면, a, b, c, d, e는 k의 배수여야 합니다. a도 k로 나누어 져야 하고, b 또한 k로 나누어 져야 하고, c도, d도, e도 나누어 떨어져야 하기 때문입니다.

만약에 하나라도, v로 나눴을 때 나머지가 존재한다면, 최대공약수가 v가 아닐 겁니다. 따라서, Q(1)은 v의 배수입니다. 즉, Q(1) = vq(1)로 나타낼 수 있습니다. abs(Q(2)-Q(1)) 또한 vq(2)로 나타낼 수 있는데요. Q(2)-Q(1) 또한 v의 배수입니다. 즉, Q(2)-Q(1) = vq'(2)로 나타낼 수 있는데, Q(1)을 vq(1)으로 나타낼 수 있기 때문에, Q(2) = v(q'(2) + q(1))으로 나타낼 수 있어요. q'(2)와 q(1)은 정수이기 때문에, Q(2)는 v의 배수입니다.

' 마찬가지로 Q(3)도 봅시다. abs(Q(3)-Q(2)) 또한 v로 떨어져야 합니다. 그러면, Q(3) - Q(2) 또한 v로 떨어져야 하는 건 당연한 이야기입니다. Q(2)가 v의 배수이므로, Q(3) 또한 v의 배수가 되어야 합니다.

만약에 그렇지 않다면, Q(3) - Q(2)는 v(q(3) - q(2)) + r3이 되는데, r3은 0보다 크고, v보다 작은 정수입니다. Q(3) - Q(2)가 v로 떨어지지 않습니다. 조건을 만족하지 않아요. 따라서, Q(3) 또한 v의 배수여야 합니다.

Q(4)에 대해서도 마찬가지로 해 보면, Q(4) 또한 v로 떨어져야 함을 알 수 있어요.

이런 식으로 쭉 보면, gcd(Q(1), ... , Q(n))의 값은 1이 아님을 알 수 있어요. v가 1이 아니기 때문입니다. 대우 명제가 참입니다. 따라서, 대우 명제의 대우 관계인 원 명제도 참이 되고, 우리가 증명하려고 했던 명제 A 또한 참이 됩니다. 그것을 직관으로 찾아내거나, 증명을 해서 찾아내는게 12858번을 푸는 핵심 키라고 할 수 있어요.
자연수 a, b, c가 있습니다. gcd(x,y)는 자연수 x와 y의 최대 공약수를 의미합니다. gcd(a,b) = 2이고, gcd(b,c) = 2일 때, gcd(a,b,c) = 2일까요? 이 명제도 대우 명제를 이용하면 생각보다 깔끔하게 보일 수 있어요.
'자료알고 > 알고리즘' 카테고리의 다른 글
| stable sort : 우선 순위가 같은 데이터들은 어떻게 정렬될까요? (4) | 2019.07.14 |
|---|---|
| 삽입 정렬 알고리즘 : 원소가 들어갈 위치는 어디인가? (2) | 2019.07.11 |
| 냅색 알고리즘 문제 : 가방에 어떻게 넣어야 이득이 최대일까? (0) | 2019.07.03 |
| dfs 심화편 : 깊이 우선 탐색의 단점을 어떻게 보완하는가? (0) | 2019.06.28 |
| 외판원 문제 : 팩토리얼을 지수 복잡도로 낮춰보자 (8) | 2019.06.27 |


최근댓글