dfs, 그러니까 깊이 우선 탐색의 단점은 크게 2가지입니다. 해가 없는 경로에 깊이 빠진다. 그렇기에 유한 시간 내에 끝나지 않을 수도 있다. 그리고, 해를 구했을 때, 그것이 최적이 아닐 수도 있다. 이 2가지 때문에, 보통 최단 거리를 구할 때에는 사용하지 않아요. 그런데, 이걸 잘 보완하면 절찬리에 써먹을 수도 있어요. 절찬리에 잘 써먹을 수 있는 문제 중에 하나를 예로 들어봅시다. 어떠한 세제곱 수를 k개 더해서 n을 만들어야 합니다. k값은 최소가 되어야 합니다. 예를 들어서, 43은 3^3 + 2^3 + 2^3으로 만들 수 있습니다. 물론 1^3을 43개 써서 만들 수도 있지만, 43개보다 작게 만들 수 있는 방법이 존재하기 때문에, 답이 될 수 없습니다.
이 문제는 어떻게 풀어야 할까요? n은 1이상, 44777444 이하입니다. 그리고, 메모리 제한은 8메가라고 했을 때. BFS를 돌리기 위해서는, visit 배열이 필요할 겁니다. 그런데, 상태 수가 상당히 많기 때문에 메모리 초과가 나기 좋을 듯 싶네요. 그러면, DFS, 즉 깊이 우선 탐색을 돌려야 한다는 소리인데요. 아시다시피, DFS는 기본적으로, 최단 경로를 구하기 위한 탐색이 아닙니다. 이 단점을 어떻게 보완하면 좋을까요?
단순히 DFS를 적용한다면 시간 복잡도는 어떻게 나올까요? 1이상 44777444 이하의 n에 대해서, 최소한 9개의 세제곱 수를 쓰면 만들 수 있다는 것은 시뮬레이션을 통해 보일 수 있습니다. 예를 들어, 23은 9개로 만들 수 있어요. 또한, 숫자가 어느 정도 커지면, 5 ~ 6개의 세제곱 수를 넣으면 n이 만들어 집니다. 그러면 depth limit를 5로 잡으면 되겠군요. 해가 없는 경로에 깊이 빠진다는 단점은, 최대 깊이를 정함으로서 해결을 할 수 있습니다. 노드 하나 당 나올 수 있는 자식, 그러니까 다음 상태로 나올 수 있는 것의 갯수는 n^(1/3)개입니다. depth가 5이기 때문에, 사실상 n^(5/3)이 될 건데요. n이 44777444라면 n^1/3의 값은 대략 360이 됩니다. 360^5의 값은 10^12보다 큽니다.
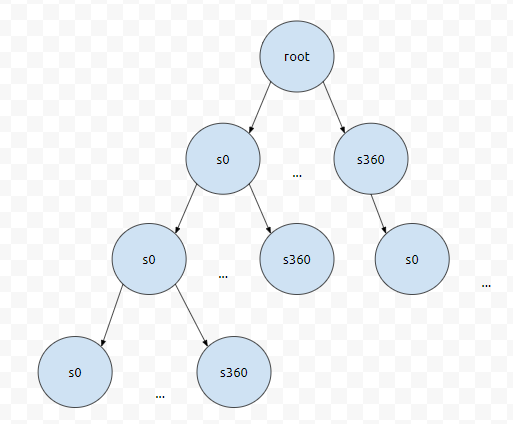
44777444의 해를 구하기 위해서, 어떻게 해야 할까요? 실제로, 답 중 하나는 354^3 + 71^3 + 32^3 + 29^3 + 8^3입니다. 만약에 저 상태로 dfs를 탐색했다가는 꽤 시간이 오래 걸릴 겁니다. 최악의 경우에 거의 360 + ... + 360^5개의 경우를 모두 탐색하기 때문입니다.

예를 들어서, 답 중 하나가 s0, s4, s5, s9, s360이였다고 해 봅시다. 이게 답이 될까요? dfs는 계속 깊게 들어가는 탐색입니다. 그렇기 때문에, 전체 후보들을 탐색하지 않는다면 최단 거리를 구할 수 없어요. 예를 들어, s360, s360이 후보해 중에 하나가 될 수도 있어요. 즉, 경로의 모든 가짓수를 고려해야 하기 때문에, 쓸 수 없습니다.
그러면, 여기서 하나 생각해 볼 수 있는 아이디어는 한 상태 당 뻗어나가는 가지의 갯수를 줄이자는 겁니다.
먼저, a(1)^3, ... , a(k)^3의 합으로 n을 만들었다고 해 봅시다. a(1), ... ,a(n)을 내림차순으로 정렬한다면, a(1) >= a(2) >= ... >= a(n)을 만족할 겁니다. 예를 들어서, 43의 후보해 중 하나인 3, 2, 2를 예로 들어봅시다.
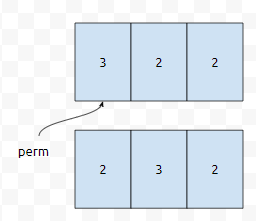
2, 3, 2를 내림차순으로 정렬하면 3, 2, 2가 됩니다. 순서만 바꾼 관계이기 때문에, 저는 이 두 후보해를 '내림차순으로 정렬하면 같다'고 표현을 해 볼 거에요. 즉, 우리는 탐색을 할 때, 큰 세제곱수부터 넣는다는 규칙을 세울 거에요. 예를 들어서, n = 43이라면 3, 3, 2를 넣어 볼 수는 있어도, 3, 2, 3은 넣어볼 수 없습니다. 2 > 3이 아니기 때문입니다.
이렇게만 해도 상태 수는 꽤 줄어드는데, 무엇인가 부족해 보입니다. 예를 들어서 bound가 5입니다. 최대 5개까지 넣을 수 있다고 했을 때, 44777444를 만들어야 합니다.

그러면 제일 큰 세제곱 수가 200^3이라면, 5개의 세제곱수를 넣어서 44777444를 만들 수 있을까요? 아닙니다. 따라서, 200보다 큰 어느 수부터, 360까지가 1번째로 큰 세제곱 수의 후보해가 되어야 할 겁니다. 쭉 돌리다가, 300을 넣었다고 해 봅시다. 300^3의 값은 2700만입니다.
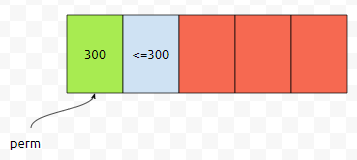
그러면 2번째로 큰 세제곱 수는 300^3보다는 작아야 할 겁니다. 그러면 150^3이 될 수 있을까요? 만약에 2번째로 큰 세제곱 수가 150^3이라면, 다음과 같이 채워져야 할 겁니다.

그런데, 300^3 + 150^3 + 150^3 + 150^3 + 150^3은 44777444보다는 작습니다. 따라서 150^3은 후보해가 아닙니다. 2번째로 큰 세제곱 수는 150^3보다는 커야 합니다. 이런 식으로 후보해가 될 만한 것을 추리면, 10^12개보다 많은 상태수를 탐색하는 게 아니라, depth를 6까지 탐색할 때에도, n이 44777444일 때의 답을 구하기 위해서, 2억개 정도의 상태만 탐색하면 됩니다. depth가 5일 때, 전체 가짓수를 모두 탐색하면 10^12개보다 큰 상태들을 탐색하는데 비해서, 굉장히 빨라진 셈입니다.

먼저, 해를 구하기 위해서, b>mmx보다 큰지 계속 검사하고 있어요. 더 정확히 말하면, b는 얼만큼 더 탐색할 수 있느냐라고 보시면 좋아요. 내가 탐색할 최대한의 깊이만 정해진 경우, 깊이 우선 탐색을 하면서 후보해가 계속 나올 수 있고, 그에 따라서 최적의 해가 계속 갱신될 수 있습니다.
따라서, vaild한 상태 전체를 탐색해야 합니다.

cur-b*i*i*i > 0인 경우 break를 걸어버리고 있는데요. 이것은 최소 bound보다 작으면 break를 걸어버리는 코드입니다. 예를 들어서, n의 값이 44777444이고, 최대 5개까지 세제곱 수를 넣을 수 있다고 했을 때, 그 중 제일 큰 세제곱 수가 100^3이지는 않습니다. 100^3에 5를 곱한 건 고작 500만이기 때문입니다.
그러한 경우를 걸러낸 것입니다. 탐색하는 상태를 더 줄일 수 있는 방법이 없을까요?
dfs는 최단 거리를 구하지 못합니다. 하지만, 어떠한 뎁스까지 탐색을 했을 때, 후보해가 있는지 여부는 모두 검사하지 않고도, 판단할 수 있습니다. 이것을 이용하면 어떨까요?

즉, 깊이 i까지 탐색을 할 건데, 그 i의 값을 순차적으로 증가시키면 될 겁니다. 깊이 i-1까지 보았을 때 해가 없었습니다. 그런데 깊이 i까지 보았을 때 해가 존재했다면, 바로 끝내버리면 됩니다. 그것이 답이기 때문입니다.

실제로 bound 함수의 첫 부분도, b>mmx 이런 게 없습니다. 단지 cur가 0이라면 바로 답을 출력하고 빠져나가버립니다. 이렇게 깊이 제한 탐색을 하면서, 점진적으로 그 제한을 늘려나가버리는 셈입니다.

이런 식으로 처리했더니, 2억번에서 213882개의 상태만 보게 되었습니다. 생각보다 많이 줄어든 셈입니다.
그럼에도, depth = 5까지 본다는 것은 너무 큰 낭비인 듯 싶습니다. depth를 더 줄이는 방법이 없을까요? 사실 제 프로그램은 탐색하는 상태 공간의 최대 깊이가, 복잡도를 결정하는 주된 요인이기 때문에, 이것을 줄이는 방법을 고민해야 합니다. depth를 2개 덜 보는 방법이 있습니다. i^3 + j^3의 값과 (i,j) 쌍을 모두 저장하는 겁니다. 1<= i,j <= 360이므로, 많아봤자 12만 9600개의 숫자만 저장이 됩니다. 이들을 i^3 + j^3이 작은 순서대로 정렬한다면 lower_bound를 쓸 수 있습니다.
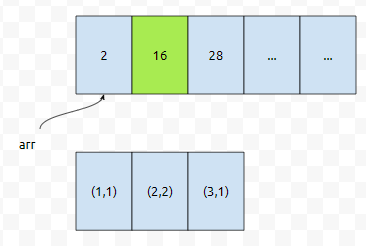
그러면 depth가 2개 남았을 때, arr과 답이 되는 쌍을 참조할 수 있을 겁니다. 만약에, arr에 그 수가 없다면 안 되고요. 그렇게 처리한다면 44777444 이하인, 굉장히 큰 수일 때, 뎁스는 최대 3까지만 보게 됩니다. 그러면 조금 더 효율적으로 처리를 할 수 있습니다. 양방향 탐색 또한 탐색 깊이를 줄인다는 것은 비슷합니다.
깊이 제한을 걸고 dfs를 돌리는 것을 depth limit search라고 하고, 깊이를 늘려나가는 탐색 방법을, iterative deepning search라고 합니다. 간혹 가다가, ps 문제를 풀 때 이런 식으로 처리하면 통과하는 경우가 있어요. 심지어, dfs는 메모리도 그렇게 많이 써먹지 않기도 하고요. 익혀두셔도 좋은 기법인 듯 싶습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| stable sort : 우선 순위가 같은 데이터들은 어떻게 정렬될까요? (4) | 2019.07.14 |
|---|---|
| 삽입 정렬 알고리즘 : 원소가 들어갈 위치는 어디인가? (2) | 2019.07.11 |
| 대우 명제 : 언제 이 도구를 증명하기 위해 쓸까요? (0) | 2019.07.06 |
| 냅색 알고리즘 문제 : 가방에 어떻게 넣어야 이득이 최대일까? (0) | 2019.07.03 |
| 외판원 문제 : 팩토리얼을 지수 복잡도로 낮춰보자 (8) | 2019.06.27 |


최근댓글