부동 소수점에서 결합 법칙은 성립하지 않는다고 합니다. 어떤 경우에 성립을 하지 않을까요? 간단하게 테스트 케이스를 만들어 보도록 하겠습니다.

프로그램 1을 보겠습니다. a가 1.0이고 b가 1.0인데 c는 (2^53)입니다. 그리고 d는 1.0 + (1.0 + 2^53)의 값을 출력하고요. e는 (1.0 + 1.0) + 2^53의 값을 출력해요. 두 값이 같을까요?

결론은 같지 않았습니다. 어떻게 이런 데이터를 만들었을까요? 영어 위키에 있는 문서에 따르면, 64bit짜리 floating point의 경우, fraction 부분이 52 bit라고 해요. 이것을 보고 데이터를 만들었습니다. 뜬금없이 무슨 멍멍이 소리를 하고 있네요. 어떤 의미인지 밑에서 후술하겠습니다.

printDoubleBits입니다. double 자료형에 대해서 최상위 비트부터 최하위 비트까지 보기 쉽게 표현하기 위한 메서드 입니다.

다음에 printDoubleBits인데요. Double의 doubleToLongBits 메서드를 이용했어요.

이 메서드는 value를 IEEE 754 floating point 형식의 bit layout으로 변환합니다. 그렇게 변환한 결과를 가지고 s번째 bit부터 e번째 bit까지 돌리면서 출력해 줍니다.

이제, 1.0, 1.0, 2^53 * (1.0) 순서대로 더해 보겠습니다.

3번째 줄을 보면 0 10...0 0...0 이 부분이 보이실 건데요. 10...0 부분이 지수 부분입니다. 2^0 + 2^0의 값은 2^1입니다. 따라서 지수 부분이 변했음을 볼 수 있어요. 다음에 보셔야 할 부분은 4 ~ 5번째 줄에 있는 수 2개를 더해서 6번째 줄에 있는 수가 나왔다는 것인데요. 이게 어떻게 된 일인지 간단하게 설명해 보겠습니다.
2^-1 + 2^8이 있어요. A2^e 꼴로 표현하려고 해요. 단, A는 1보다 크거나 같고 2보다 작은 실수라 할게요. 어떻게 하면 좋을까요? 2^-1은 (2^-9)2^8와 같다는 것을 이용하면, 2^-1 + 2^8은 (1 + 2^(-9))2^8과 같습니다. 2^1과 2^53을 더하려고 합니다. 어떻게 할까요? 똑같습니다. 2^1은 (2^(-52))2^53 와 같을 것이니, 2^1 + 2^53을 더한 결과는 (2^(-52) + 1)이 될 겁니다.

그러면 대충 요러할 겁니다. fraction에서 51번째 bit는 1/2를, ... , 52-x번째 bit는 1/2^x 를 의미하기 때문입니다.

이제, 2^53, 1.0, 1.0 순으로 더해볼 건데요. 어떻게 더해질까요? 일단, 2^53과 2^0을 더하는 것이니, 결과 값은 (2^(-53) + 1)2^0이 될 겁니다. 여기서 fraction 부분이 2^(-53)이 나와야 할 것인데요.
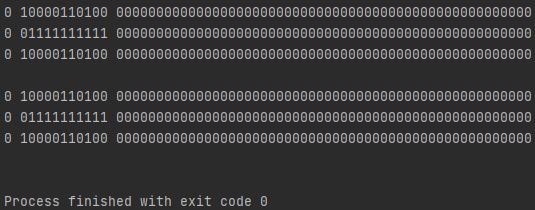
결과는 요래 나와요. 아까와는 다르게 fraction 정보가 사라졌음을 볼 수 있어요. 왜 그럴까요? 간단합니다. fraction을 담는 정보는 52 bit였는데, 1/2^52는 표현이 가능했지만, 1/2^53은 표현을 할 수 없을 정도로 작았기 때문입니다. 이를 이용해서 부동 소수점에서 결합 법칙이 성립되지 않는 데이터를 만들 수 있습니다.
'코딩 > C' 카테고리의 다른 글
| linux makefile과 target을 알아봅시다. (0) | 2022.12.26 |
|---|---|
| 부동 소수점 연산에서 분배 법칙이 성립되지 않는 데이터를 만들어 봅시다. (0) | 2021.12.01 |
| c언어 xor 연산자 ^ 에 대해 간단히 알아봅시다. (0) | 2021.10.08 |
| c언어 배열 포인터 : 배열을 가리킨다. (2) | 2021.03.17 |
| c언어 조건부 전처리기 #if #ifdef 를 알아봅시다. (0) | 2020.12.26 |


최근댓글