부동 소수점은, 가수부와 지수부로 나누어서 저장을 합니다. 즉, (a)*2^b꼴로 저장을 하는데요. 이 때, a는 1보다 크거나 같고, 2보다 작은 실수입니다. 즉, (1.xxx)*2^b 꼴로 저장을 한다는 겁니다. 여기까지는 그리 어렵지 않을 것이라고 생각합니다.
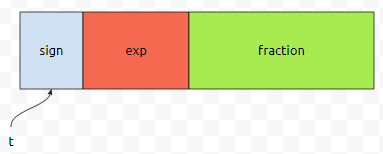
보통 부동 소수점, 우리가 흔히 알고 있는 float이나 double형은 이런 식으로 저장이 됩니다. 지수부랑, fraction. 즉 가수부랑 나누어서 저장을 하고 있는데요. 이 fraction 부분은 (1.xxx)*2^b로 표현했을 때, 0.xxx 부분을 저장한다고 보시면 됩니다. 0.xxx를 2진수로 표현해서 저장할 겁니다.
그러면, 실제로 0.1이 어떻게 저장되는지 봅시다.
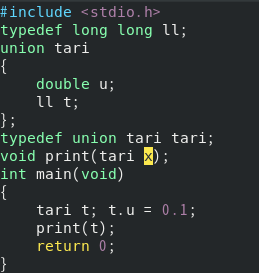
저는 먼저 double과 long long이 같은 메모리 공간을 공유할 수 있게, union을 선언해 주었습니다. 이것을 공용체라고 합니다. 나중에 구조체 하면서 언급할 기회가 있을 듯 싶습니다. 저는 단순히, double형에 0.1을 저장한 다음에, 그 메모리 공간을 long long형으로 읽기 위해서 tari형을 선언했습니다.
t.u에 0.1을 저장하고, print를 합니다.
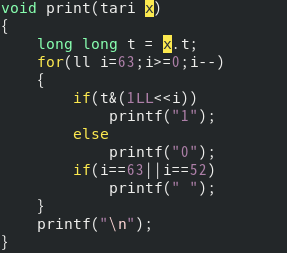
long long형으로 불러옵니다. 그리고 어떻게 저장이 되어 있는지 bit 단위로 출력합니다.

프로그램의 실행 결과는 다음과 같습니다. 0.1이 어떻게 저장이 되었는지 해석을 천천히 해 봅시다. 먼저, 제가 공백으로 끊어 놓은 것을 기준으로 보면, 각각 부호, 지수부, 가수부입니다. 그런데, 지수부에 있는 숫자가 이상해 보이는데요. 실제로 이 값을 찍어보면, 1019가 나옵니다. 0.1은 (2^-4)에 (1.6)을 곱한 값으로 표현할 수 있는데요. 실값에 1023을 더한 셈입니다. 이를 bias라고 합니다.
사실 이것은 별 문제가 없습니다. 하위 52비트는, 가수부인데요. 여기서 문제가 생깁니다.
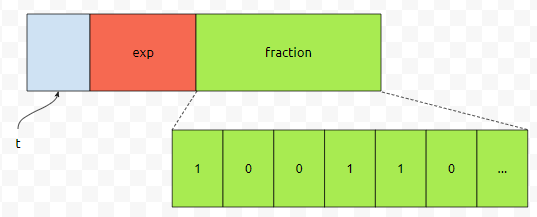
앞에서 0번째 bit의 자릿수는 1/2를, 1번째 bit의 자릿수는 1/4를, ... , k번째 bit의 자릿수는 (1/2^(k+1))를 나타냅니다. 즉, 부동 소수점형 0.1의 fraction 부분은 1/2 + 1/8 + 1/16 + ... 이런 식으로 표현이 됩니다. 실제로, 이것이 double형에서는, 어떤 식으로 표현되는지 봅시다. 간단하게 프로그램을 바꾸면 되는데요.
하위 51번째 bit의 자릿수는 2^51/2^52입니다. 하위 50번째 bit의 자릿수는 2^50/2^52입니다. 이를 이용해서 프로그램을 살짝 수정을 해 봅시다.
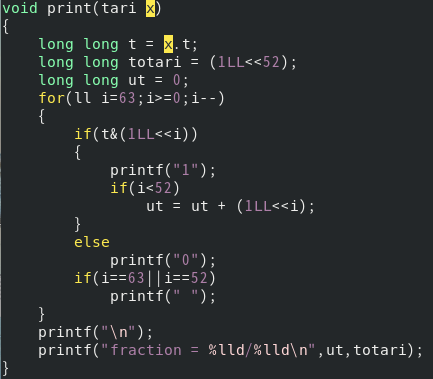
하위 i가 52보다 작다면, i번째 bit의 자릿수가 2^i/2^52를 나타낸다는 것을 이용하면 쉽게 fraction 부분을 분수로 바꿀 수 있습니다. ut는 분자, totari는 분모입니다. 당연하게도, totari는 2^52이니까 처음에 totari는 (1LL<<52)의 값을 넣었습니다.

그러면 실제로 이 fraction 값은 우리가 예상했던 0.6일까요? 아닙니다. 0.6000000000000000888174... 가 나오는데, 이는 실제 값인 0.6하고 오차가 0.0000000000000000888174만큼 납니다.

그러면 이 프로그램의 결과는 어떻게 나올까요? 0.01을 10000번 더했으니까, 100이 출력이 될까요?
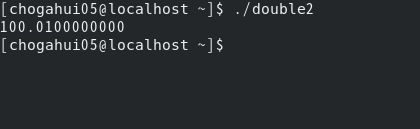
아닙니다. 오차가 발생합니다. 오차가 있는 결과값을 10000번 더했기 때문에 실제 결과값과 차이가 난 셈입니다.
그러면 부동 소수점은 어떤 꼴의 실수를 표현할 때 정확하게 표현할 수 있을까요? 0.625는 어떨까요?

0.625는, 2^-1에 (1+0.25)를 곱한 값으로 표현할 수 있습니다. 즉 fraction은 1/4입니다. 이는 0100... 으로 표현할 수 있습니다. 딱 나누어 떨어집니다. 따라서 0.625는 부동 소수점으로 오차 없이 정확하게 표현할 수 있어요. 이를 일반화 시겨 봅시다.
fraction이 t/r로 표현이 되었다고 해 봅시다. 단, t와 r은 서로소라고 합시다. 그러면, t/r이 Z/2^L꼴로 표현이 되어야 합니다. 단, Z는 0보다 크거나 같은 정수이고, L은 double형의 경우 52일 겁니다. 가수부 필드의 길이 정도라고 생각하면 좋을까요? 이를 Z에 대해서 정리하면, Z = (t*(2^L))/r이 됩니다. 이 Z가 정수가 나와야 하는데요. t와 r은 서로소입니다.

즉, t의 소인수를 t(1), ... , t(k)라고 해 봅시다. 1<=x<=u에 대해서 r(x)는 t의 소인수가 아닙니다. 그러면 결론적으로 빨간색으로 표시한, 그러니까 r의 소인수 집합이 집합 {2}에 포함되어야 합니다.

그러면 r의 소인수 집합은 {}이거나, {2}여야 합니다. 즉, fraction은 t/2^u꼴로 표현이 되거나, 0이여야 합니다. 그렇지 않다면, 2진수로 표현했을 때, 무한 소수로 표현이 될 수 밖에 없어요. 1/3이나, 2/7이나, 1/10을 double형으로 저장해 버리면 실값과 다르게 표현되는 이유는 이 셋은 분모가 3, 7, 10입니다. 이들의 소인수는 각각 3, 7, 2와 5인데, 소인수가 2만 있거나, 아예 없지 않기 때문에, 정확하게 값을 표현하지 못하는 것입니다.
기약분수로 표현했을 때, 분모가 2의 거듭제곱 꼴이 아니라면, 부동 소수점으로 표현하면 오차가 생긴다는 것만 간단하게 정리하고 넘어가시면 좋을 듯 싶습니다.
'코딩 > C' 카테고리의 다른 글
| c언어 double형 vs float형 : 어떤 차이가 있을까요? (2) | 2019.08.06 |
|---|---|
| 1의 보수 vs 2의 보수 : 음수는 어떻게 표현되는가? (2) | 2019.07.28 |
| c언어 단축 평가 : 언제 조건을 볼 필요가 없을까? (0) | 2019.07.02 |
| c언어 비트 이동 연산자 (<<, >>) : 어떤 것을 조심해야 할까요? (0) | 2019.06.26 |
| c언어 비트 연산자 : ps를 하려면 알고 넘어갑시다. (0) | 2019.06.25 |


최근댓글