간혹 가다가, 이런 이야기를 들으실 수 있을 거에요.

사실, 이 용어는 다이나믹 프로그래밍 뿐만이 아니라, 다른 기법에서도 종종 나오니, 고수 분들의 설명을 들으시려면, 정확한 정의는 모르셔도 됩니다. 그냥 아. 이런 거구나. 이해만 하셔도 무난합니다. 솔직하게 말해서, 시험에 나올 일도 거의 없을 겁니다.
간단한 예제를 들기 위해서, 16690번 paper Cuts 문제를 보도록 합시다. 문제를 요약하면 아래와 같습니다.

str이 "abbaaddccee"이고 pat이 aaabbeeddcc입니다. 저는 str에서 칸막이 몇 개를 사용해서 잘게 쪼개려고 합니다. 위 그림에서는 "abb", "aa", "ddcc", "ee" 이렇게 쪼개졌습니다. 칸막이 u개를 써서 잘 쪼갠 문자열들을, 어떻게 잘 배치해서 pat을 만들 수 있을 때, 문자열 str에 가위질을 u번 해서 pat을 만들 수 있다고 이야기 합니다.
위 그림에서 u = 3이고, 가위질을 3번 해서 str에서 pat을 만들 수 있었습니다. str에서 가위질을 최소한으로 해서 pat으로 만드는 게 우리의 목표입니다. 단, str과 pat은 아나그램 관계입니다. 그리고 두 문자열의 길이는 18 이하입니다. 우리가 해결해야 하는 문제는 무엇인가요?

"banana"를 최소한으로 자른 다음에, 어떻게 잘 재배치 해서, "nnaaba"를 만드는 문제를 해결하면 됩니다. 그러면, 이것을 이렇게 생각해 봅시다. 선택할 수 있는 집합은, str의 0, 1, 2, 3, 4, 5번째입니다. 그리고, 만들어진 집합은 pat의 0, 1, 2, 3, 4, 5번째 입니다. 이것을 각각 보라색과 노란색으로 표시해 보겠습니다.

그러면, 그림으로 표시한 이 문제를 풀기 위해서, 어떤 문제를 풀어야 하나요? 먼저, pat을 채울 때에는, 뒤에다가 계속 붙인다고 합시다. 그렇다면, 뒤에 있는 "a"를 택하거나, "ba"를 택하거나, "aba"를 택하거나, "aaba"를 택하거나, "naaba"를 택하거나, "nnaaba" 를 선택하거나. 이렇게 6가지 중 하나가 나올 거에요. 먼저 "a"를 택한다고 해 봅시다.
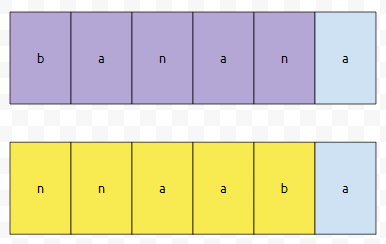
그러면, str의 맨 뒤에 있는 "a"를 선택할 수도 있습니다.

그렇지만 중간에 있는 "a"를 선택할 수도 있어요.

2번째에 있는 "a"를 선택할 수도 있을 겁니다.

끝에 있는 "ba"가 나중에 채워졌다고 한다면 어떨까요? 이 경우에는, 보라색으로 칠한 집합이였던, 0, 1, 2, 3, 4, 5 중에서, "ba"가 있는지를 확인해 보면 됩니다. 보니까, 0번째, 1번째를 선택하면 될 듯 싶군요. "aba", "aaba", "naaba", "nnaaba"는 "banana"의 부분 문자열인가요? 아닙니다. 따라서, "nnaaba"가 된 경우, 마지막으로 "a"를 append 했거나, "ba"를 append 했거나. 이 둘 중 하나임을 알 수 있습니다.
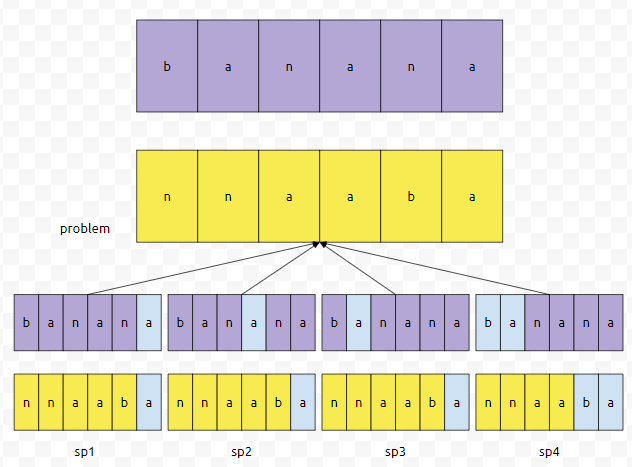
이걸 그림으로 나타내 보면 위와 같습니다. problem을 풀기 위햇, sp1, sp2, sp3, sp4 모두를 알아야 합니다. 그런가요? 그렇다면, sp1, sp2, sp3, sp4는 problem의 부분 문제라고 할 수 있겠네요.
그런데, 하나 더 궁금한 게 있습니다. 메모이제이션. 이것은 대체 무엇일까요? 다시 문제를 보도록 하겠습니다.

sp3을 해결하기 위해서는, sp4를 해결해야 합니다. sp1과 sp2, sp4의 부분 문제들은 지면 관계상 그리지 않았습니다. 그런데, 또 sp4는 problem의 부분 문제란 말이죠. 만약에, sp3을 해결하기 위해서 sp4를 해결했는데, 그 결과를 저장하지 않았다고 해 봅시다. 그러면, problem을 해결하기 위해서 sp4를 해결하려고 했을 때, 계산된 값을 쓰지 않을 겁니다.

sp4를 해결하기 위해서 sp5, sp6을 부르는데요. 계산이 되어 있지 않다면, sp4를 다시 불렀을 때, sp5, sp6 또한 다시 부를 거에요. 계산을 했던 것을 또 하고, 또 합니다. 호출 트리를 그려보면 아래와 같습니다.
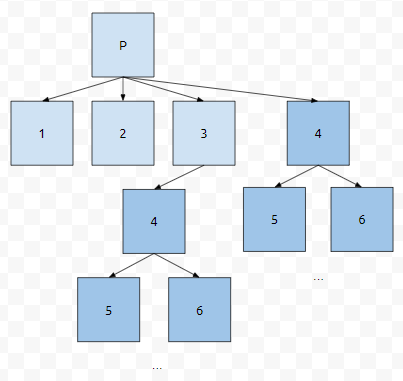
이는 비효율을 의미합니다. 이미 필요한 음식을 만들어 두었는데, 또 만드는 꼴이니까요. 그러면 이것을 어떻게 할까요? 4번 부분 문제에 대한 계산이 끝났다면, 4번 부분 문제에 대한 답이 x다. 라는 것을 배열이나 특수한 자료구조에 저장을 합니다. 그러면 다음에 4번을 만났을 때, 어떻게 하면 되나요?
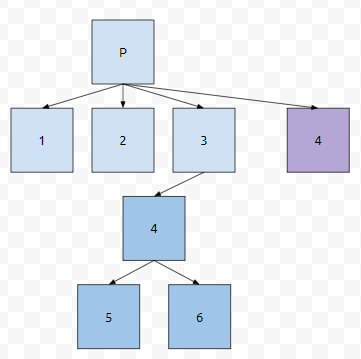
이미 계산된 값을 끌고 오면 됩니다. 이를 메모이제이션 기법이라 합니다. 그러면, 16690번보다 쉬운 연습 문제를 풀어 보겠습니다.

피보나치 수열은 위와 같이 정의됩니다. 이 때 a[n]의 값을 구하고 싶습니다. a[n]을 구하는 문제의 부분 문제는 무엇인가요? 단, n은 대충 100만 정도라고 생각해 봅시다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 좌표 압축 알고리즘 : 범위가 클 때 어떻게 공간을 줄일까요? (4) | 2020.02.22 |
|---|---|
| 백준 balanced cow subsets : 반으로 잘 쪼개 봅시다. (6) | 2020.02.10 |
| 트리에서 최단 경로를 구하기 위한 또 다른 방법? (0) | 2020.02.02 |
| 코테에서 답을 미리 저장하는 방법도 쓸만한가요? 네 (4) | 2020.01.29 |
| 프로그래머스 가장 큰 수 : 수 2개만 고려해 봅시다. (7) | 2020.01.24 |


최근댓글