우선순위 큐는, 삽입과 삭제가 일어날 때, 가장 우선순위가 높은 것을 빠르게 찾을 수 있는 구조입니다. 일단, 이것의 특징 먼저 간단하게 잡고 넘어가 봅시다. 먼저, 부모들은 자식들보다 rank가 높습니다.
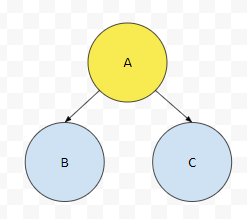
예를 들어서, A의 자식이 B, C라고 해 봅시다. 그러면, A >= B이고 A >= C입니다.

그러면 A의 모든 child들 (자식의 자식이라던지)은 무조건 A보다 rank가 같거나 낮을까요? 위 그림을 봅시다. B(1)의 직계 child는 B(2), B(2)의 child는 B(3), ... 이런 식으로 가고 있어요. 그러면 A >= B(1) >= ... >= B(n)이 성립합니다. 연쇄입니다. 따라서, A >= B(n)입니다. 부모에서 자식으로만 연결된 간선이 있고, x가 A로부터 도달 가능할 때, A의 rank는 x의 rank보다 같거나 큽니다. 이것이 우선순위 큐의 특징이라고 할 수 있습니다. 여기서 하나 약속 하겠습니다.
원소 A가 원소 B보다 우선순위가 높은 경우, 저는 알기 쉽게 A > B로 표시하겠습니다.
먼저 insert 연산을 보겠습니다. 먼저, 말단 노드에 새로운 데이터를 추가합니다. 그러면 그림이 이런 식으로 그려질 거에요.

이 때, p의 우선순위 >= le의 우선순위 입니다. 이것을 간단하게 p >= le라고 표현하겠습니다. 만약에 p >= new라면 그대로 끝내면 됩니다. 그렇지 않고, new >= p라면 어떻게 하면 좋을까요? new >= p라면, new >= le입니다. 왜냐하면 p >= le이기 때문입니다. 처음에 cursor가 말단 노드의 최 우측을 가리치고 있고, 그 위치에 새로운 원소를 추가했다고 해 봅시다. 노랗게 칠한 노드입니다. 부모가 자식보다 rank가 작다면 new >= p인 상황입니다. 따라서, 부모의 rank가 자식인 cursor가 가리키고 있는 것보다 작다면 업데이트를 하고 현재 cursor를 부모로 올려주면 됩니다.
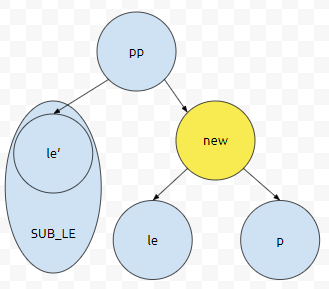
그러면, 이 때에는 어떨까요? 일단 pp의 자식 중 하나가 le'이라고 했을 때, le'를 Root로 가지는 subtree에 있는 모든 노드들은 le'의 우선 순위보다 낮거나 같을 겁니다. 즉, SUB_LE를 대표하는 대장 값이 le'일 거에요. 이것보다 pp의 priority가 크거나 같기 때문에, pp >= le'을 만족합니다. 여기서, pp >= new인 경우 그대로 끝내면 됩니다. new >= pp라면 어떨까요? 그러면 new >= le'입니다. new >= pp 이기도 하므로, 노란색으로 칠한 노드와 부모를 바꾸고 cursor를 위로 올려주면 됩니다.

이런 식으로 cursor가 루트에 도달하거나, cursor의 부모의 rank가 cursor가 가리키는 것의 rank보다 크거나 같은 경우에 break를 걸면 됩니다. 아직 무슨 소리인지 잘 모르겠어요. 사실 저도 처음 배울 때, 이걸 어떻게 구현해야 할 지 몰라서 많이 헤멨던 기억이 납니다. 실전 연습에서 그대로 해 보도록 하겠습니다.
이제 top에 있는 원소를 빼 버렸다고 해 봅시다. 이 때, 단말 노드이면서, 가장 우측에 있는 것을 맨 위로 올려버립니다. top이 있었다고 했을 때, 리프 노드는 하나 지워봤자, priority queue의 특성이 무너지지 않기 때문이에요. 만약에 중간에 있는 내부 노드들을 지웠다고 한다면, 그 특성이 무너집니다. 중간에 있는 것이 비어 있기 때문이에요. cursor는 root에서 시작합니다.

그러면 이 때, 서브트리 L과 R은 우선 순위 큐의 조건을 만족합니다. top 하나가 빠지고 새로운 ntop이 root로 올라온 것이다. 라는 차이밖에 없기 때문입니다. le와 ri 중에서 rank가 높은 것을 구합니다. 즉 현재 cursor의 자식 둘 중에서, rank가 높은 것을 구합니다. 예를 들어서 le가 더 높았다고 해 봅시다.
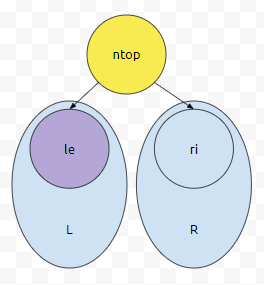
이 때 ntop하고 le하고 비교합니다. 노란색하고 보라색하고 비교를 하는 셈입니다. 만약에 이 le 값이 ntop보다 rank가 높으면 어떻게 해야 할까요? ntop과 le를 바꾸면 됩니다.
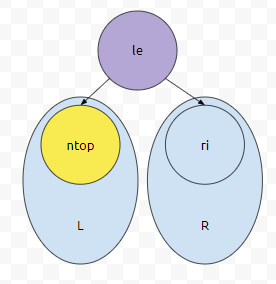
그러면, 이 과정이 수행되고 나서, le, ntop, ri만 보았을 때 이 셋은 priority queue를 만족합니다. 문제는 ntop이 le보다 크기 때문에, ntop이 L의 대표값이 될 수 있는지는 아직 모른다는 것입니다. 그러면 어떻게 해야 할까요?
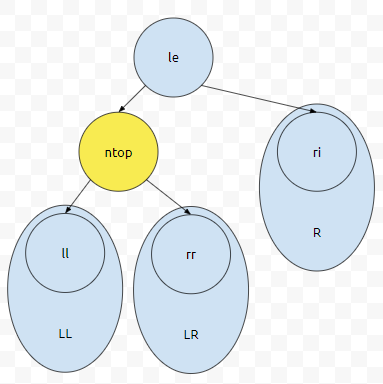
서브트리 L은, LL과 LR과 ntop으로 구성되어 있다고 합시다. LL의 Root를 le를 넣었다면 L은 우선순위 큐의 조건을 만족하였습니다. 그런데 le >= ntop입니다. ntop이 L의 root로 들어가면 조건을 만족할까요? 그럴 수도, 아닐 수도 있어요. 그러면 어떻게 해야 하나요? LL의 대표값은 ntop의 왼쪽 자식, LR의 대표값은 ntop의 우측 자식이 됩니다. 이들은 Heap의 성질을 그대로 유지하고 있기 때문입니다.
그러면 여기서 어떻게 하면 좋을까요? ll과 rr 중에서 rank가 높은 것을 찾습니다. rr > ll이였다고 해 봅시다.

그러면 rr과 ntop을 비교하면 됩니다. 만약에 ntop >= rr이면 어떤가요? 그러면 그대로 끝내면 됩니다. rr > ll이기 때문에 ntop >= ll이기 때문입니다. 그런데 rr > ntop이면 문제가 생깁니다. 자식보다 부모가 우선 순위가 더 작기 때문입니다.
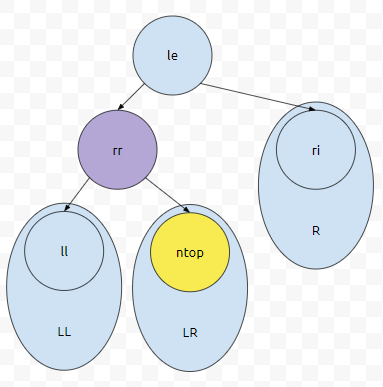
만약에 그렇다면 rr과 ntop이 swap 되면서 cursor도 오른쪽 방향으로 내려갈 건데요. 그렇다면 우리는 LR 서브트리에 대해서만 신경쓰면 된다는 것을 알 수 있어요. 재귀적으로 보면. 이해 가시나요? 현재 cursor에 있는 원소와 두 자식들 중에서 우선 순위가 높은 것을 비교했을 때, cursor에 있었던 것이 더 높다면 그냥 끝내면 되어요.
하지만, 그렇지 않다면, 자식들 중 우선순위가 높았던 친구와 cursor에 있었던 것을 서로 바꾸고, 우선 순위가 높았던 것이 왼쪽에 있었으면 왼쪽 자식으로, 오른쪽에 있었다면 오른쪽 자식으로 커서를 이동시키면 됩니다.
이제 실전 연습 한 번 해 봅시다. 수가 작은 것이 priority가 높다고 해 보겠습니다.

우선 순위 큐에 다음과 같이 데이터가 들어가 있습니다. 여기서 1을 추가하려고 합니다.

리프의 맨 오른쪽에 1을 넣습니다. 그런데 이 때, 부모인 2는 1보다 우선 순위가 낮습니다. 그러면 어떻게 해야 하나요? 부모와, 노란색 부분을 바꾸면 됩니다.

그러면 1과 2가 바뀝니다. 이 때, 노란색 부분도 당연하게도 위로 올라와야 겠네요. 다음에, 노란 노드와, 그 부모 노드의 priority를 비교합니다. 비교했는데 1 >= 1인가요? 즉, parent가 child의 우선순위보다 같거나 커요. 따라서, 이 때에는 바꾸지 않고, break를 합니다.

top을 꺼낸다면, 맨 위의 root가 비어 있습니다. 이 때 어떤 것을 끌어 올려야 하나요?

말단 노드, 그 중에서도 가장 오른쪽에 있었던 2를 올립니다. 그러면 아래와 같이 될 거에요.
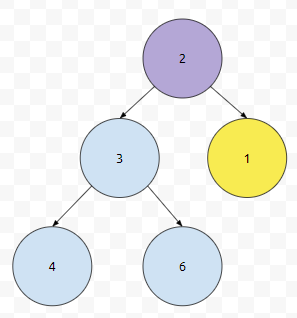
이 때, 보라색으로 칠한 것들의 child들 중에 rank가 높은 것은 1입니다. 제가 노란색으로 칠한 녀석입니다. 이것과, 2를 비교했을 때 어떤 것의 rank가 높나요? 1의 우선순위 >= 2의 우선순위 입니다. 따라서 둘을 서로 바꿉니다.

다음에 보라색 부분을 봅시다. 이들의 자식들과 보라색으로 칠한 것 중 우선 순위가 높은 것을 체크해 보아야 하는데, child가 없습니다. 따라서, 이 때에는 그대로 끝내면 됩니다. 우선순위 큐 구조에 대해서는 이 정도만 챙기셔도 무난할 듯 싶어요. 다음 시간에는 이 자료구조를 이용해서 heap sort를 해 보도록 하겠습니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| 비트 배열 : 공간을 1/8, 1/32, 1/64로 압축한다. (9) | 2019.12.24 |
|---|---|
| 스파스 테이블 (sparse table) : 2의 거듭제곱 단위로 점프한다. (4) | 2019.12.20 |
| k번째 숫자 구하기 : 트라이(Trie) 구조를 이용해 봅시다. (2) | 2019.12.05 |
| 프로그래머스 크게 만들기 : 쿼리 특징을 잡아봅시다. (4) | 2019.11.27 |
| 완전이진트리 vs 포화이진트리 : 이 둘에 대해 알아봅시다. (7) | 2019.11.09 |


최근댓글