이번 시간부터는 약간씩 고급진(?) 자료구조들을 배워보려고 합니다. 그 중, 첫 번째는 어떻게 희소행렬 (sparse matrix)를 표현할 것인가? 입니다. n행 m열의 행렬이 있다면, nm개의 수를 가지고 있을 거에요. 그것에 비해, 0의 수가 월등하게 많다면 어떻게 해야 할까요?
예를 들어, 1000 by 1000 행렬에, 1이 10개만 있고, 나머지는 모두 0이라고 해 봅시다. 그러면, 인접 행렬로 10^6개의 수들을 모두 저장할 필요가 있을까요? 그렇지 않다는 것이 핵심입니다.
그러면 어떤 정보를 저장하면 좋을까요? r행 c열에 수 k가 있다. 그러면, 이러한 정보를 동적 배열에 넣어버리면 될 겁니다. 예를 들자면, 1행 1열에 1, 1행 3열에 1, 2행 2열에 15가 있는 5 by 5짜리 행렬 A를 생각해 봅시다.
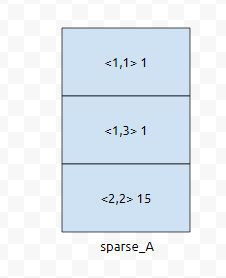
그러면 이렇게 저장을 할 수 있습니다. 이것을 깡 행렬로 표현했다면 어떻게 표현이 되었을까요?
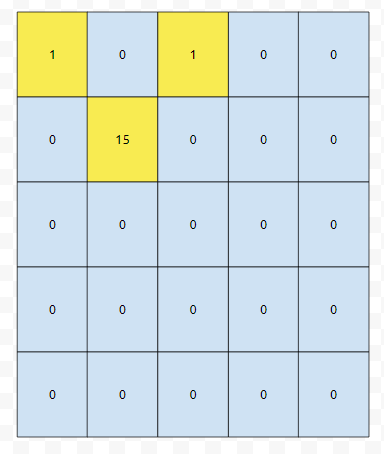
한 행당 5개의 수를 저장하고, 5개의 행을 가지는 2차원 배열을 선언해야 할 겁니다. 분명한 것은 노란색으로 칠한 것만 의미있는 정보라는 것입니다. 나머지 22개는 의미 없는 정보들입니다. 의미 있는 정보들만 추려서 저장을 한 것인데요. 비슷한 아이디어를 쓰는 것이, 좌표 압축이라는 기법입니다. 이것은 추후에, ps나 알고리즘에서 다시 언급해 드리도록 하겠습니다.
곱하기는 다소 어려우니, 덧셈만 먼저 언급하도록 하겠습니다. Transpose랑, 곱셈은 다음에 설명하겠습니다. matrix A와 matrix B는 행 오름차순으로, 행이 같으면 열 오름차순으로 정렬이 되어 있습니다.
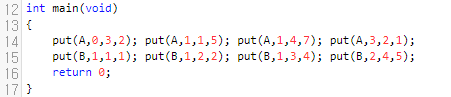
보시면, <행, 열> 순서대로 들어갔음을 알 수 있어요. 그러면 add는 어떻게 할 것이냐. 간단합니다. 우리는 비교체를 하나 정의를 할 건데요. 행이 같으면 열로 비교를 할 거에요. 그러면 아래와 같이 compare를 작성해 주시면 됩니다.
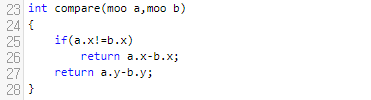
보시면, <a.x, a.y>가 <b.x, b.y>보다 작을 때에는 -1을, 같으면 0을, 크면 1을 리턴함을 알 수 있어요. 이 함수를 토대로, 우리는 add 함수를 작성해 보겠습니다.
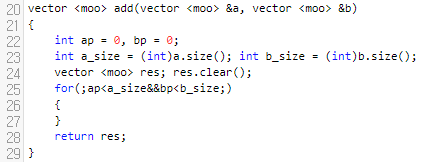
일단 큰 for loop를 작성해 줄 건데요. 이것은 행렬 A의 원소들과 행렬 B에 있는 원소들을 다 순회하지 않았을 때 처리를 해 줄 거에요.

먼저 ap는 <1,1>을, bp는 <2,1>을 가리키고 있어요. compare를 돌려보니까, ap가 가리키고 있는 <행,열> 쌍이 bp가 가리키고 있는 것보다 명백하게 작습니다. 따라서, ap가 가리키고 있는 것을 결과에 넣고, ap의 값을 하나 증가시킵니다.
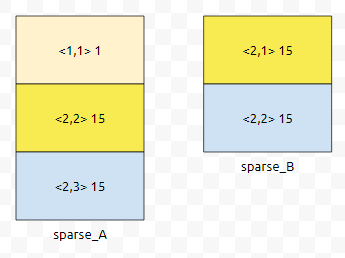
ap가 가리키고 있는 것은 <2,2>입니다. bp가 가리키고 있는 것은 <2,1>입니다. ap가 가리키고 있는 것보다, bp가 가리키고 있는 게 더 작으므로, bp가 가리키는 것을 res에 넣고, bp를 하나 증가시킵니다.

만약에 ap가 가리키는 <행,열>과 bp가 가리키는 <행,열>이 같으면 어떻게 하면 좋을까요? 이 때에는 노란색으로 칠한 두 녀석의 합을 구해서 넣으면 됩니다. 즉, <2,2> 30이라는 데이터를 res에 넣으면 됩니다.

그 다음에 보니까, A와 B 중 하나를 순회 완료했습니다. 그냥 빠져 나오면 됩니다. 이것을 그대로 코드로 구현해 보겠습니다.

여기까지는 무난한 듯 보입니다. 그런데 문제는 ap나 bp가 끝까지 가지 않았을 경우입니다. 즉, A를 모두 순회하지 않았거나, B를 모두 순회하지 않았을 경우인데요. A를 다 순회하지 못했다는 것은 무슨 의미일까요?
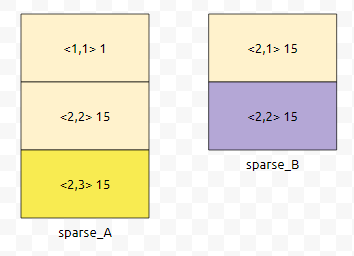
이 경우는 A를 모두 순회하지 못한 겁니다. 왜 그랬을까요? <2,3>이 <2,2>보다는 크기 때문입니다. <행,열> pair에 따르면요.
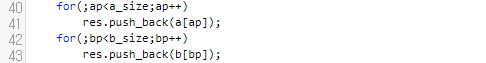
따라서, 아직 행렬을 모두 순회하지 않았다면 마저 탐색하는 문장들을 추가해 주어야 합니다. 눈치를 채셨다면, 병합 정렬의 합병하는 부분과 매우 유사함을 알 수 있어요. 다음 시간에 Transpose와, 곱셈에 대해서 해 보도록 하겠습니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| 완전이진트리 vs 포화이진트리 : 이 둘에 대해 알아봅시다. (7) | 2019.11.09 |
|---|---|
| 전치 행렬 (Transpose matrix) : 왜 중요한가? (2) | 2019.10.13 |
| LRU 알고리즘 : 리스트를 활용해서 구현해 봅시다. (6) | 2019.09.23 |
| 평방 분할 (Sqrt Decompositon) : 루트로 쪼개보자. (2) | 2019.09.22 |
| 재해싱 (rehashing) : 시간 복잡도를 분석해 보면서 왜 필요한지 알아봅시다. (4) | 2019.09.13 |


최근댓글