오늘은 힙 정렬, Heap sort에 대해서 배워보도록 하겠습니다. 어렵지 않으니, 천천히 따라오시기만 하면 됩니다. 저번에, 우선순위 큐라는 자료구조를 배우셨을 거에요. 이 구조를 이용해서 정렬한 것입니다. 이게 끝입니다. 어렵지 않죠? 제가 우선순위 큐를 설명했을 때, 깜빡 잊은 것이 하나 있어요. 이것은, 이진 포화 트리를 만족한다는 것입니다.
그렇기 때문에, 트리의 깊이는 log(들어간 원소의 갯수)에 비례합니다.
그러면, 이것을 어떻게 구축할지가 문제입니다. Root를 0번 인덱스라고 합시다. 그리고 0번의 자식은 1, 2번이라 합시다. 그리고 1번의 자식은 3, 4번이라 합시다. 즉, 어떠한 노드 k가 있다면, 그들의 child는 2k+1과 2k+2가 됩니다.

그러면, 우선 순위 큐에 들어가는 원소의 갯수가 최대 n개라면 몇 개의 노드가 필요할까요?
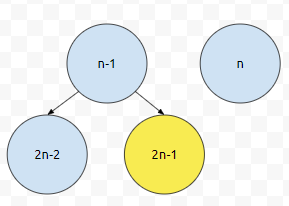
2n개가 필요합니다. 그냥 넉넉하게 2n + 10개 정도의 노드를 할당합시다. 그런데 이 노드들 번호만을 가지고 배열로 관리할 수도 있을까요? 어짜피 우리는 뒤에서만 추가되는 형태입니다. 그렇기 때문에, 정적 배열로 관리해주면 될 거에요.
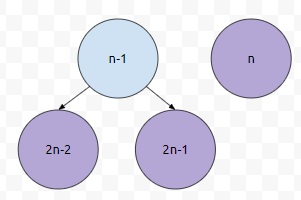
그러면, 보라색 부분은 사실 우리가 쓰지 않는 노드입니다. 여기에 DUMMY 값을 채워야 하는데요. 우선 순위가 가장 낮은 것으로 채웁니다. 예를 들어서 Min Heap을 구현해야 하고, Heap 구조에 수가 [0, 10억] 범위 내에서만 들어온다면, 보라색 부분을 20억으로 초기화 시켜주면 됩니다.

그러면, 어떠한 수를 pop 하고, 다시 build하는 과정을 생각해 보았을 때, 자식 둘과 현재 위치를 비교해서 바꾸면 됩니다. 어짜피, 현재 위치에 있는 수가 20억보다 낮아질 일이 없기 때문입니다. 더미 노드를 활용하는 것은 상당히 중요한데요. 만약에, 그렇지 않으면 자식이 1개만 있는 경우, 2개만 있는 경우, leaf인 경우. 이렇게 3가지를 고려할 수 밖에 없어요. 코드가 다소 길어지고 복잡해 집니다. 이를 피하기 위해서는, 2n + 10개의 노드들을 모두 할당해 둔 다음에, 처음에 우선 순위가 제일 낮은, inf로 초기화를 시켜주어야 합니다. DUMMY를 이용한 기법은 생각보다 많이 쓰이기 때문에 알아두면 상당히 유용한 TRICK입니다.
그리고 처음에 초기화를 할 때, heap_sz는 0이라는 것을 알 수 있는데요. 그 이유는 나중에 설명해 드리도록 하겠습니다.
push 먼저 구현해 봅시다. 먼저 cur는 heap_sz번째 원소를 가리키고 있습니다. 이 위치에 x를 추가합니다. 그리고 cur 값은 heap_sz가 됩니다. 이게 대체 무엇을 하는 것인지는 밑에서 설명드리도록 하겠습니다.

그러면 보라색 값이 cur번째 원소입니다. 이것과 parent를 비교할 건데요. parent는 어떻게 구하면 될까요? floor((cur-1)/2)입니다.
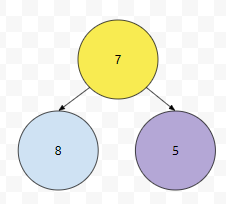
parent는 노란색, 현재 위치는 보라색입니다. 보라색 우선순위가 노란색 우선 순위보다 큰 경우, 둘을 바꿉니다. 그렇지 않거나, 현재 보라색이 root의 위치라면 break를 걸어버리면 됩니다. 위 그림의 경우, 7이 5보다는 priority가 작기 때문에 둘의 위치를 바꿉니다.

그리고 cur은 부모로 올라갑니다. 언제까지 이것을 해야 할까요? cur의 parent보다 현재 cur의 우선순위가 더 낮거나 같을 때 까지 반복해 주면 됩니다. 예를 들어 이런 경우에는 어떨까요?

MIN HEAP의 경우 부모가 현재 위치에 있는 것 보다는 priority가 높거나 같습니다. 따라서 여기서 끝내면 됩니다. 그러면 heap의 조건을 만족할 수 있습니다. 그리고 heap_sz를 하나 증가시키면 됩니다. 제가 설명한 부분을 그대로 소스 코드로 옮겨 보겠습니다.

그렇게 복잡하지는 않네요. 이제 가장 우선 순위가 높은 것을 빼는 연산이 남았어요. 그런데 top 연산과 pop 연산이 구분되어 있는 게 편할 거 같습니다. 그렇기 때문에, 저는 이 둘을 다 구현하도록 하겠습니다.
먼저 top은 어렵지 않습니다. 우선 순위가 제일 높은 것은 Root, 그러니까 0번째에 있기 때문에 heap[0]을 돌려주면 됩니다.

문제는 pop 연산이 들어온 경우입니다. 이 때에는 어떻게 해야 할까요?

맨 끝에 있는 것을 Root로 올린다고 했어요. 삭제하기 전에 heap_sz 값이 10이였다면, heap[9]이 맨 끝에 있는 값인 셈입니다. 따라서, 먼저, heap_sz 값을 하나 감소시킵니다. 그러면 heap_sz가 노란색으로 칠한 7을 가리킬 겁니다.

이 값을 root에 넣습니다. 즉, heap[0]에 7을 넣습니다.

그리고, 현재 pointer가 0번째 원소를 가리키게 합니다. 여기까지 코드를 봅시다.

이런 저런 셋팅을 다 하고 나면, 이제 root에 있는 것을 heap의 특성에 맞게 재조정 하는 일만 남았습니다. 우리는 더미 노드라는 존재 때문에, child 2개와 현재 위치에 있는 것을 비교하는 것만 고려하면 된다고 그랬는데요.

현재 cur의 위치를 군청색, 자식들 중에서 우선순위가 더 높은 걸 노란색으로 표시했습니다. 이 파란색하고 노란색하고 비교했을 때, 노란색이 더 높으면 둘의 위치를 바꿉니다.

그리고 cursor는 왼쪽 자식이 priority가 더 높았다면 왼쪽으로, 그렇지 않다면 오른쪽으로 이동합니다. 언제까지 LOOP를 돌면 될까요? 당연하게도, 부모의 우선순위가 자식들의 우선순위보다 높을 때 끝내면 됩니다. 2n + 10개의 노드를 set 하면, leaf인 경우와, child가 단 1개만 있는 경우, 둘 다 고려하지 않아도 되기 때문에 조금 더 단순해 졌어요.
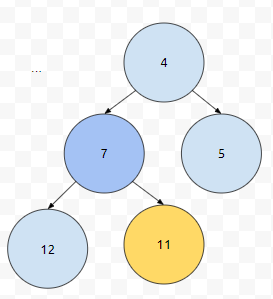
이 경우에 어떻게 하라고 했나요? MIN HEAP이라면 그냥 끝내면 됩니다. 이를 반영한 코드입니다.

보시면 자식들의 우선 순위에 따라서, ch 값이 결정된다는 것을 알 수 있어요. 우리는 heap[cur]하고 heap[ch]를 비교하는데요. 이 때, heap[ch]는 두 자식 중 priority가 더 높은 쪽입니다. 만약에 현재 위치가 자식들보다 더 중요하다면 그냥 빠져나오면 됩니다. 그렇지 않으면 바꾸고, cur를 잘 이동시키면 됩니다.
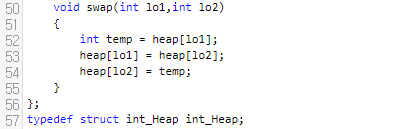
swap은 어렵지 않아요. 힙의 lo1번째 원소와 lo2번째 원소를 서로 맞바꾸는 일만 합니다. 그러면 이걸 가지고 뭘 할까요?
간단합니다. 정렬은, 우선순위가 높은 것에서 낮은 순으로 재배열 하는 것을 말합니다. 그렇기 때문에, 해당 자료구조에 원소들을 다 넣고, 하나씩 꺼내 오면, sorting이 되는 것입니다.

시간 복잡도는 Heap을 rebuild하는데 걸리는 시간에 n을 곱한 O(nlogn)이 됩니다. 이는, push를 할 때에도, cur가 변할 때, 1 깊이 하나만큼 변하고, pop을 해서 root로부터 내려갈 때도 1 깊이만큼 들어가기 때문이에요. 포화 이진 트리에서 depth는, log(n)에 비례합니다. 어떠한 데이터가 들어와도 O(nlogn)이기 때문에, Quick sort에서 depth가 깊어지면, 힙 정렬로 바꿔버리기도 합니다. 인트로 소트라고 불리는 정렬이 그렇게 sort를 합니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 백준 11691 lcm(i,j) : lcm과 gcd의 관계를 이용한 역발상이 필요하다. (8) | 2019.12.31 |
|---|---|
| 백준 팰린드롬 진법 : 후보해는 생각보다 많이 적다. (10) | 2019.12.21 |
| 0-1 bfs 알고리즘 : 가중치가 0과 1만 있을 때 최단거리는 어떻게 구할까요? (0) | 2019.12.12 |
| 등차수열에서 중간에 빠진 수 구하기 : binary search 기법으로 풀면 된다. (4) | 2019.12.10 |
| 백준 회의실 배정 : 가능한 space를 최대한 크게 만들자. (6) | 2019.11.27 |


최근댓글