오랫만입니다. 가희와 함께 하는 3회 코딩 테스트 때문에 작년 연말부터 글이 꽤 뜸하게 올라왔습니다. 이것이 어제 끝났으니, 문제들을 하나 하나씩 리뷰해 보도록 하겠습니다. bfs나 dfs를 배우다 보면, 방향성이 없는 (다시 말해서, 양방향 간선만 있는) 그래프에서Component 라는 것이 나오게 됩니다. 이 문제가 대표적인 예입니다. 이것을 bfs나 dfs로 찾을 수 있다고 하는데요. 이것을 왜 찾을까, 찾아서 어디에 써 먹을 건지. 이 두 가지 의문에서 나온 것이 제가 출제한 가희와 베개 문제입니다.
아래 그림을 보면 Component는 2개가 있어요. 여기에 있는 간선들은 양방향으로 연결된 친구들입니다.
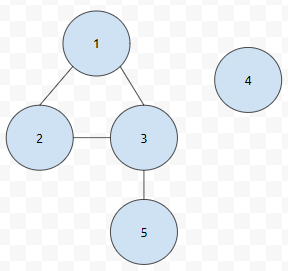
1번에서 bfs를 돌려 봅시다. 1번을 큐에 넣어볼까요?
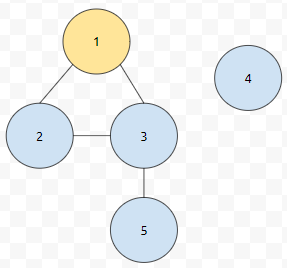
그러면 큐에는 1만 들어가 있을 거에요. 큐의 맨 앞에는 1이 있으므로, 1을 pop 하고, 1과 인접한 친구들을 큐에 넣어요.

그러면 2와 3이 큐에 들어갑니다. 2와 3은 1과 인접하기 때문입니다.

이제 2를 빼면서 탐색하게 되는데요. 1과 3이 인접해 있어요. 1과 3은 갈 수 있는 친구이긴 한데요. 이미 1, 3은 방문을 한 상태입니다. 따라서, 큐에서 제거만 하게 됩니다.
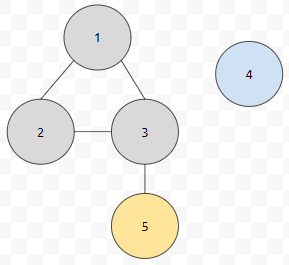
다음 큐에서 3을 뺀 다음에 인접한 친구들을 모두 볼게요. 1, 2, 5가 있는데요. 1, 2는 방문했으니 또 방문을 하지 않고, 5만 새롭게 방문하게 됩니다. 그러면 1에서 갈 수 있는 친구들은 1, 2, 3, 5인 것이 맞나요? 맞습니다. 왜 그럴까요? a에서 b로 가는 것이 가능했고 b에서 c로 가는 것이 가능하면, a에서 c로 가는 게 가능하기 때문입니다.
그러면 반대로 5에서 1로 가는 것도 가능한가요? 이것 역시 가능합니다. 왜냐하면, a에서 b로 가는 간선이 있을 때, b에서 a로 가는 간선 또한 있기 때문입니다. b에서 c로 가는 것이 있을 때, c에서 b로도 갈 수 있는 간선이 있기 때문입니다. 이를 일반화 시키면, i에서 j로 가는 방법이 있을 때, j에서 i로 가는 방법이 있습니다. 결국 서로 방문할 수 있는 얘들끼리 묶는다는 목적이 들어간 셈입니다.
제가 출제한 이 문제 또한 모두 양방향 간선만 존재합니다. 즉, undirected graph의 특성을 가집니다. 그렇기 때문에, component끼리 묶으면 컴포넌트 안에 있는 위치들 끼리는 가희가 이동을 할 수 있습니다. 예를 들어, 예제 2번을 적당히 잘 묶어 봅시다.
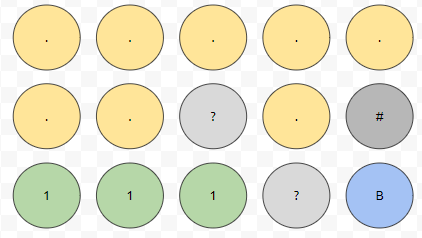
그러면 요렇게 묶어낼 수 있습니다. 어떻게 묶었는가? 가희가 경사로를 아무것도 설치하지 않았을 때를 가정하고 묶었습니다. 이 때, 예제 2번은 아래와 같이 압축이 될 수 있습니다.

아직 아무런 간선도 연결되지 않은 상태입니다. ?로 표시된 위치에 경사로를 설치할 수 있다고 하였습니다. 경사로를 적절히 설치해서 고도 1과 고도 0인 지점을 이을 수 있다는 말을 다시 풀어서 쓰면, 경사로를 설치했을 때 간선이 나올 수 있다는 의미입니다. 예를 들어, 2행 3열에 남쪽 방향의 경사로를 설치했다 해 봅시다. 그러면 노란색과 연두색을 이으므로, 이런 그래프가 나오게 될 겁니다.

다음에 3행 4열에 있는 ?에 W 방향의 경사로를 설치하면 연두색과 군청색을 이을 수 있어요.
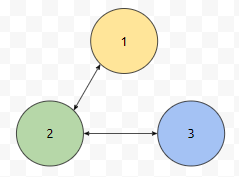
가희가 1번 컴포넌트에 있고, 3번에 베개나 가방이 있으니, 가희가 적절히 경사로를 설치해서 갈 수 있습니다. 경사로를 설치해서 간선을 잇는 가짓수는 많아봐야 2가지가 나오게 되므로, 고려해 보아야 하는 가짓수는 2^18개가 됩니다. 물론, 고려해야 하는 가짓수가 2보다 작은 경우에는 적절한 더미 데이터를 넣어서 2가지를 채우는 센스있는 코딩을 하시면 조금 더 쉽게 풀이가 가능하셨으리라 생각해요.
그런데, 여기서 의문이 하나 남아요. 2^18가지의 가짓수에 대해서 컴포넌트가 많으면 대략 738^2개 만큼 나올 텐데 이렇게 하면 시간 초과가 나지 않을까요?
여기서 생각보다 매우 적은 component만 방문한다는 사실을 관찰한다면, 그렇게 해도 됨을 알 수 있어요. 우리가 쓸 수 있는 간선은 많아봐야 18개입니다.
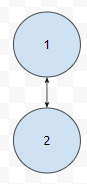
1에서 출발했다고 하겠습니다. 간선 하나를 써서 2를 방문했어요. 그러면, 이 과정에서 방문한 수는 2개입니다. 다음에 간선 하나를 써서 1과 2가 아닌 다른 녀석을 방문했다고 하겠습니다.
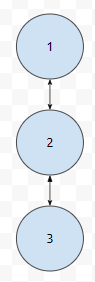
그러면 2개를 썼는데, 3개를 방문해 버립니다. 이를 일반화 시키면 간선을 i개만큼 썼을 때 최대 i+1개만을 방문한다는 것을 알 수 있어요. 그러면 최대로 방문하는 컴포넌트 개수가 19개라는 건가요? 네. 그렇습니다. 심지어 하나의 간선이 관여하는 컴포넌트는 2개이므로, 38개의 컴포넌트에 대한 정보만 잘 관리하면 됩니다.
2^18가지의 가짓수에 대해서 많아봐야 100개 이하의 정보만 가지고 돌리면 되므로 시간 내에 돌아가게 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 백준에서 자주 보이는 절대 오차 상대 오차에 대해 간단하게 알아봅시다. (0) | 2022.01.31 |
|---|---|
| 가희와 쓰레기 놀이 : 메타 정보를 잘 저장해서 효율적으로 구현해 봅시다. (2) | 2022.01.28 |
| 가희와 비행기 문제를 카탈란 수로 구해 봅시다. (0) | 2022.01.06 |
| 롯데 자이언츠와 가희 : 벤다이어그램을 그려서 도식화 시켜 봅시다. (0) | 2021.11.24 |
| sort 함수의 custom compare 함수를 구현할 때 어떤 점도 조심해야 할까요? (0) | 2021.11.10 |


최근댓글