1달 2주 정도만에 자료구조 포스팅으로 돌아왔습니다. 와아아~. 생각난 김에, 안드로이드의 sparse Array에 대한 이야기를 해 보도록 하겠습니다. 당장 android의 스파스 어레이를 구글에 검색해 보시면 HashMap 하고 비교하는 글도 많아요. 거기서 빠질 수 없는 주제는 성능 비교일 텐데요. 퍼포먼스 이야기는 여기서 굳이 하지 않겠습니다. 이 포스팅을 보신 다음에, 추가적인 질문을 통해서 생각을 해 보도록 합시다.
sparse는, 분포된 정도가 적은, 희박한이라는 뜻을 가집니다. 이것이 array의 수식어가 되면 어떨까요? 희소 배열. 즉, 전체에서, 정말 중요한 몇 % 정도만 저장하고 있는 구조 정도로 생각하시면 됩니다. 그런데, 사실 수식어가 걸리는 대상이 더 중요합니다. 여기서, 걸리는 대상은 Array입니다. 배열은 어떤 특징을 가지나요?

1 앞에 6을 insert 한다고 해 보겠습니다.

그러면 군청색으로 칠한 부분이 뒤로 밀려납니다. 다음에, 1을 삭제한다고 해 보겠습니다.
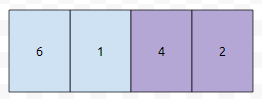
그러면 보라색 부분이 앞으로 당겨질 겁니다. 일반적인 배열은 insert, delete가 최악의 경우에, 배열의 크기만큼의 복잡도가 걸려버립니다. 물론, 메모리를 통째로 복사하는 함수를 쓰면 상수가 낮아지겠지만요. 그런데, 하나 더 문제가 있습니다. 배열은, 사실 랜덤 엑세스에 강한 구조입니다. 인위적으로 배열이 되어 있는 array에서 어떠한 값을 찾으라는 쿼리가 들어오면 이 역시 배열의 크기만큼 순회를 해야 합니다.
예를 들자면, 아래와 같은 배열에서 11을 찾는다고 해 보겠습니다.

11이 없다는 걸 알기 까지는 5개의 원소를 순회해 봐야 합니다. 결국 insert, delete, find 연산 모두 최악의 경우 O(array_size) 만큼 걸리는 게 일반적인 array라고 할 수 있겠습니다. 그런데, insert는 모르겠지만, 뒤에 2개의 연산은 optimize를 할 수 있습니다.
먼저, delete를 보겠습니다.
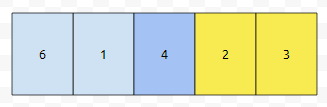
[6, 1, 4, 2, 3]이 있습니다. 여기서, 4를 지우려고 합니다. 상식적으로 생각해 보면, 뒤에 있는 2와 3이 앞으로 당겨져야 할 겁니다. 그런데, 앞으로 안 당기게끔 할 수 있습니다. 추가적인 자료구조를 이렇게 정의해 보겠습니다.

이렇게 정의한다면, 2번째 위치, is_removed[2]를 true로 바꿔주기만 하면 된다는 것을 알 수 있습니다.

그러면 일단 어떠한 위치를 delete 하는 쿼리는 O(1) 정도만에 해결이 될 수 있다는 것을 알 수 있습니다. 여기서 문제는, 어떠한 Key값을 삭제한다, 이러한 Query가 들어온 경우입니다. 예를 들어, [6, 1, 4, 2, 3]에서 4가 삭제된 상태에서, 다음에 10을 삭제하라는 쿼리가 들어왔다고 해 보겠습니다.
[6, 1, 4, 2, 3]에서 10을 찾기 위해서 어떻게 해야 하나요? 그냥 순회를 할 수 밖에 없습니다. sorting이 된 Array에서는 binary search가 가능합니다. 예를 들어, 이런 경우입니다.

여기서 11을 삭제한다는 쿼리가 들어왔다고 했을 때에는 어떻게 하면 될까요? 반씩 쪼개서 들어가면 됩니다. (0+5)/2는 2니까, arr[2]를 볼 건데, 이 값이 3이니까, 이것보다 큰 위치에 11이 있을 겁니다.

정확하게 반절씩 쪼개서 들어가기 때문에, Key값을 찾는 것은 O(log(배열 크기)), 삭제 하는 것은 mark만 하면 되므로 O(1)입니다. 따라서, 삭제 쿼리는 O(log(배열 크기))에 퉁칠 수 있습니다.
is_removed가 1인 필드들을 garbage라고 이야기 합니다. 쓸모 없는 값이라는 소리입니다. 이것을 굳이 들고 있는 이유는 삭제가 되었을 때, marking만 하기 위해서입니다. 그러면 재활용은 못 할까요?

배열 [1, 2, 3, 4, 6, 12]에서 지워졌다는 maring이 3번째, 4번째에 있다고 해 보겠습니다. 이 상태에서 key 5를 추가한다고 가정해 보겠습니다. 어떻게 하면 좋을까요? 5보다 크거나 같은 최초의 위치를 연두색으로 표시해 보았습니다.
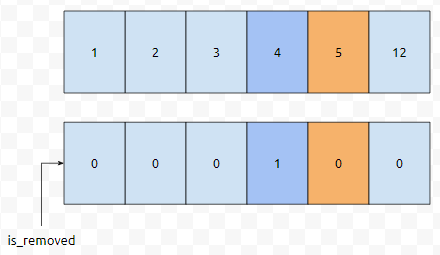
이 값을 5로, is_removed를 0으로 업데이트 하면 어떨까요? 5보다 크거나 같은 최초의 위치인 4번째가, 실제로는 비어 있었다는 것입니다. 비어 있었던 자리라면, 그냥 들어가기만 하면 됩니다. 따라서, 4번째 위치에 5를, 4번째의 remove flag를 0으로 다시 setting 하는 것입니다. 한 가지 상황을 더 드리겠습니다.

그러면 이 상태에서, 5라는 Key를 추가한다면 어떨까요? 5보다 크거나 같은 최초의 위치는 4입니다. arr[4]의 값이 9이기 때문입니다. 그리고, 9는 5보다 크고, 비어 있지 않기 때문에, 연두색 앞에 5가 들어가야 하는 그림이 만들어 집니다.

그러면 보라색 2개가 뒤로 밀려야 되는 상황이 그려집니다. capacity가 6입니다. 그런데. 하나가 추가되지 못하는 상황입니다. 그러면, expand 연산이 일어나게 될 텐데요. 아시다시피 동적 배열에서 expand operation은 상당히 비싼 연산 중 하나입니다. 이를 최대한 회피하려면, is_removed 플래그가 켜진 것들을 최대한 제거하고 보아야 하는데요. 이를 gc를 한다고 하겠습니다. 쉽게 말해, 쓰레기들을 회수하는 작업입니다. minor gc와 꽤 유사한 상황임을 눈치 채신 분도 계실 겁니다.

그러면, 위와 같이 될 겁니다. 배열의 크기가 5가 되고, capacity는 그대로가 됩니다. 그리고 is_removed[0], ... , is_removed[4]의 값은 0이 됩니다. 삭제된 것들은 모두 밀었기 때문입니다. 이 상황에서, key 5를 추가한다. 어떻게 될까요?

5보다 크거나 같으면서 삭제되지 않은, 것들 중 제일 작은 값은 9입니다. 이 9가 있는 위치는 3번째입니다. 그러면 3번째부터 4번째까지가 뒤로 밀려야 합니다.

그러면 배열이 이런 식으로 될 거고, 초록색으로 칠한 자리에 Key 5가 들어갑니다.

그러면, insert 연산은 최악의 경우에 O(배열의 크기) 라고 생각하시면 될까요? 키를 찾는 거나 삭제하는 것은 O(log(배열 크기))이고요. 삭제가 된 것들은 marking이 되고, insert를 할 때 공간이 부족하다 싶을 때 gc가 수행된다. 그리고 insert는 키가 들어갈 수 있는 자리가 삭제된 곳이다. 그러면 marking만 해제하고, 그렇지 않으면, 들어갈 자리부터 맨 끝까지 뒤로 1칸씩 민다고 보시면 되겠습니다.
이제, 링크의 코드를 분석하실 수 있을 겁니다. 500줄이라 다소 깁니다. 이 글에서 설명하지 않은 내용들도 있을 겁니다. 하지만, 큰 흐름을 보면 딱히 다르지는 않습니다. 분석을 해 보시고, HashMap이나 TreeMap과 비교했을 때 어떤 메리트가 있는지도 곰곰히 잘 생각해 보시면 좋겠습니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| 스택계산기 구현 : 연산자 우선순위와 결합 순서만 생각해 봅시다. (2) | 2020.07.02 |
|---|---|
| java에서 STL의 multimap 구조를 구현해 봅시다. (2) | 2020.06.24 |
| trie에서 공간을 줄이기 위해 포인터를 어떻게 쪼갤까요? (0) | 2020.05.05 |
| 랜덤 접근이 가능한 deque 자료구조를 chunk로 구현하면 어떤 이점이 있을까요? (6) | 2020.04.07 |
| 세그먼트 트리 구조에서 lazy propagation을 적용하는 코드를 뜯어봅시다. (0) | 2020.03.31 |


최근댓글