이번 시간에는 백준에서 문제를 푸실 때 많이 보이는 절대오차, 상대오차에 대해서 간단하게 짚고 넘어가도록 하겠습니다.
먼저 모범 답안과의 절대 오차가 x 이하이면 정답 처리한다는 말이 무슨 이야기일까요? 실제 정답이 a라고 하면 a-x를 출력해도 정답, a+x를 출력해도 정답이라는 의미입니다. 즉, 내가 출력한 답을 b라 하고, 실제 답을 a라 하면 abs(b-a)의 값이 x이면 정답이라는 의미입니다.
1008번 문제를 보도록 할게요. a/b를 출력하라고 하는데요. 절대 오차 또는 상대 오차가 10^(-9) 이하이면 정답이라고 해요. a = 4, b = 3을 입력받았어요.
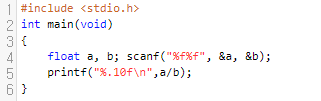
float로 받아서 float 형식으로 출력했어요.

1.3333333731이 출력되네요. 실제 답은 1.3333333333... 인데요. 실제 답과의 절대 오차가 0.000000040.. 이 됩니다. 절대 오차가 4 * 10^(-8)만큼 차이나므로, 절대 오차가 10^(-9)이하가 아닙니다. 그러면 상대 오차가 10^(-9) 이하일까요? 절대 오차와는 다르게, 상대 오차는 배율로 생각하면 편해요.
예를 들어서, 원래 답과의 차이가 +-10%까지 허용한다. 그러면 상대 오차는 10^-1까지 허용하는 셈입니다. +-1%는요? 상대 오차는 10^-2까지 허용한다는 이야기입니다. 그러면, 원래 답 1.333333333... 과 실제 출력한 값 1.3333333731의 상대 오차는 얼마일까요? 1.3333333731에서 1.3333333333... 과의 차이를 대략 0.00000004로 근사해서 계산해 봅시다.

그러면 요래 나오는데요. 0.00000003배율만큼 차이가 난다는 의미입니다. 이것은 10^(-9)보다 크므로 상대 오차로 처리해도 오답 처리가 됩니다.
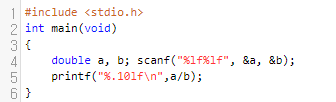
그러면 어떻게 해야 할까요? 정밀도가 더 큰 자료형으로 바꾸면 됩니다. float보다는 double의 정밀도가 더 큽니다. 그러니, float 대신 double로 바꿔 보겠습니다. a = 4, b = 3을 입력받았습니다.
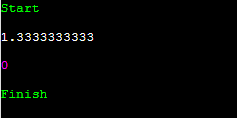
그랬더니 어떤가요? 1.3333333333... 에서 1.3333333333을 뺀 결과값은 float와 비교하면 많이 작음을 알 수 있어요. 앞의 10자리가 같음을 볼 수 있는데요. 이것은 절대 오차가 10^(-9)보다는 작다는 이야기입니다. 그러니 double로 처리하고, 소수점 10자리 이하까지 출력하게 하면 정답 처리가 됩니다.
이제 제가 가희와 무궁화호 문제를 모종의 이유로 실수 민감형에서 실수 오차 허용형으로 바꾸었는데요. 어떠한 처리를 했는지 설명해 보도록 하겠습니다. spj는 기대하는 값과 유저의 output 값을 받아서 조건대로 동작하는지 테스트를 하는 코드를 작성해야 해요. 저는 실수 오차 허용 spj를 셋팅해 본 적이 없어서 검수진 분들의 도움을 받았습니다.
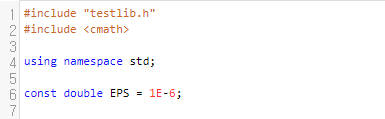
먼저 절대, 상대 오차는 10^(-6)까지 허용한다고 되어 있으므로 EPS는 1E-6으로 적어줍니다.

다음에, j와 p를 받는데요. 모범 답안과 유저가 제출한 답안의 output을 의미합니다. 여기서 doubleCompare를 썼는데요. 이게 어떻게 동작하는지 codeforce의 testlib.h를 찾아서 이 부분을 읽어 보았습니다. 크게 3 부분으로 나뉘는데요.

이 부분은 들어오는 result가 inf나 nan인지 검사합니다.
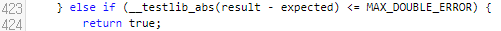
다음에, 이 부분은 result와 expected의 절대 오차를 검사하는 부분임을 알 수 있어요.
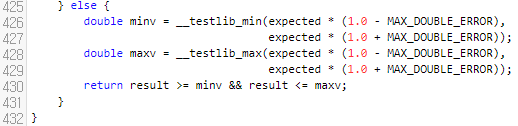
다음에 이 부분은 1.0 +- MAX_DOUBLE_ERROR가 있어요. 상대 오차임을 알 수 있네요. 즉, doubleCompare는 절대, 상대 오차 중 하나를 만족하면 참임을 알 수 있습니다. 제가 셋팅한 가희와 무궁화호 문제에서 예제 1의 1번째 답이 89.3972602739...입니다. 그런데, 89.3973으로만 출력해도 정답 처리가 됩니다. 이건 왜 그럴까요? 절대 오차부터 구하면, 0.0000402...가 됩니다. 즉, 절대 오차 조건은 만족하지 않아요. 그러면 상대 오차는 만족하는가? 상대 오차는 답에 비해 몇 배율만큼 차이나는지가 중요한데요. 0.0000402에 89.3972602739...를 나누면 아래와 같이 나옵니다.

이는 허용 범위인 10^(-6)보다 작으므로 정답 처리가 됩니다.
여담. 이 문제의 첫 버전은 실수 민감형이였는데요. 표정 속도를 a라 했을 때, a를 소수점 첫째 자리에서 버림한 값을 구해야 하는 것이였습니다. 얼핏 보면 지금 버전과 별 차이가 없어 보이지만, 무시무시한 함정이 있었습니다. 왜냐하면, 옥천 - 대전간의 거리가 16.2km이고 이 구간을 12분에 주파하는 데이터에서 문제가 터질 수 있거든요.
이렇게 실수 민감형으로 주어지는 경우에는, 어떻게 해야 할까요? 주어지는 데이터를 실수로 받아버리면 안 됩니다. ddd.d꼴로 주어진다면, 이것을 정수 단위로 parsing 할 생각을 해야 합니다. m로 받던, 100m 단위로 받던. 헷갈리지 않게 받는 방법은 23.7km 라는 데이터가 주어졌을 때, 23700으로 받으면 좋겠네요. 저는 237로 받았습니다.

python으로 받는 경우, 이런 식으로 parsing 하면 간단하게 하실 수 있습니다.

다음에, 표정 속도를 구할 때, 적절한 수식을 써서 계산해 주시면 됩니다. 이 부분은 링크에서 보실 수 있습니다. 모종의 이유로 실수 민감형에서 실수 오차 허용형으로 바뀌었지만, 유념해 두실 필요는 있는 듯 싶어서 따로 작성해 보았습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 실수 오차의 무서움과 가희와 방어율 무시 (0) | 2022.09.05 |
|---|---|
| 가희와 프로세스 2 : 관점을 바꾸어서 이분 탐색을 적용해 봅시다. (0) | 2022.02.21 |
| 가희와 쓰레기 놀이 : 메타 정보를 잘 저장해서 효율적으로 구현해 봅시다. (2) | 2022.01.28 |
| bfs나 dfs에서 component를 왜 구하는지 알아보고 응용해 봅시다. (0) | 2022.01.24 |
| 가희와 비행기 문제를 카탈란 수로 구해 봅시다. (0) | 2022.01.06 |


최근댓글