가희와 방어율 무시 문제는 상당히 쉬운 문제였습니다. 그럼에도 불구하고 정답률이 그렇게 높지 않았는데요. 실수 오차 때문에 고전하는 경우가 상당히 많이 있었습니다. 이와 비슷한 이슈가 있었던 문제 중 하나는 가희와 btd5가 있었습니다.
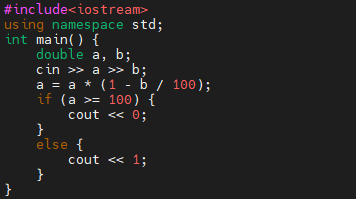
먼저, 오답 코드는 위와 같습니다. 물론, 백준 질문에도 올라왔던 코드입니다. 어느 케이스에서 틀렸을까요?

500 80에서 제대로 답을 출력하지 못합니다. 왜 그럴까요? 실수 오차 때문이다. 라는 것을 누구나 알 수 있습니다. 어떠한 과정에서 잘못된 결과가 나왔는지 하나씩 보겠습니다.

먼저 1, b/100, c에 대해서 bit 값을 출력해 보겠습니다.
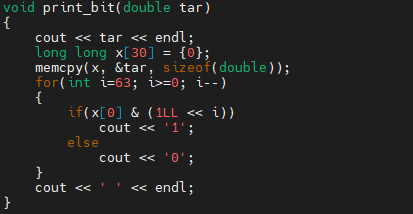
저는 memcpy 등으로 변수를 배열에 복사한 뒤에, 저장되어 있는 값의 bit를 하나씩 꺼내왔습니다.

저는 b, b/100, 1 - b/100의 값을 뽑았습니다. 여기서 주목해야 할 것은 0.8이 정확하지 않은 값으로 뽑혔다는 것입니다. 8/10은 (1 + 0.6)에 1/2를 곱한 값과 같습니다. 따라서, 0.8의 실수부는 0.6이 나오게 될 겁니다. 10011001100 ... 이 부분이 0.8의 실수부입니다. 그이 둘을 빼는 과정을 봅시다. 1과 0.8의 지수부가 다르기 때문에 지수부를 먼저 맞춥니다.

그러면 위는 1.00000이고, 아래는 .110011001 ... 입니다. 이 둘을 빼면 .00110011...이 됩니다. 그런데, 아직 정규화가 되지 않았네요? .110011001... 에다가 8을 곱하면, 1.10011001... 이 됩니다. 그렇다는 이야기는 반대로 지수부는 3만큼 빠져야 한다는 소리겠죠?

그래서 1-b/100 이라고 하는 것은 이렇게 나올 겁니다. 이제 여기에 500을 곱해 봅시다.

0.2에 500을 곱하면 뭐가 나올까요? 이것도 쉽진 않겠지만 해 봅시다. 먼저, 0.2의 가수부가 10011001... 꼴입니다. 500은 어떨까요? 500/256은 256(1 + 0.953125)으로 표현이 가능합니다. 따라서, 가수부는 1111 0100 ... 정도가 되겠네요. 지수부를 알고 있고, 가수부를 알고 있기 때문에 결국 (1 + .10011001...)과 (1 + .11110100)을 곱하게 되는데요.
.10011001... 이 문제가 되기 때문에, 계산된 100의 실수부 또한 정확하게 나오지 않습니다. 더 정확히 말하면 (1 + .10011001...)이 (1 + 0.6)보다 작습니다. 그리고 (1 + .11110100)은 (1 + 0.953125)입니다. 우리는 (1 + 0.6보다 약간 작은 값)/8과, 256(1+244/256)을 곱하게 되는데요. 이는 100보다 약간 작은 값입니다. (1.6)/8에 256(1+244/256)을 곱한 값이 100이기 때문입니다.

그렇기 때문에 우리가 알고 있던 실수 값 100보다 작게 나오게 됩니다. 이런 케이스 때문에 오답을 뱉게 된 것입니다.
그러면 어떻게 처리해야 할까요? 정수로 바꿔서 처리하면 됩니다.

여기서 실수 오차가 날 만한 것이 있나요? 있을 수도 있습니다. a가 정수, b가 정수이기 때문에, 사실상 a * (100 - b)는 정확한 정수 값으로 떨어지게 됩니다. 그리고 여기에 100을 나눈 수치는 실제로 내가 몹에게 느끼는 체감 방어율의 정수 부분입니다. 이 값이 x보다 크거나 같다면, 최종적으로 나타나는 a 값도 x보다 크거나 같을 겁니다. 따라서, 해당 코드는 정답을 출력하게 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 가희와 프로세스 2 : 관점을 바꾸어서 이분 탐색을 적용해 봅시다. (0) | 2022.02.21 |
|---|---|
| 백준에서 자주 보이는 절대 오차 상대 오차에 대해 간단하게 알아봅시다. (0) | 2022.01.31 |
| 가희와 쓰레기 놀이 : 메타 정보를 잘 저장해서 효율적으로 구현해 봅시다. (2) | 2022.01.28 |
| bfs나 dfs에서 component를 왜 구하는지 알아보고 응용해 봅시다. (0) | 2022.01.24 |
| 가희와 비행기 문제를 카탈란 수로 구해 봅시다. (0) | 2022.01.06 |


최근댓글