ps를 하시면, 많이 보는 자료구조 중 하나는, Java에서 TreeSet, TreeMap, C++의 STL에서는 Map, Set 등이 있습니다. 균형 트리로 구현이 되어 있다는 이야기는 많이 합니다. 이게 무엇일까? 에 대해서만 간단하게 생각해 보도록 하겠습니다. 필기 시험에 나올 때 상당히 매력적인 보기를 주는 경우도 있으니, 간단하게 개념을 짚고 넘어가시는 것도 좋겠습니다.
이진 트리를 생각해 봅시다. 이것은 기준 노드를 기준으로 그것보다 작으면 왼쪽에, 크면 우측에 옵니다.
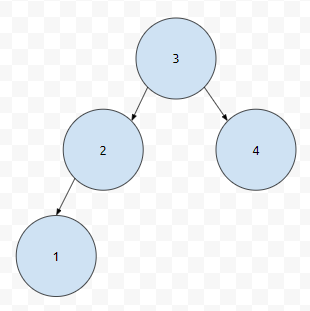
그러면 1을 찾기 위해서는 몇 번의 탐색이 필요할까요? 3보다 작으므로 왼쪽으로 갑니다. 2보다도 작으므로 왼쪽으로 갑니다. 그랬더니 1이 있습니다. 3번 탐색하면 됩니다.

그러면 이 트리에서 -5를 찾기 위해서는 어떻게 해야 할까요? 3, 2, 1, -5 순으로 탐색을 해야 할 거에요. 그런가요? 트리에서 부모 u에서 자식 v로 가는 경로는 유일합니다. 그러면, root에서, 자식 v로 가는 경로 또한 유일합니다. 어느 노드 k의 레벨은 root로부터 k까지 가는 경로의 길이입니다.
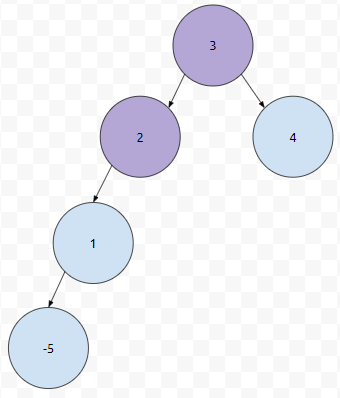
예를 들자면, 2의 레벨은 1이 됩니다. 3으로부터 2까지의 거리가 1이기 때문입니다. 각 노드별로, 노드 번호와 루트로부터 거리, 즉 레벨을 적어 놓겠습니다.

여기서, <> 안에 들어간 수는 루트로부터 해당 노드까지의 거리입니다. 즉 각 노드의 레벨인 셈입니다. 이들 중 최댓값은 3입니다. 여기에 1을 더한 값을 트리의 높이라고 합니다. (3이 맞는지 4가 맞는지는 헷갈리긴 합니다.) 그러면, Binary Search Tree에서 어떠한 수를 찾는 데 걸리는 최악의 시간은 Tree의 height와 연관이 있다고 생각하면 되나요? 맞습니다.
그러면 균형 트리가 무엇일까요? '균형 상태'가 아닌 경우에 자동으로, balanced한 상태를 만들어 주는 무언가라고 생각하면 좋습니다. 예를 들어서, balanced factor가 -1, 0, 1이여야 한다는 제약이 있다고 해 봅시다. 그렇다면 어떻게 될까요? 너무 영어 용어가 나오니까 어려운 듯 싶군요. 간단하게 생각해 봅시다.

노드 3만 생각해 봅시다. 왼쪽에 subTree의 높이가 0, 오른쪽 Sub 역시 0입니다. 이 둘의 차이를 balanced factor라고 생각하는 게 합리적일 거에요. 그러면 3의 균형 지수는 0이 됩니다. vaild 합니다.
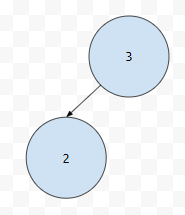
이 때에는 어떤가요? leaf는 무조건 left와 right의 높이 차가 0입니다. 따라서 vaild 할 수 밖에 없고요. 3을 봅시다. left sub에, 2짜리가 하나 달려있습니다. 오른쪽에는 없네요. 따라서, 3의 균형 지수는 1이 됩니다.
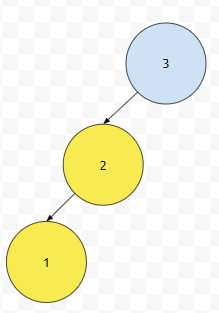
이 경우에는 어떨까요? 왼쪽으로는, Root를 1로 하는 높이 1의 서브 트리가 있고, 우측에는 트리가 없어요. 그렇다면, balance factor는 2 - 0 = 2가 됩니다. 이는 {-1, 0, 1}에 속하지 않아요. 조건을 만족하지 않기 때문에, '균형을 잡힌 상태' 로 만들어 줍니다. 그냥 일반 바이너리 트리 같았으면 그냥 계속 넣을 겁니다.
구글에 Tree 자료구조에 어떻게 원소가 insert가 되고 delete가 되는지 애니메이션으로 보여주는 사이트가 있습니다. 440, 430, 420, 410. 이렇게 4개의 원소가 들어간 상태라고 해 봅시다.

그리고 400을 추가했을 때, 일반적인 bst 같았다면 이 과정에서 끝났을 겁니다. 그런데, 이 경우 'AVL Tree에서 요구하는 밸런스 요건'에 맞지 않습니다. 그렇기 때문에, 이 과정에서 끝나지 않고, rotate와 같은 재구축 과정을 거칩니다.
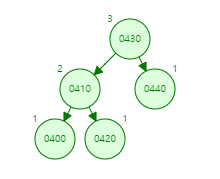
조정이 되니까 어떤가요? 최소한 skew가 되는 상황은 피할 수 있습니다. 만약에 그런 처리가 없었다면 390, 380, ... 이런 식으로 계속 감소하는 수들이 들어온 경우에 한 쪽으로 skew가 되어 버리는 트리가 만들어 졌을 겁니다. 조금의 눈치가 있었다면, 조건이 생각보다 상당히 빡빡하다는 것을 알 수 있는데요. 그런 경우에, 어떠한 데이터를 add하고 delete 했을 때, 조건을 만족하지 못하는 경우가 발생하기 쉽습니다.
그렇게 되면, 데이터를 추가하거나 제거할 때, 재구축 연산을 할 가능성이 높아질 겁니다. 탐색만 고려한다면 나쁘지는 않겠지만, insertion하는 것과 delete 하는 것이 공짜는 아닙니다.
Java에서 TreeMap, TreeSet 도 균형 트리의 일종입니다. 이들은 레드 블랙 트리를 씁니다. 이것은 Tree에 속한 임의의 노드를 보았을 때, 그 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차가 {-1, 0, 1} 셋 중 하나일까요? 이 포스팅에서 코드를 뜯어볼 수는 없는 노릇이니, red/black simulator 사이트에 들어가서, 어떤 식으로 들어가는지만 간단하게 보도록 하겠습니다.
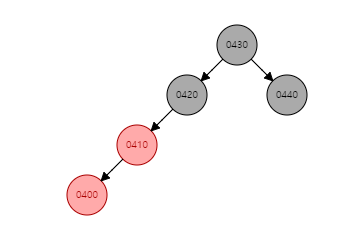
440, 430, 420, 410 순서대로 들어갔다고 해 봅시다. RB tree의 대표적인 조건 중 하나는, Red가 연속으로 나올 수 없다는 것인데요. 새로 추가된 400이 Red입니다. 그리고 그것은 410의 자식이 될 건데요. balanced가 되기 위한 조건에 위배가 됩니다. 일반적인 이진 트리 같았으면 여기서 끝냈을 겁니다.
하지만 추가적으로 다시 rotate라던지, 색깔을 다시 입히는 작업까지 합니다.

다시 말해서, RB Tree의 balanced 조건에 맞게 고치는 과정을 거칩니다. 즉 자가 균형 bst인 셈입니다. 그러면, 그 다음에 390, 405까지 추가하면 어떻게 될까요? 시뮬레이션을 사이트에서 돌려보니 아래와 같이 나왔습니다.

아까 본 어떤 트리와는 차이가 다소 있는 듯 싶어요. 제약 조건이 다르기 때문에 그렇습니다. 그렇기 때문에, 같은 데이터를 넣었을 때, Tree의 모양 또한 다르게 나올 수 있습니다. 정리해 봅시다. 균형 트리는 일반적인 bst와 같습니다. 그렇지만 추가적인 제약 조건이 있어서, 그 조건을 만족하지 못하면, 추가적인 연산을 합니다. 그렇게 해서, 'balanced 조건' 또한 맞춰 나가는 자료구조다. 정도로 생각하시면 좋겠습니다. sort 상태를 유지하면서, self balanced한 대표적인 구조는 AVL과 RB가 있는데요. 제약 조건이 다르기 때문에, 균형 트리의 높이는 최대 [log2(n)] + 1이다. 이러한 것이 무조건 맞다고 생각하시면 안 되겠습니다.
'자료알고 > 자료구조' 카테고리의 다른 글
| 누적된 변환과 lazy propagation 알고리즘 (4) | 2020.02.29 |
|---|---|
| c++ set이나 map을 전체 순회하는 데 시간 복잡도는 얼마일까요? (4) | 2020.01.31 |
| 비트 배열 : 공간을 1/8, 1/32, 1/64로 압축한다. (9) | 2019.12.24 |
| 스파스 테이블 (sparse table) : 2의 거듭제곱 단위로 점프한다. (4) | 2019.12.20 |
| 우선순위 큐 : 부모가 자식들보다 rank가 높다. (0) | 2019.12.16 |


최근댓글