오늘은 기수 정렬에 대해서 알아보도록 하겠습니다. 이것은 키 2개를 가지고 비교하는 정렬이 아닌데요. 이 특성은 저번에 배운, counting sort의 '2개의 키 값을 비교'하는 '비교 기반 정렬이 아니다' 라는 성질을 가지고 있습니다. 이들과, merge sort는 키 2개를 직접 비교하는 비교 기반 정렬이냐, 아니냐의 차이가 있어요. 아래 두 개의 글을 잘 보셔도 눈치를 채실 수 있을 듯 싶습니다.
[관련글]
빈도를 저장하는 counting sort. 알아봅시다.
그러면, 이것은 어떻게 동작할까요?
저는 1가지 용어만 정의하겠습니다. b진법으로 잡고 정렬한다. 버킷의 갯수가 b개이다. 우리는 양의 정수를 표현할 때, x진법으로 표현할 수 있습니다. 예를 들어 370은 10진수로 370입니다. 100이 3개 있고, 10이 7개 있고, 1이 0개 있는 수입니다.
그러면, b = 100이라면 370은 100이 3개 있고, 1이 70개 있다. 이런 식으로 표현이 가능할 거에요. 저는 일단, b = 10이다. 라고 생각해 보겠습니다. 그러면 자릿수의 범위가 [0, 10)이니까, 버킷의 갯수도 10개가 나올 거에요. 저는 배열 arr을 정렬할 건데요. [0, 91, 21, 2, 9, 11]이 들어가 있습니다.

처음에는 이런 상태입니다. 저는 낮은 자릿수부터 정렬을 할 거에요. 어떻게 할까요? 일단 1번째 원소부터 넣어봅시다. 일의 자릿수를 기준으로 넣겠다는 겁니다. 먼저 0의 1의자릿수는 0이니까 0번 버킷에 넣습니다.

그러면 버켓에 이렇게 들어간 상태입니다. 다음 수는 91인데, 이것의 1의 자릿수는 1입니다. 따라서 1번에 넣겠습니다.

그 다음에 오는 수는 21입니다. 역시 1의 자릿수가 1이니까 1번에 넣으면 되겠네요.
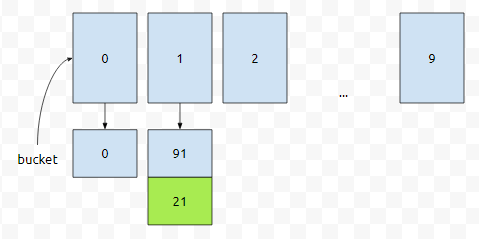
다음에 오는 수는 2입니다. 1의 자릿수가 2이므로, 2번에 넣겠습니다.

그러면 요렇게 들어갔을 겁니다. 이제 나오는 수는 9입니다. 1의 자리가 9이기 때문에 9번에 넣습니다.

이제 11도 넣어 봅시다.

그러면 이것을 차례대로 빼면, 1의 자릿수가 작은 순서에서 큰 순서로 빠지는 것일 겁니다. 그리고, 우선 순위가 같은 91과 21과 11을 보세요. 순서가 바뀌었나요? 앞에서부터 빼면 결코 바뀔 일이 없습니다. 일단 0번 버킷부터, 넣은 순서대로 빼 버렸다고 해 봅시다. 그러면 0이 먼저 빠지고, 91, 21, 11, 2, 9 순으로 빠질 겁니다.

보라색으로 칠한 부분은 91, 21, 11입니다. 넣기 전과 넣은 후 순서가 바뀌었나요? 아닙니다. stable 합니다. 왜 이 특성이 중요한지, 2회전을 돌려보면서 다시 이야기 하도록 하겠습니다.
이제 10의자리 수를 기준으로 버킷에 넣을 거에요.

먼저 0을 넣겠습니다. 10의 자릿수가 0이니까, 0번에 넣어야 할 거에요.

다음에 91은 십의 자리가 9이므로 9번에 넣습니다. 뭐가 바뀌었나요? 기준이 바뀌었습니다. 그 외에는 별 차이가 없습니다. 그냥 몇 번 상자에 들어가냐는 기본적인 원리는 똑같아요.

다음에 21은 10의자리가 2이므로, 2번에 넣어야 겠습니다. 마찬가지로 생각하면 11은 1번에 들어갈 거에요.
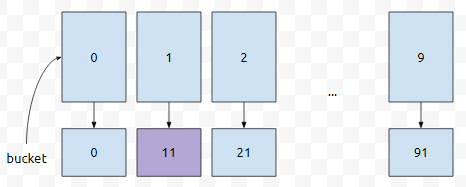
그런가요? 그러면 2와 9도 어디에 들어가야 할 지 눈치를 채실 수 있을 겁니다. 0번에 들어가야 합니다. 왜? 10보다 작은 수이기 때문입니다.

여기까지 넣어놓고, 또 버킷 0번부터 주루룩 돌면서 빼면 될 거에요. 그런데, 연두색 부분 보세요. 0, 2, 9. 이들은 1회전을 돌 때 이미, 정렬이 되어 있는 상태였어요. 1의 자릿수를 기준으로 오름차순으로. 만약에, 버킷에 넣을 때 순서가 바뀐다면 어떻게 될까요?
10의 자릿수에 대해서 오름차순이 될 지 몰라도, 1의 자릿수에 대해서는 뒤죽박죽일 거에요. 즉, 이전 정렬 기준에 대해서 우선순위가 낮은 순에서 높은 순으로 정렬했는데, 버켓에 넣은 과정에서 순서가 틀어져 버리면, 어떻게 될까요? 예를 들어 2, 0, 9 순서대로 들어갔다면요. 정렬이 되지 않을 거에요. 이미, n회전을 돈 경우, n번째 자리까지 보았을 때, 오름차순으로 정렬이 되었다는 겁니다. n+1회전을 돌 때, 우선순위는 n+1번째 자리의 숫자인데, n+1번째 자리까지 보았을 때 오름차순이 유지되려면, stable 하다는 게 전제로 깔려야 하지 않을까요? 그러면, 제가 개략적으로 설명한 알고리즘은, 왜 stable 할까요?

이것은 배열의 앞 부분부터 버킷에 순차적으로 넣기 때문에, 가능합니다. 그리고 뺄 때, 0번 버킷부터 뺄 거고, 버켓에서 원소를 뺄 때에는 x번 바구니에 있는 맨 앞의 원소부터 빼기 때문에 가능합니다.
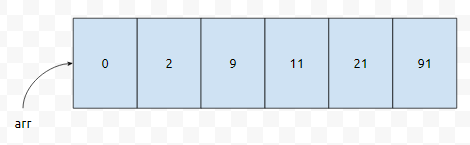
최종적인 정렬 결과는 아래와 같이 나옵니다.
이것은 b = 10일 때 sorting을 최대 2자릿수까지 나오는 데이터에 대해서, 2회전만에 정렬 했다는 겁니다. 만약에 수의 범위가 [0, 20억]이면 어떨까요? 20억을 10진법으로 표현하면 10자리가 나오는데, 그러면 10회전을 해야 합니다. 배열의 크기가 500만인 상황에서는 적절한 방법이 될 수 있을까요?
배열의 크기도 큰 상황에서, 바구니들을 생성하고, 거기에 넣었다 빼 버렸다가 clear 하는 작업을 10회. 물론, 누적 배열로 관리하면 그것 조차도 필요는 없겠다마는 딱 봐도 힘들어 보입니다.

이를 2회전으로 줄일 수 있는데요. 65536 진법을 이용하면 가능합니다. 65536^2이 20억보다는 크기 때문입니다. 20억 또한, 65536 진법으로 두자리로 표현할 수 있기 때문에, 하위 자리를 기준으로 한 번 돌리고, 상위 자리를 기준으로 또 한 번 돌리기만 하면 됩니다. 이것은 suffix array를 O(nlogn)에 구축하는 매우 중요한 기법이므로, 알아두시는 편도 나쁘지 않겠습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 최대공약수 최소공배수 알고리즘 : 짧은 코드 이해해 봅시다. (2) | 2019.08.07 |
|---|---|
| 약수 구하기 알고리즘 : n^0.5만 보고도 구할 수 있다. (6) | 2019.08.04 |
| 병합 정렬 : sorting 된 두 배열을 합치면서 해결한다. (4) | 2019.07.30 |
| 버블 정렬 알고리즘 : 인접한 원소들을 비교하면서 진행한다. (5) | 2019.07.23 |
| 부분합 구하기 : 누적합만 들고 있으면 된다. (8) | 2019.07.21 |


최근댓글