정렬 알고리즘 중, 버블 정렬은 서로 이웃한 원소들끼리 비교하면서 우선 순위가 낮은 데이터를 뒤로 보내는 정렬을 합니다. 이것도, insert, selection과 같이 시간 복잡도는 O(n^2)인데요. 따로 처리를 하지 않는 이상, 어떠한 경우에도, 제곱에 비례하기 때문에, merge나 heap에 비해서는 거의 안 쓰인다고 보시면 되어요.
배열 [2, 1, 4, 5, 3]을 오름차순으로 정렬해 볼 겁니다. 그러면 수가 작을수록 우선 순위가 높고, 수가 클수록 우선 순위가 낮다는 이야기가 되겠어요. 인접한 두 수 a와 b가 있다면, a보다 b가 더 작다면, a랑 b를 바꾸는 식으로 동작할 듯 싶습니다.
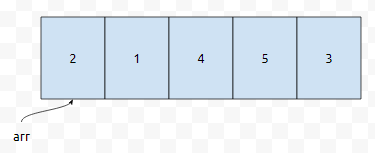
배열이 이렇게 있어요. 아직 sorting 하기 전이에요. 총 5회전을 돌 건데요. 이것은 1회전입니다.

먼저 초록색으로 칠한 부분을 봅시다. 앞에 있는 2가 1보다 크기 때문에, 두 원소를 바꿉니다.
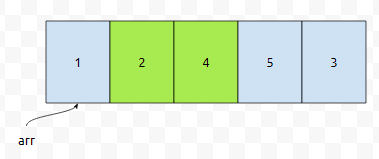
다음에 2번째와 3번째를 볼 건데요. 2는 4보다 작습니다. 순서에 맞게 배치되어 있기 때문에, 그냥 넘어갑시다.

3번째와 4번째도 봅시다. 이 때도 마찬가지에요. 4보다는 5가 크기 때문에, 순서에 맞게 되어 있어요. 넘어 갑시다.

4번째와 5번째를 봅시다. 그런데 5가 3보다 앞에 있네요. 순서에 맞지 않아요. 우선 순위가 낮은 게 더 앞에 있어요. 그렇기 때문에, 두 원소를 바꿉니다. 그러면 5와 3의 위치가 바뀌어서 3, 5가 될 거에요.

이렇게 1회전이 끝났습니다. 보라색으로 칠한 부분은, 더 이상 정렬할 필요가 없는 부분입니다. 파란색 부분을 보세요. 그것들 보다 보라색으로 칠한 것이 크거나 같음이 자명하기 때문이에요. 2회전 돌려 봅시다.

먼저 1번째와 2번째를 compare 합니다. 1이 2보다는 작아요. 순서에 맞게 배치 되었으니까 넘어갑니다.
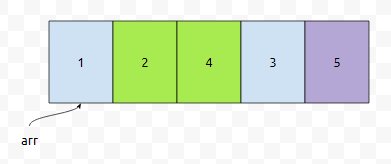
2번째와 3번째를 비교해 봐도 마찬가지인가요? 넘어갑시다.

3번째와 4번째를 보니까 이게 왠걸? 4가 3보다 앞에 왔어요. 순서가 맞지 않아요. 그러니까, 두 원소의 위치를 바꿉니다. 위치를 바꾸면 4와 3이 바뀌어서, 3, 4 순으로 올 겁니다.

그러면 비교가 끝납니다. 물론 계속 진행해도 되는데, 사실 4번째와 5번째를 compare 할 이유는 없을 겁니다. 왜냐하면, 이미 5번째는 4번째 원소보다 크거나 같은 것이 자명하기 때문이에요. 3회전 갑시다.

먼저 1번째와 2번째를 비교합시다. 순서 맞나요? 오름차순이니까 맞게 되어 있습니다. 넘어갑시다.

그 다음에 2번째와 3번째를 compare 합니다. 순서 맞나요? 네. 넘어갑시다.

3회전 끝났습니다. 3번째 것과 4번째 것을 왜 검사하지 않나요? 라고 물어보신다면, 2회전을 다 돌렸을 때, 1 ~ 3번째 원소보다 4 ~ 5번째 원소가 같거나 크기 때문입니다. 그리고 5번째 원소는 1 ~ 4번째 원소보다 크거나 같기 때문에, 역시 compare 할 필요가 없어요.

4회전 갑시다. 이건 그냥 1번째와 2번째만 비교하면 되는데요. 순서가 맞나요? 네. 건너 뜁시다.

4회전 끝났네요. 5회전은 더 할 필요도 없겠네요. 이런 식으로 인접한 친구들끼리 계속 검사하면서, 우선순위가 제일 낮은 원소를 뒤로 보내는 정렬을 버블 정렬이라 해요.
코드도 그렇게 복잡하지 않습니다.

보시면, j랑 j+1번째랑 비교하면서 swap을 하는 것을 볼 수 있어요. 인접한 것들끼리 비교하면서요. 바깥 for문은 몇 번째 회전인지, 그러니까 총 n번 돌아야 겠지요. 안쪽 for문은, 이미 뒤로 가서, 정렬된 부분 빼고 나머지 부분들 중에서 우선 순위가 가장 낮은 데이터를 뒤로 보내는 작업을 수행하고 있는 거에요. 특별한 처리를 하지 않는 한, 16번째 줄에 있는 비교 문장을 n^2/2회 가량 수행합니다. 효율적이지 못하다는 거에요.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 기수 정렬 (radix sort) : 버킷만 있으면 된다. (2) | 2019.08.02 |
|---|---|
| 병합 정렬 : sorting 된 두 배열을 합치면서 해결한다. (4) | 2019.07.30 |
| 부분합 구하기 : 누적합만 들고 있으면 된다. (8) | 2019.07.21 |
| 계수 정렬 (counting sort) : 특정 숫자의 빈도를 센다. (2) | 2019.07.20 |
| 이진 검색 (binary search) : 정렬이 되어 있어야 한다. (0) | 2019.07.19 |


최근댓글