(2차원) 배열에서 가장 큰 정사각형을 찾는 것은 dp로 해결할 수 있습니다. 문제를 조금 바꿔보겠습니다. 가장 큰 직사각형은 어떻게 구해야 할까요? 문제의 제한이 딱 하나 바뀌었을 뿐인데, 난이도는 4단계 정도 높아졌습니다. 이 문제를 보도록 하겠습니다.
문제를 요약하면 다음과 같습니다.

n이 범위는 1이상 2000 이하입니다. 시간 제한이 3초인 것을 감안했을 때, O(n^2)나 O(n^2logn) 정도에 풀어야 한다는 결론을 얻을 수 있습니다. 그런데, 후자는 생각보다 상수 줄이기가 빡빡하기도 하고 제가 시도해 본 방법이 아니므로, 저는 전자로 시도해 보겠습니다.
먼저 간단한 상식 아닌 상식을 통해서 관찰을 하나 해 보도록 하겠습니다.

길이가 3, 4, 2, 6인 높이 1짜리 직사각형이 있습니다. 대충 요래 있다고 생각해 봅시다. 그러면, 얘네들 안에 있는 길이 2, 높이 4짜리 직사각형은 만들 수 있나요?

네 있습니다. min(3, 4, 2, 6) = 2인데, 이것은 2보다 크거나 같기 때문입니다. 그런데 길이가 3, 높이가 4인 직사각형은 만들 수 없습니다. 이것은 왜 그럴까요?

min(3, 4, 2, 6) = 2는 3보다 크거나 같지 않기 때문입니다. 히스토램에서 가장 큰 직사각형과 비슷한 무언가를 본 거 같네요. 그러면, 우리는, 해당 위치부터 가로 방향을 볼 때, 0이 얼만큼 연속이 되어 있는지를 채워야 겠습니다. 이것이 제가 설명한 w값과 관련이 있기 때문입니다.

위에 배열은 인풋으로 들어온 것이고, 아래 배열은 해당 위치에서부터, 0이 얼만큼 연속이 되어 있는지를 나타냅니다. 여기까지는 간단하게 구현을 할 수 있다면 무난하게 해결하실 수 있습니다.
그러면, 채워진 데이터를 통해서 무엇을 봐야 할까요? 가로 길이를 고정시켰을 때, 높이의 최댓값을 구해야 함을 알 수 있습니다. 예를 들어 가로 길이가 2라고 해 보겠습니다.
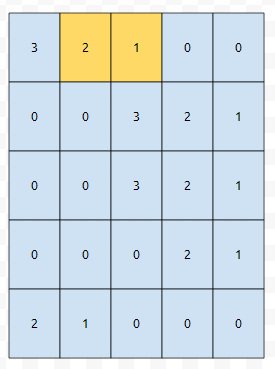
그러면 요래 선택할 수 있나요? 네. 이 값이 둘 다 0이 아니기 때문입니다.

그러면, 보라색부터 선택하고 노란색을 선택한 셈이니, 보라색을 대표 위치로 설정합시다. 그런데, 사실, 이것만 있는 게 아닙니다.
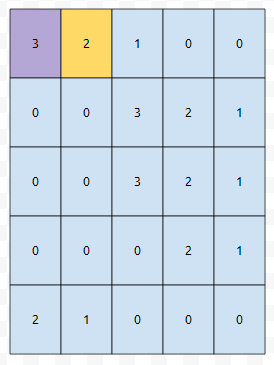
가로 길이가 2인 것을 선택할 수 있는 경우는, 요렇게도 선택할 수 있습니다. 3은 2보다는 크거나 같기 때문에, 요런 식으로도 선택할 수 있어요. 이것을 조금 더 관찰해 보면 아래와 같이 정리할 수 있습니다.

어찌되었던 보라색에서 출발하면, 가로 길이가 2인 직사각형을 선택할 수 있다. 이들의 공통점이 있습니다. 바로 2보다 크거나 같다는 점입니다. 이들을 가지고 무엇을 할 수 있는지는 모르겠습니다만, 우리는 관찰을 하나 더 할 수 있습니다. 가로의 길이가 1 이상인 직사각형을 선택할 때, 출발점이 될 수 있는 경우는, 아래와 같습니다.

즉, 이런 배열이 있을 때, arr[i][j]가 큰 위치부터 작은 위치까지 내림차순으로 순회해야 함을 볼 수 있습니다. x가 2보다 크거나 같은 집합이, x가 1보다 크거나 같은 집합에 속하기 때문입니다. 그러니, 정렬이 필요한데, 사실 2000 이하이므로 count sort를 응용하면 로그가 떼진 O(n^2)에 전처리가 가능합니다.
문제는, 순회를 하면서 집합이던 뭐에 추가가 될 거라는 겁니다. 그리고, 이 때 될 수 있는 높이 값들 중에서 제일 큰 값을 구해야 한다는 것입니다. 집합에 추가가 될 때마다, 될 수 있는 높이값들의 최대치를 구하는 것을 O(1)이나, O(logn)에 수행해야 한다는 이야기입니다. 일단, '될 수 있는 높이'에 대해서 먼저 생각해 보겠습니다.
가로 길이가 3일 때 부터 보겠습니다.

높이가 3인 경우를 만들 수 있나요? 그럴 수는 없습니다. 어떻게 하더라도요. 그런데, 높이가 2인 것은 만들 수 있습니다.

왜일까요? 세로 방향으로 읽어냈을 때, 3 이상의 수가 연속된 것이 두 개 이상 있는 경우가 있기 때문입니다. 2행 3열, 3행 3열. 이렇게 있습니다. 그러면 가로 길이가 2일 때에는 어떨까요?
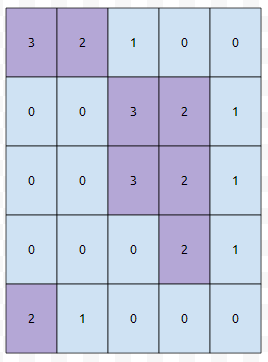
쭉 읽어보면, 높이가 3인 것까지 만들 수 있다는 것을 알 수 있습니다. 이는, 세로 방향으로 읽었을 때, 2 이상의 수가 최대 3번 연속이 되기 때문입니다.
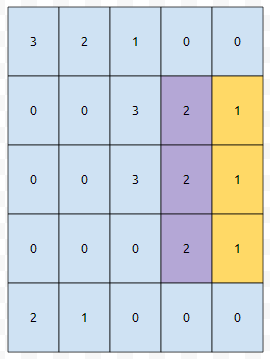
그러면, 최대로 연속한 x 이상의 수를 매 쿼리마다 어떻게 구할까요? 세그먼트 트리? 그런데, 사실 조금만 아이디어를 바꿔서 생각해 보면, 유니온 파인드로도 쉽게 구할 수 있음을 알 수 있습니다. 왜냐하면, 최댓값을 빼고 생각해 보면, 각 열에 집합 하나가 추가되면서, 특별한 경우에 집합 무언가와 합쳐지는데, 이 때 묶여져 있는 집합의 최대 크기를 구해라랑 같기 때문입니다.
묶는다. 찾는다. 부모를. 원소를. 추가 연산만 주어진다. 너무 유니온 파인드 같다는 겁니다.
이것을 구체화 시키면 아래와 같습니다.

각 열마다 parent 배열과 count 배열을 관리한다면, 다음과 같이 merge를 시킬 수 있습니다.

여기서 row는 row번째 열을 의미합니다. 그리고, merge를 호출하는 코드는 아래와 같습니다.

(x, y-1)과 (x, y+1)과 merge를 시도하는 코드입니다. 그리고 merge를 한 다음에 y의 부모의 cc값을 얻어오는데, 이 부분 역시 유니온 파인드를 잘 이해하셨다면 그리 어렵지 않게 코딩하실 수 있습니다. 이 문제를 통해, 유니온 파인드의 응용, 오프라인 쿼리를 어떻게 잘 쓰는지, 어떻게 해당 문제를 보고 관찰을 하는 지 배울 수 있었습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 백준 1060번 구간 : 후보해를 추린다. (0) | 2020.12.03 |
|---|---|
| 백준 소수인팰린드롬 : 팰린드롬인지 먼저 검사한다. (0) | 2020.11.12 |
| 백준 11003 최소값 찾기 : 큐와 덱를 응용해 봅시다. (0) | 2020.09.11 |
| 다익스트라 알고리즘 : 이미 결정된 노드의 인접 노드를 또 탐색하면 어떻게 될까요? (0) | 2020.08.11 |
| 슬라이딩 윈도우 알고리즘 : 2개의 커서가 중요하다. (2) | 2020.07.29 |


최근댓글