요새 코테 철이 되었습니다. 저도 간간히 구현력을 잃어버리지 않기 위해서 조금씩 복기만 하고 있습니다. 백준 11003번 문제는 최솟값을 구하는 문제입니다. 특정 구간 [e-k, e]에서의 최솟값을요. 단, 0보다 작은 위치의 구간은 무시하고 구해야 합니다. 별로 어렵지 않아 보이는데, 문제는 n이 500만입니다. 입력 받느라 시간이 많이 가는 건 흐음.
O(n)으로 줄일 수 있습니다. 다들 아시는 기법을 소개하도록 하겠습니다.
관찰을 해야 할 것은 2가지 상황입니다. 어떠한 데이터가 추가되는 상황하고, 제거되는 상황. i번째에 있는 데이터가 제거되면, 더 이상 추가되지 않는다는 것을 관찰하는 것 또한 포인트입니다. 현재, 이런 식으로 데이터가 들어갔다고 해 보겠습니다.
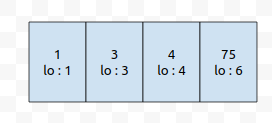
그리고 저는 7번째 위치에 있는 3이라는 데이터를 넣을 예정입니다. 우리에게 중요한 것은 구간의 최솟값입니다. 여기서, 우리는 왼쪽에서부터 오른쪽으로 훑을 건데요, 필요 없는 데이터를 골라내 보겠습니다.
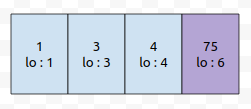
6번째 위치에 있는 75는 필요할까요? 아닙니다. 왜냐하면, 오른쪽으로 훑어 갈수록, 6번째 보다 7번째가 더 오래 살아남습니다. 게다가, 우리가 구하려는 최솟값이 우선순위가 더 높다면, 75보다는 3이 앞섭니다. 따라서, 75, 6번째 위치는 쓸모 없기 때문에 제거합니다.

이제 4, lo : 4를 보겠습니다. 역시 마찬가지입니다. 4보다는 3이 앞서고, 심지어 7번째 위치는 오른쪽으로 훑어간다면, 4번째 위치보다는 오래 살아남을 겁니다. 그러면, 이것 역시 제거를 해야 겠네요.

이제 3번째 위치에 있는 3은 어떤가요? 3과 3은 우선순위가 같습니다. 그러면 뭐가 더 오래 살아남을까요? lo가 3인 것보다는 7인 것이 더 오랫동안 자료구조에 있을 겁니다. 따라서, 3번째 위치에 있는 3을 제거합니다.

다음에 맨 뒤에 있는 것을 보았더니, 1번째 위치에 1이 있습니다. 이것을 제거하면 곤란하겠군요. 왜냐하면, 오래된 정보라고 해도, 1은 3보다 앞서기 때문에, 여전히 중요합니다. 우리가 구해야 하는 것은 구간의 '최솟값'이기 때문입니다. 따라서, 1번째 위치에 1이 있다는 정보 뒤에 7번째 위치에 3이 있다는 정보를 추가합니다.
여기까지 로직을 정리하면, 위치도 정렬이 되어 있고, 값 또한 오름차순으로 정렬이 된 경우에 k번째 위치에 C가 있다는 정보를 자료구조에 추가한다고 해 봅시다. 그럴 때, 자료구조가 비거나, 맨 뒤에 있는 값이 C보다 작지 않으면 계속 뒤에 있는 아이템을 뺍니다.
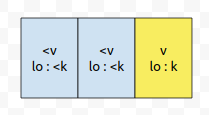
그러면, 위치가 k보다 작으면서, 값이 v보다 크거나 같은 것은 이미 다 빠진 상태입니다. 그러면 앞에 있는 것들은, 값이 v보다 작습니다. 하늘색으로 표시된 노드들은 k번째 위치 이전에 추가된 것이고, 하늘색 부분이 위치도 오름차로 정렬되어 있고, 값도 오름차로 정렬되어 있다면, 당연하게도, 노란색을 추가한 후에도 의도에 맞게 정렬이 될 겁니다.
왜냐하면, 하늘색 부분의 값은 v보다 작고, lo도 k보다 작기 때문입니다. 즉, 노란색이 추가 되기 전에 이미 추가가 되었습니다. 문제는, 삭제입니다. 삭제를 할 때에는 어떻게 하면 좋을까요? 간단합니다. 앞에서부터 제거해 나가면 됩니다.

자료구조에 이런 것들이 들어가 있습니다. 만약에, 현재 [3, 7] 구간만을 보아야 한다면 어떨까요? 이 시점에서는 앞에서부터 제거해 나가면 되는데요.

lo가 1입니다. 우리가 봐야 할 구간은 3부터입니다. vaild 하지 않으니, 제거합니다.
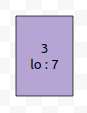
이것은 어떤가요? 7번째 위치는 고려해야 할 구간입니다. 따라서, 이것은 제거하지 않습니다. 제가 말한 부분을 그대로 코드로 구현해 보겠습니다.

deque를 쓸 수도 있지만, 저는 배열로 큐를 만들어 보겠습니다. 물론, 원소들은 많아봤자 500만개 이상 들어가지 않으므로, 선형큐 대신에, 원형 큐로 구현하셔도 무난합니다. 넉넉하게 1<<23개 정도 저장하면 되겠네요.

인덱스들을 제거할 때에는 s가 증가하고, 데이터를 추가하기 위해서, 뒤에서부터 제거할 때에는 e가 감소합니다. 이 부분만 잘 챙겨가셔도 무난할 듯 싶은데, 복잡도가 어떻게 될까요? 간단하게 생각해 봅시다. 47에서 48번째 줄만 보겠습니다. 이 while loop가 계속 수행이 되면, 원소가 제거됩니다. 원소는 최대 몇 번 제거가 될까요? 1번 제거됩니다. 왜 그럴까요? 오른쪽 방향으로 포인터가 움직이기 때문입니다.
47번째 줄을 보면 앞에서 제거됩니다. 이것은 그냥 범위가 넘어가서 제거가 되는 것입니다. i-L보다 작거나 같았기 때문에요. 이 때, i가 추가된 상황입니다. 계속 오른쪽으로 훑기 때문에, i-L보다 작은 위치가 자료구조에 추가될 일은 없습니다. 문제는 48번째 줄인데, 이것도 쉽게 생각해 보겠습니다.
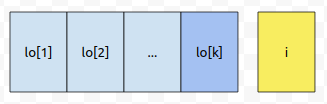
i번째 위치가 추가되고 있을 때 상황입니다. loop를 한 번 돌 때 마다 해당 위치에 대한 정보가 추가됩니다. 이 위치는 루프를 돌 때 마다, 계속 증가하지, 감소하지 않습니다. 그러면, 그림에서 lo[k]는 i보다 작습니다. 왜냐하면, 이전에 추가 되었기 때문입니다. 그러면, i보다 작은 위치가 i는 계속 증가하는데, 추가될 일이 있을까요? 그렇지는 않습니다.
따라서, 삭제 횟수의 합은 최대 O(n)입니다. n은 배열에 있는 원소의 갯수라고 하면요. 따라서, 시간 복잡도는 O(n)이 됩니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 백준 소수인팰린드롬 : 팰린드롬인지 먼저 검사한다. (0) | 2020.11.12 |
|---|---|
| 배열에서 가장 큰 직사각형 구하기 : 관찰을 통해 풀어봅시다. (2) | 2020.10.18 |
| 다익스트라 알고리즘 : 이미 결정된 노드의 인접 노드를 또 탐색하면 어떻게 될까요? (0) | 2020.08.11 |
| 슬라이딩 윈도우 알고리즘 : 2개의 커서가 중요하다. (2) | 2020.07.29 |
| amortized 복잡도 : average complexity와 뭐가 다른가요? (2) | 2020.07.16 |


최근댓글