귀납법은 이산 수학 시간에 들어보셨을 증명 방법입니다. 어떻게 쓰는지, 백준에 있는 문제를 풀어보도록 하겠습니다. 최근 USACO 실버에 나온 문제라고 하는데, 실버 같지 않습니다.
문제를 요약하면, 길이가 n인 순열이 주어집니다. 1부터 n까지의 수가 1번 등장합니다. 그리고 m개의 웜홀 정보가 (a, b, c)로 주어지는데, 너비가 c인 웜홀을 열면 a번째 원소와 b번째 원소를 바꿀 수 있다는 의미입니다. 어떻게 잘 배치해서 순열을 오름차순으로 정렬하려고 할 때, 연 웜홀들의 최소 너비를 최대화 시키는 문제입니다.
이걸 보면, 일단 이분 탐색임을 알 수 있는데, 정렬이 되어야 하는 조건이 상당히 어렵습니다. 어떻게 해 볼 것인가. 작은 집합부터 보면서, 큰 집합에서 성립하는지 보아야 겠습니다. 귀납법은 아래와 같은 플로우를 가지고 있습니다.

먼저 작은 경우에 대해서 보이고, 일반화를 시킬 겁니다. 여기서 P(x)는 1, 2, ... , x가 웜홀들에 의해서 하나의 집합이 되었을 때, 1번부터 x번까지 배치할 수 있는 가짓수는 x!이다. 즉, [1, 3, 2, ..., x] 이렇게 배치할 수도 있고, [x, x-1, 3, 2 ...] 이렇게 배치할 수도 있다는 의미입니다. 이 말은 크기가 x인 임의의 순열을 일련의 연산들을 통해서 정렬할 수 있다는 이야기도 됩니다.

먼저, 1과 2를 바꿀 수 있는 웜홀이 열렸다고 해 보겠습니다. 1, 2만 있는 순열이 있다고 생각해 보겠습니다. 1과 2를 바꿀 수 있다면, [1, 2]가 되거나, [2, 1]이 될 수 있습니다. 길이가 2인 순열의 갯수는 2!입니다. 2!은 2이므로, P(2)에 대해서 성립합니다.
P(n)에 대해서 성립한다고 가정합시다. P(n+1)은 성립할까요?

n+1이 1, ... , n 중에서 어떤 노드와 연결이 되었다고 해 보겠습니다. 즉, a는 [1,n]에 속한 정수입니다. 처음에 순열이 [1, 2, ... , n+1] 요렇게 있었다고 해 보겠습니다. 그리고 편의상 a는 n이였다고 해 봅시다.

n+1이 자리를 안 바꿨다고 해 보겠습니다. 그러면 군청색 친구들끼리 어떻게 자리를 잘 바꿀 수 있을 겁니다. P(n)이 성립하기 때문입니다. 군청색 친구들끼리 자리를 잘 바꿔서 순열을 만드는 가짓수는 n!입니다.
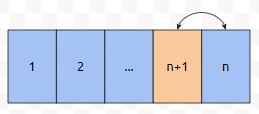
n과 n+1이 원래 순열에서 자리를 맞 바꿨습니다. 이 때에는 어떨까요? n+1은 n을 제외하고 자리를 맞바꾸지는 못하지만, 군청색으로 칠한 원소들은 알아서 잘 바꿀 수 있습니다. P(n)이 성립하기 때문입니다. 그 가짓수는 n!입니다. 여기까지는 어렵지 않습니다. 문제는, n+1이 임의의 자리로 갈 수 있느냐입니다.

그런데, 이 질문을 돌려 말하면, [1 ... n]과 [n+1] 이렇게 두 부분으로 나누었을 때, n이 [1 ... n]으로 이루어진 순열에서 임의의 위치로 갈 수 있다면, n+1도 길이 n+1의 순열에서 임의의 위치로 이동할 수 있습니다. 예를 들자면 n이 1번 위치로 이동했다 해 보겠습니다.
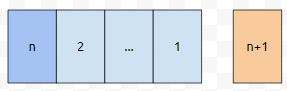
이것은 가능합니다. P(n)이 성립하기 때문입니다. 이 상태에서 맨 뒤에 있는 n+1과 교환을 시도할 수 있습니다.

이것은 가능합니다.

그러므로, 일련의 연산에 의해서 n+1은 1번째 위치로 갈 수 있고, 군청색 영역끼리 잘 지지고 볶을 수 있습니다. 군청색 영역끼리 볶는 가짓수는 n!입니다. 그러면 n+1이 2번째, 3번째, ... , n번째로 오는 것도 가능할까요? 마찬가지로 [1 ... n] 순열에서 n을 a번째로만 옮겨놓고, a번째에 있는 n과 맨 뒤에 있는 n+1을 옮겨놓기만 하면 n+1이 a번째로 갈 겁니다. 그리고, 이 상황은 주황색이 하나 있고, n!개의 순열이 만들어지는 군청색 영역으로 나뉘게 됩니다.
전체 가짓수는 (n+1)!이 됩니다. a가 n이나 1이 아니여도 마찬가지일까요?
이 경우도 마찬가지로 생각하시면 됩니다.
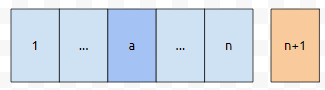
먼저 a를 n+1이 가려고 하는 위치에 옮겨 놓습니다. 예를 들어 1번째 위치로 옮겨놓아야 한다고 해 보겠습니다.
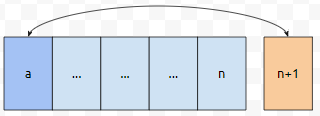
그러면, 일단 a를 1번째 위치로 옮겨 놓습니다. 다음에, n+1과 a를 맞바꾸면 됩니다.
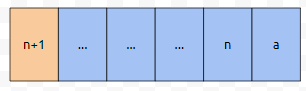
즉, n+1도 임의의 위치에 가져다 놓을 수 있고, 가져다 놓았을 때 군청색 영역 n개에 대해서도 각각의 순열이 만들어 지므로, 가짓수는 (n+1)n! = (n+1)!이 됩니다. 즉, P(n)이 성립하면, P(n+1)도 성립함을 알 수 있습니다. 이제 문제의 예제를 보겠습니다.

[3, 2, 1, 4]로 주어진 배열을 오름차순으로 정렬하기 위해서는 1과 3을 바꿔야 함을 알 수 있습니다. 여기서, 1과 3이 어떻게든 변경이 되어야 하므로, 이 둘을 한 묶음으로 퉁칠 수 있습니다. 귀납법으로 보인 것을 생각해 보았을 때, 1과 3이 하나의 집합에 묶여져 있다면, 정렬이 가능함을 알 수 있습니다.
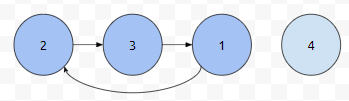
이 경우에는 2, 3, 1이 한꺼번에 자리를 옮겨야 하므로, 1과 2와 3이 하나의 집합에 묶여져 있다면 파란색 부분은 정렬이 가능함을 알 수 있습니다. 만약에 하나의 집합으로 이루어져 있지 않으면 어떻게 될까요?

1이 원하는 목적지로 갈 수 없음을 너무 쉽게 알 수 있습니다. 이 관찰을 하면, 정렬이 되기 위한 최소 필요 조건을 도출할 수 있고, x 이상인 웜홀들만 넣었을 때 최소 필요 조건을 만족하는지를 유니온 파인드로 알아낼 수 있습니다.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 많이 언급되는 오프라인 쿼리 간단하게 훑어봅시다. (0) | 2021.01.04 |
|---|---|
| 정점 분할 : 노드를 상태에 따라 여러 개로 쪼갠다. (2) | 2020.12.29 |
| 백준 1060번 구간 : 후보해를 추린다. (0) | 2020.12.03 |
| 백준 소수인팰린드롬 : 팰린드롬인지 먼저 검사한다. (0) | 2020.11.12 |
| 배열에서 가장 큰 직사각형 구하기 : 관찰을 통해 풀어봅시다. (2) | 2020.10.18 |


최근댓글