안녕하세요. 백준 chogahui05입니다. 플로이드 알고리즘은, 알고리즘 수업 시간에 많이 배우실 거에요. 음의 사이클이 없는 경우에, 이 알고리즘이 어떻게 동작하는지 알아보도록 하겠습니다.

이 코드는 몇 줄 안 되니 외우시는 분들도 많으실 거라 생각이 듭니다만. 그래도 보도록 하겠습니다. 9번째 줄의 for loop를 보면 n번 loop를 돌린다는 것을 알 수 있어요. 다음에 11번째 줄에 있는 for loop, 13번째 줄에 있는 for loop, 15번째 줄에 있는 if문 안을 보시면, 조건이 맞으면 dist[i][j]를 업데이트 한다는 것을 알 수 있어요.
음의 사이클이 없다면, a에서 a로 오는 비용은 0보다 크거나 같습니다. 따라서, 같은 장소를 2번 이상 방문하는 것은 손해라는 것을 알 수 있습니다. 일단, 이 부분 먼저 체크하고 지나가도록 하겠습니다.
위에 9번째 for문에서 k라는 값이 있어요. k값이 증가할 때 마다, 저는 정보를 업데이트를 했다고 표현하겠습니다.

예를 들어, 정보가 업데이트 되지 않았다면, from에서 to로 이동할 수 있다면, from에서 to를 잇는 간선의 cost가, from하고 to가 같다면 0이, 이동할 수 없다면 inf 값을 가질 겁니다. 그러면 k가 0부터 n-1까지 도는 동안에 어떤 일이 일어나는지 관찰해 보도록 하겠습니다. k가 0인 경우에, 추가로 고려되는 부분은 어떤 것일까요?
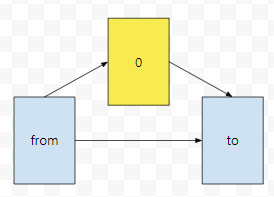
0을 거쳐서 갔거나, 아니면 그냥 갔거나입니다. 그러면, 우리는 from에서 to까지 직접 가는 경우와, 0번을 거쳐서 가는 경우, 이렇게 2가지로 나누어서 생각할 수 있어요. 사실 from에서 to까지 많아 봐야 2개의 간선을 거쳐서 가는 경우는, 이 둘 밖에 없다는 것을 알 수 있어요.
다음에 k = 1이 되었다고 생각해 봅시다. 그러면 기존에 알려졌던 경로 뿐만이 아니라, from에서 1로 간 다음에 1에서 to로 가는 경우까지 고려를 하는데요. 그런데, 이 때, from에서 1로 가는 경로나, 1에서 to로 가는 경로는 어느 경우까지 고려가 되었나요? 0을 거쳐서 갔느냐. 그렇지 않았느냐 또한 고려가 되었습니다.

그러면 from에서 to까지 가는 경로 중에서 고려되는 수는 다음과 같을 거에요. 1을 고려하지 않고 from에서 to로 바로 갔을 때. 1을 중간에 거쳐서 갔을 때. 즉, dist[from][to]와 dist[from][1]과 dist[1][to]는 0을 거쳐서 간 경우와 그렇지 않은 경우를 cover를 했었고, 그에 따라서 업데이트 된 정보는 from에서 to까지 {0,1} 중에서 적절히 잘 선택해서 간 모든 경로 중 최소치를 택했다고 볼 수 있어요.
그러면, 이것을 k = t일 때 확장을 시켜 봅시다.

이 경우는, 어떤 경우가 모두 고려될까요? 간단합니다.

k = t일 때 생각해 봅시다. 그러면 dist[from][to]는 from에서 {0, ... , t-1}을 잘 거쳐서 to로 가거나, 막바로 to로 가는 모든 경우 중에서 최소 거리를 cover 합니다. 그리고 dist[from][t]는 from에서 {0, ... , t-1}을 잘 거쳐서 t로 가거나막바로 t로 가는 모든 경우 중에서 최소 거리를 cover 합니다. 그리고 마지막 값인 dist[t][to]는 t에서 {0, ... , t-1}을 잘 거쳐서 가거나, 막바로 to로 가는 모든 경우 중에서 최소 거리를 cover 합니다.
그러면 from에서 {0,...,t}를 잘 거쳐서 to로 가는 최단 거리는 어떻게 구하면 될까요? 똑같습니다. 만약에 from에서 다음과 같이 가는 경로가 최적이였다고 해 봅시다.

t값이 10일 때 dist[i][j] 값들의 업데이트가 끝났다고 해 봅시다. {0, ... , 10} 까지의 경유지들을 잘 선택해서 from에서 to까지 가는 최소 거리가 위와 같다고 해 봅시다. 그러면, 이 때에는 10을 안 거쳐도 됩니다. 이는 {0, ... , 9}에 있는 경유지들을 잘 선택해서 from에서 to까지 가는 경우입니다. 이 경우는 그냥 기존에 있었던 dist[from][to]의 값을 그대로 썼을 겁니다.

만약에 from - 1 - 3 - 10 - 4 - to로 가는 게 최적이였다면 어떨까요? 그렇다면, from에서 {0, ..., 9}에 있는 경유지들을 잘 선택해서 10으로 가는 case A, 막바로 10으로 간 경우, 그리고 10에서 {0,...,9}에 있는 경유지들을 잘 선택해서 to로 가거나, to로 바로 가는 case B로 나눌 수 있는데요. case A는 dist[from][10]이, case B는 dist[10][to]가 cover를 하고 있었습니다.
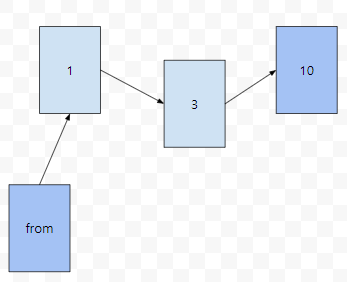
from에서 10을 봤을 때, {0,..,9}까지의 경유지 중 몇 개를 적절히 잘 선택해서 간 최단 경로였습니다.

다음에, 10 - 4 - to로 이어지는 경로도, {0,...,9}까지의 경유지 중에서 몇 개를 적절히 잘 선택해서 가는 경로 중 하나였습니다. 이 둘은 dist[from][10]과 dist[10][to]가 cover 하고 있는 값이였다는 것이 핵심입니다. 즉, k = t일 때, 업데이트가 끝나면 from에서 {0,...,t}까지의 경유지 중에서 적절히 몇 개를 선택해서, from에서 to까지 가는 모든 경로들을 모두 고려한다고 말을 할 수 있어요.
여기서 의문점이 몇 가지 들 수 있습니다.

10에서 to로 가는 최단 거리가 실제로 3을 거쳐서 가고, from에서 10을 가는 최단 경로도 3을 거쳐서 가는 경우에는 어떻게 되느냐. 그런데, 잘 보면, 이 경우는 3에서 바로 direct로 3으로 꽂아주면, 최단거리가 됨을 알 수 있어요.
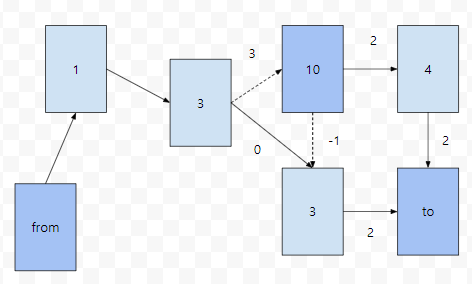
이 경우, from에서 to까지의 최단거리가 dist[from][10] + dist[10][to]가 아닙니다. 즉, 이 때, dist[from][to]는 from에서 10을 거쳐서 to로 가는 경우를 고려하지 않아도 된다는 소리입니다. 그리고 그 경우는 dist[from][to]가 이미 커버하고 있었습니다. 물론, 10에서 3까지의 거리가 -20인 경우에는 이야기가 달라질 지도 모르겠어요. 그런데 이 때에는 음의 사이클이 있습니다. 음의 사이클이 없다고 가정했으므로 모순입니다.
from에서 to까지 가는 최단 경로는 어떻게 복원할까요? 이 질문은 솔직히 어려워 보이는군요. 이것은 플로이드가 어떻게 동작하는지를 잘 생각해보면, 생각보다 쉽게 간파하실 수 있습니다. 예를 들어서, from에서 to까지의 유일한 최단 경로가 다음과 같았다고 해 봅시다.
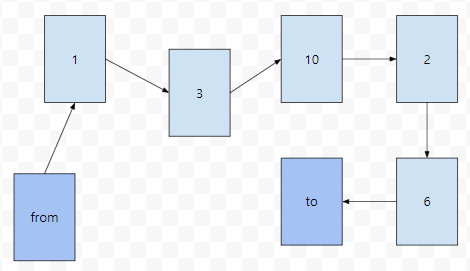
그러면 이것을 어떻게 추적할까요?

from에서 1까지 가는 것은 별 문제 없어요. 그런데 1에서 to로 가는 경로는, 어떻게 해석해야 하나요? 만약에 from에서 to로 가는 경로가 k = 1일 때 마지막으로 업데이트가 되었다고 하면, 1에서 3, 10, 2, 6을 거쳐서 간 경로가 최솟값이다. 라는 정보가 들어가 있으면 안 됩니다.
0을 거치거나, 거치지 않은 경우만 들어가 있어야 합니다. 즉, 경유지가 {0}이 있을 때, 이들을 적절히 잘 선택해서 1에서 to로 가는 최단 거리를 만들 수 없어요. 3, 10, 2, 6을 거쳐야 하기 때문이에요.

k값이 3일 때, dist[from][to]가 마지막으로 업데이트 되었다면 어떨까요? 이 경우에 from에서 3으로 가는 경로에도, 3에서 to로 가는 경로에도 0, 1, 2 셋 중 하나만 들어와야 할 겁니다. 그런데 3에서 to로 가는 경로에 10이 들어가 있어요.
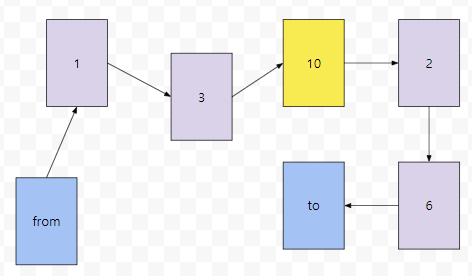
그러면 k값이 10일 때 from에서 to까지 가는 최단 경로가 마지막으로 업데이트 되었을까요? 네. 왜냐하면, 이 때에는 dist[10][to]가 10에서 {0, .. , 9} 중에서 몇 개를 잘 선택해서 to까지 가는 최단 경로도 저장하고 있었고, dist[from][10]이 from에서 {0, .. , 9} 중에서 몇 개를 잘 선택해서 10으로 가는 최단 경로도 저장하고 있었기 때문입니다.
그러면 10을 기준으로 다시 탐색해 나가시면 됩니다.

wif[i][j]의 값은 무엇을 의미하는지 잘 와닿지는 않습니다. 다만, dist[i][k] + dist[k][j]가 dist[i][j]보다 작을 때 특정 값으로 업데이트가 되는데요. 이 때, i에서 j로 가는 최단 경로는 k를 거쳐서 가는 것이 자명하기 때문에, wif[i][j]를 k로 업데이트 합니다. 그러면, i에서 j까지 최단 경로로 가려면 j를 거쳐야 한다는 정보를 얻을 수 있습니다.

이 정보를 얻었다면, s에서 e로 가는 최단 경로를 복원할 때, wif[s][e]의 값에 따라서 복원하시면 됩니다. 처음에 wif 배열의 모든 값이 -1로 초기화가 되어 있다면, wif[s][e]가 -1일 때 s에서 e까지 가는 경로가 있다고 정보를 어딘가에 출력한 다음에 return 문으로 빠져나오면 되겠네요.
'자료알고 > 알고리즘' 카테고리의 다른 글
| 항등식으로 구현체를 외울 수 있는 확장 유클리드 알고리즘 (2) | 2020.04.09 |
|---|---|
| 백준 공유기 설치 : 왜 이분탐색이 가능한가? (0) | 2020.03.27 |
| 백준 화성지도 : 구간에 장벽을 세운다. (5) | 2020.02.24 |
| 좌표 압축 알고리즘 : 범위가 클 때 어떻게 공간을 줄일까요? (4) | 2020.02.22 |
| 백준 balanced cow subsets : 반으로 잘 쪼개 봅시다. (6) | 2020.02.10 |


최근댓글